数据结构与算法
| 对象 | ————————> | 操作 |
|---|---|---|
| 线性表 | ————————> | 创建 |
| 遍历 | ||
| 插入 | ||
| 删除 | ||
| 查询 | ||
| 栈 | ————————> | 进栈 |
| 出栈 | ||
| 队列 | 插入 | |
| 树 | 删除 | |
| 图 | 查询 |
栈的操作
用一个素组实现栈
1.顺序栈元素"入栈"
最初，栈是"空栈"，即数组是空的，top 值为初始值 -1：
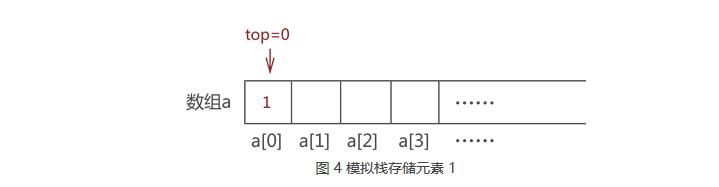
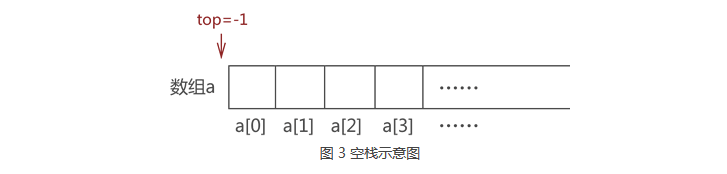我们默认数组下标为 0 一端表示栈底：
依次存储元素 2、3 和 4，最终，top 值变为 3：
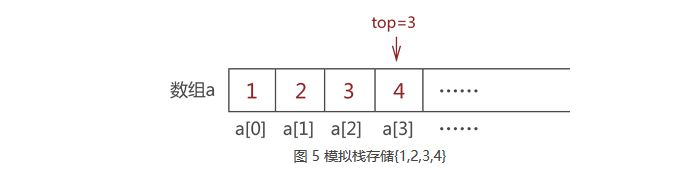
2.顺序栈元素"出栈"
将图 5中的元素 2 出栈，则需要先将元素 4 和元素 3 依次出栈。需要注意的是，当有数据出栈时，要将 top 做 -1 操作。
eg:实现进栈和出栈：
#include <stdio.h>
//元素elem进栈
int push(int* a,int top,int elem){
a[++top]=elem;
return top;
}
//数据元素出栈
int pop(int * a,int top){
if (top==-1) {
printf("空栈");
return -1;
}
printf("弹栈元素：%d\n",a[top]);
top--;
return top;
}
int main() {
int a[100];//创建一个数组作为栈
int top=-1;//初始为-1，然后++top就是从0开始的了
top=push(a, top, 1);
top=push(a, top, 2);
top=push(a, top, 3);
top=push(a, top, 4);
top=pop(a, top);
top=pop(a, top);
top=pop(a, top);
top=pop(a, top);
top=pop(a, top);
return 0;
}
程序的输出结果为：
队列的操作
1.顺序队列简单实现
入队和出队
顺序队列的缺点：
序队列之前的数组存储空间将无法再被使用，造成了空间浪费；
如果顺序表申请的空间不足够大，则直接造成程序中数组 a 溢出，产生溢出错误；
eg: 顺序表，C 语言实现顺序队列
#include <stdio.h>
int enQueue(int *a,int rear,int data){
a[rear]=data;
rear++;
return rear;
}
void deQueue(int *a,int front,int rear){
//如果 front==rear，表示队列为空
while (front!=rear) {
printf("出队元素：%d\n",a[front]);
front++;
}
}
int main() {
int a[100];
int front,rear;
//设置队头指针和队尾指针，当队列中没有元素时，队头和队尾指向同一块地址
front=rear=0;
//入队
rear=enQueue(a, rear, 1);
rear=enQueue(a, rear, 2);
rear=enQueue(a, rear, 3);
rear=enQueue(a, rear, 4);
//出队
deQueue(a, front, rear);
return 0;
}
2.环状顺序队列实现
优点：
使用此方法需要注意的是，顺序队列在判断数组是否已满时，出现下面情况：
- 当队列为空时，队列的头指针=队列的尾指针；
- 当数组满员时，(队列的头指针+1)=队列的尾指针；
（rear+1)%max==front，牺牲一个存储空间作为判定条件）
eg:实现环状顺序队列
#include <stdio.h>
#define max 5//表示顺序表申请的空间大小
int enQueue(int *a,int front,int rear,int data){
//添加判断语句，如果rear超过max，则直接将其从a[0]重新开始存储，如果rear+1和front重合，则表示数组已满
if ((rear+1)%max==front) {
printf("空间已满");
return rear;
}
a[rear%max]=data;
rear++;
return rear;
}
int deQueue(int *a,int front,int rear){
//如果front==rear，表示队列为空
if(front==rear%max) {
printf("队列为空");
return front;
}
printf("%d ",a[front]);
//front不再直接 +1，而是+1后同max进行比较，如果=max，则直接跳转到 a[0]
front=(front+1)%max;
return front;
}
int main() {
int a[max];
int front,rear;
//设置队头指针和队尾指针，当队列中没有元素时，队头和队尾指向同一块地址
front=rear=0;
//入队
rear=enQueue(a,front,rear, 1);
rear=enQueue(a,front,rear, 2);
rear=enQueue(a,front,rear, 3);
rear=enQueue(a,front,rear, 4);
//出队
front=deQueue(a, front, rear);
//再入队
rear=enQueue(a,front,rear, 5);
//再出队
front=deQueue(a, front, rear);
//再入队
rear=enQueue(a,front,rear, 6);
//再出队
front=deQueue(a, front, rear);
front=deQueue(a, front, rear);
front=deQueue(a, front, rear);
front=deQueue(a, front, rear);
return 0;
}
3.链式队列及基本操作
链式队列的结构：
链式队列数据入队：
链式队列数据出队：
eg:链式队列入队和出队
#include <stdio.h>
#include <stdlib.h>
//链表中的节点结构
typedef struct QNode{
int data;
struct QNode * next;
}QNode;
//创建链式队列的函数
QNode * initQueue(){
//创建一个头节点
QNode * queue=(QNode*)malloc(sizeof(QNode));
//对头节点进行初始化
queue->next=NULL;
return queue;
}
QNode* enQueue(QNode * rear,int data){
//1、用节点包裹入队元素
QNode * enElem=(QNode*)malloc(sizeof(QNode));
enElem->data=data;
enElem->next=NULL;
//使用尾插法向链队列中添加数据元素
//2、新节点与rear节点建立逻辑关系
rear->next=enElem;
rear=enElem;
//返回新的rear，为后续新元素入队做准备
return rear;
}
QNode* DeQueue(QNode * top,QNode * rear){
if (top->next==NULL) {
printf("\n队列为空");
return rear;
}
QNode * p=top->next;
printf("%d ",p->data);
top->next=p->next;
if (rear==p) {
rear=top;
}
free(p);
return rear;
}
int main() {
QNode * queue,*top,*rear;
queue=top=rear=initQueue();//创建头结点
//向链队列中添加结点，使用尾插法添加的同时，队尾指针需要指向链表的最后一个元素
rear=enQueue(rear, 1);
rear=enQueue(rear, 2);
rear=enQueue(rear, 3);
rear=enQueue(rear, 4);
//入队完成，所有数据元素开始出队列
rear=DeQueue(top, rear);
rear=DeQueue(top, rear);
rear=DeQueue(top, rear);
rear=DeQueue(top, rear);
rear=DeQueue(top, rear);
return 0;
}
树
| 树的分类 |
|---|
| 普通树（节点数目可以为0，1，2，3） |
| 二叉树（节点数目可以为0，1，2） |
| 完全二叉树（最后一行节点需要从左到右） |
| 满二叉树（节点的数目为2） |
| 树的表示 | ~ |
|---|---|
| 双亲表示法 | （顺序数组） |
| 孩子表示法 | （顺序表+链表） |
| 双亲孩子表示法 | （顺序表+顺序表+链表） |
| 孩子兄弟表示法 |
| 树的遍历 |
|---|
| 先序遍历 |
| 中序遍历 |
| 后序遍历 |
树的性质：树的节点+树的深度（高）+树的度
二叉树的性质：
1.二叉树中，第 i 层最多有 2i-1 个结点。（第一层只有一个根节点）
2.如果二叉树的深度为 h，那么此二叉树最多有 2h-1 个结点。（第一层只有一个根节点）
3.二叉树中，终端结点数（叶子结点数）为 n0，度为 2 的结点数为 n2，则 n0=n2+1。（叶节点的数量=度为2的数量+1（根节点数量））
(除了度为 0 的叶子结点和度为 2 的结点，剩下的就是度为 1 的结点（设为 n1），那么总结点 n=n0+n1+n2。)
图
图（有向，无向，带权（网））
| 图的分类 | ~ |
|---|---|
| 完全图 | 图中各个顶点都与除自身外的其他顶点有关系（一点发散到各个点） |
| 连通图 | 各个节点都是连接通的图 |
完全图：具有 n 个顶点的完全图，图中边的数量为 n(n-1)/2；而对于具有 n 个顶点的有向完全图，图中弧的数量为 n(n-1)。
浙公网安备 33010602011771号