Applese 走方格
【题目描述】
精通程序设计的 Applese 又写了一个游戏。
在这个游戏中,它位于一个 n 行 m 列的方阵中的左上角(坐标为(0, 0),行的序号为 0∼n−1,列的序号为 0∼m−1)。
现在它想不重复地走过所有格子(除了起点),最后回到左上角的一个方案。
每次只能往上下左右其中一个方向走一格。
【输入描述】
仅一行两个整数 n 和 m,表示方阵的大小。保证大于1×1。
1≤n,m≤10
【输出描述】
如果存在方案,则输出一行操作,包含"L"、"R"、"U"、"D",分别表示左、右、上、下。如果有多种方案,输出任意一种即可。
如果没有方案,则在一行中输出"-1"。【样例】
示例1
输入
2 2
输出
RDLU示例2
输入
2 3
输出
RRDLLU
思路:
首先奇数行奇数列时一定无解,其次注意边界数据 1 行 2 列与 2 行 1 列,然后进行搜索即可,搜索时注意存储方向,最后输出即可
除搜索外,还可以分类讨论 n、m 的奇偶进行构造,除奇奇的情况外,奇偶、偶奇、偶偶大致照下图进行构造
奇数行偶数列: ,偶数行奇数列:
,偶数行奇数列: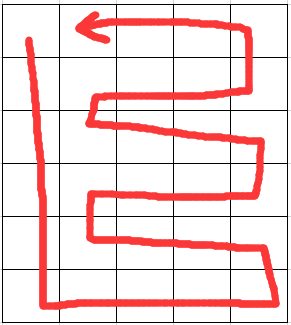 ,偶数行偶数列:
,偶数行偶数列: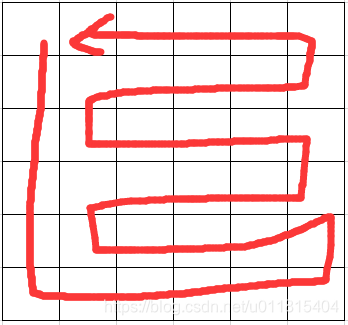
由于 n、m 均小于 10,因此除搜索、构造外,还可以打表,从 1*1 到 10*10 的 100 种情况都打成表,然后输出。。。
【源代码】
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
#define PI acos(-1.0)
#define E 1e-6
#define MOD 1000000007
#define INF 0x3f3f3f3f
#define N 1001
#define LL long long
using namespace std;
int n,m;
int cnt;
int path[N];
bool flag;
bool vis[N][N];
int dx[]={0,1,0,-1};
int dy[]={1,0,-1,0};
void dfs(int x,int y){
if(flag)
return;
if(x==1&&y==1&&cnt==n*m){//输出路径
for(int i=0;i<n*m; i++){
switch(path[i]){
case 0:cout<<"D";break;
case 1:cout<<"R";break;
case 2:cout<<"U";break;
case 3:cout<<"L";break;
}
}
cout<<endl;
flag=true;
return;
}
for(int i=0;i<4;i++){
int nx=x+dx[i];
int ny=y+dy[i];
if(nx>=1&&nx<=m&&ny>=1&&ny<=n&&!vis[nx][ny]){
vis[nx][ny]=true;
path[cnt]=i;//存路径
cnt++;
dfs(nx,ny);
cnt--;
vis[nx][ny]=false;
}
}
}
int main(){
cin>>n>>m;
if(n%2==1&&m%2==1)//特判
cout<<-1<<endl;
else{
cnt=0;
flag=false;
dfs(1,1);
if(!flag)
cout<<-1<<endl;
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号