DAG 图判定(51Nod-2143)
题目
DAG图是指有向无环图,所谓有向无环图是指任意一条边有方向,且不存在环路的图。
现在有一个n个点m条有向边的有向图,请你判定这是不是一个DAG图。
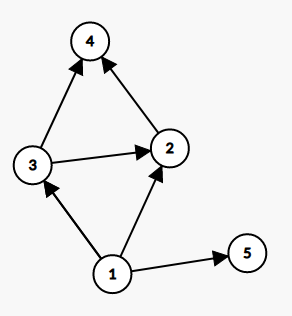
如图所示的样例中,任意一条边有方向,且不存在环路,所以该图是一个DAG图。
输入
第1行:两个正整数n,m,n表示图中点的个数,m表示图中有向边的个数。(2<=n<=100000,2<=m<=300000)
第2~m+1行:每行两个正整数u,v,表示有一条u到v的有向边。(1<=u,v<=n)输出
如果该图是DAG图,输出"Yes",否则输出"No"。(不带引号)
输入样例
10 20
1 2
1 3
1 5
1 7
1 3
1 5
2 10
2 5
2 10
2 10
2 4
3 4
3 7
3 10
4 9
5 6
5 8
6 9
7 9
8 9输出样例
Yes
思路:DAG 图判定裸题
源程序
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
#include<bitset>
#define EPS 1e-9
#define PI acos(-1.0)
#define INF 0x3f3f3f3f
#define LL long long
const int MOD = 1E9+7;
const int N = 500000+5;
const int dx[] = {-1,1,0,0,-1,-1,1,1};
const int dy[] = {0,0,-1,1,-1,1,-1,1};
using namespace std;
struct Edge{
int next;
int to;
}edge[N*2];
int cnt,head[N],son[N];
bool vis[N];
void add(int from,int to){
edge[++cnt].next=head[from];
edge[cnt].to=to;
head[from]=cnt;
}
bool flag;
void dfs(int x){
if(vis[x])
flag=false;
if(!flag)
return;
vis[x]=true;
for(int i=head[x];i!=-1;i=edge[i].next)
dfs(edge[i].to);
vis[x]=false;
}
int main(){
int n,m;
scanf("%d%d",&n,&m);
memset(head,-1,sizeof(head));
for(int i=0;i<m;i++){
int x,y;
scanf("%d%d",&x,&y);
add(x,y);
}
for(int i=1;i<=n;i++){
flag=true;
dfs(i);
if(!flag)
break;
}
if(flag)
printf("Yes\n");
else
printf("No\n");
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号