机器学习

1、机器学习是干什么的。我的理解：通过查看现在的状况，利用机器学习，预测未来可能出现的情况。（房价预测）/或者说通过一些算法、代码让机器实现一些简单的工作。（客服机器人）     编写算法，让机器人通过大量的数据、经验自己学习获得最优解。

显著式编程 和 非显著式编程：

告诉特点让其分类；让计算机自己总结规律得编程方法为非显著式编程（通过数据经验自动学习来完成任务）。

2、机器学习的分类：

监督学习：经验E是人工采集并输入计算机中的。

     分为传统监督学习（每个训练数据都有对应的标签）、非监督学习（所有训练数据都没有对应的标签）、半监督学习三种。

     另一个角度分类（基于标签的固有属性）：分类（标签是离散的值）和回归（标签是连续的值）（训练样本是时间、标签是房价，房价是连续的）  房价看成10000、100001、100002。这样就是离散的。房价化成一个曲线，就是连续的。

     监督学习算法：支持向量机、深度神经网络、人工神经网络。

     无监督学习算法：聚类、EM算法、主成分分析。

强化学习：经验E是由计算机与环境的互动获得的。计算机产生行为并获得这个行为的结果。我们只需设计收益函数。同时设计算法，让计算机自己改变自己的行为模式，去最大化收益函数。

3、机器学习的流程：

①把一个问题变成机器学习的问题    ②收集数据、处理数据、提取特征（通过训练样本取得对机器学习任务有帮助的多维数据）  ③训练模型，通过这些数据，设计模型，使得我的模型能预测未来的数据 ④关注模型的性能，通过模型获得新数据，再用新的数据进行模型的调整。    迭代这一过程。

选择什么样的问题 变成机器学习的问题呢？  -----  利益。

数据的选择？ ---- 高质量的、清洗过的数据。

模型的设计和上线？----- 设计模型需要大量的机器来跑数据。 设计了模型还不一定能用，可能部署上线很贵。

1、对数据进行特征提取、特征选择。2、使用不同的算法对特征空间做不同的划分获得不同的结果 3、研究不同场景下采用哪种算法。

 

4、支持向量机

①线性可分（把两类图形分开）：即通过直线/平面/超平面把×和⭕分开。

 

 

 

 

1、以二维下直线划分两类样本为例。我们首先可以找到很多直线使得划分两类样本。我们把直线进行平移，到相交到样本集止，交到的样本叫做支持向量。我们要找的直线就是使得

交的两平行线之间间隔最大的，并且位于中间位置的那条直线。  而用数学方法表示的话就是 

注意有 n个限制条件。就是说对于每个样本满足，如果标签yi=+1，那么样本的x要满足w转置*x+b>=1；如果标签yi=-1，那么样本的x要满足 w转置*x+b<=-1。

只有满足限制条件才能保证是线性可分的。而最小化目标函数就是找到那个超平面。

 

首先知道两个结论：

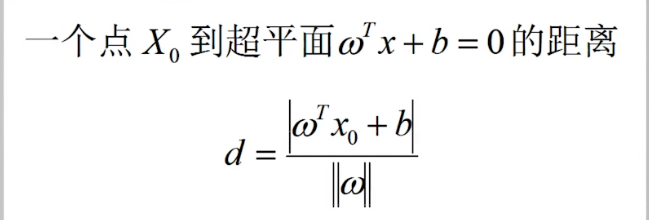  上面是绝对值、下面是w的模。

理解二位情况下的特例。  

 

之后我们要用a 对 w、b进行缩放，目的是使缩放后的平面（与原来的超平面还是一个超平面）满足     在支持向量x上 |w的转置*x+b|=1  而在非支持向量上  |w的转置*x+b|>1。

这样 支持向量到直线的距离就变成了。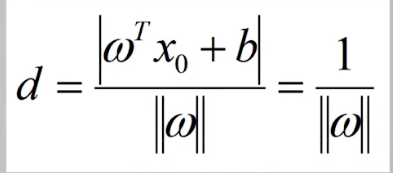

由此 我们如果要最大化支持向量到超平面的距离，就等价于最小化w的模，在这里我们转换为求最小的 1/2 w模的平方（有利于求导）。   

我们想找的是使得点到要找的平面的距离最大，而通过对平面进行改造，距离就是d最大  也就是w的模最小。 

 

这是一个凸优化中的二次规划问题：

二次规划：目标函数时二次项（1/2w模的平方）、限制条件是一次项。这样的二次规划问题，要么无解、要么只有唯一的最小值解

 

 

当线性不可分时，就需要适当放松限制条件。

 

 

或者把低维数据集的映射为高维的数据集  ， 来把二维下的线性不可分变为高维下的线性可分。