时间复杂度

代码随想录学习笔记：
时间复杂度是一个函数，它定性描述该算法的运行时间。

面试中算法的时间复杂度指的都是一般情况（即大多数情况下）。但样例不同会影响时间复杂度。

大O：用来表示上界的，通常用它描述算法的最坏情况运行时间的上界。
但快排的时间复杂度却是O(nlogn)。这里说的O代表的就是一般情况，而不是严格的上界。
不是时间复杂越低的越好（因为简化后的时间复杂度忽略了常数项等等），要考虑数据规模，如果数据规模很小甚至可以用O(n^2)的算法比O(n)的更合适（在有常数项的时候）。

log以i为底n的对数 = log以i为底j * log以j为底n的对数，所以对于O来说，忽略了底数，直接说是logn。

n个长度不超过m的字符串找出两个相同的字符串的时间复杂度：
先把字符串集合排序再遍历一遍找到两个相同字符串的方法要比直接暴力枚举的方式更快。
用快排对n个字符串的排序复杂度如何分析？
对数和字符串的快排，这两者的时间复杂度不同应该仅在比较两个目标谁大谁小的时候。
数比大小的过程时间复杂度为O(1)，而字符串要对比m个字符，所以花费O(m)的时间复杂度。
因此用快排对字符串排序复杂度为O（nlogn*m）。

递归的时间复杂度：
递归的时间复杂度 = 递归的次数（调用递归函数次数） * 每次递归的时间复杂度。（无循环就是O(1) ） 

计算x的n次方：

int function3(int x, int n) {
    if (n == 0) return 1;
    if (n == 1) return x;

    if (n % 2 == 1) {
        return function3(x, n / 2) * function3(x, n / 2)*x;
    }
    return function3(x, n / 2) * function3(x, n / 2);
}

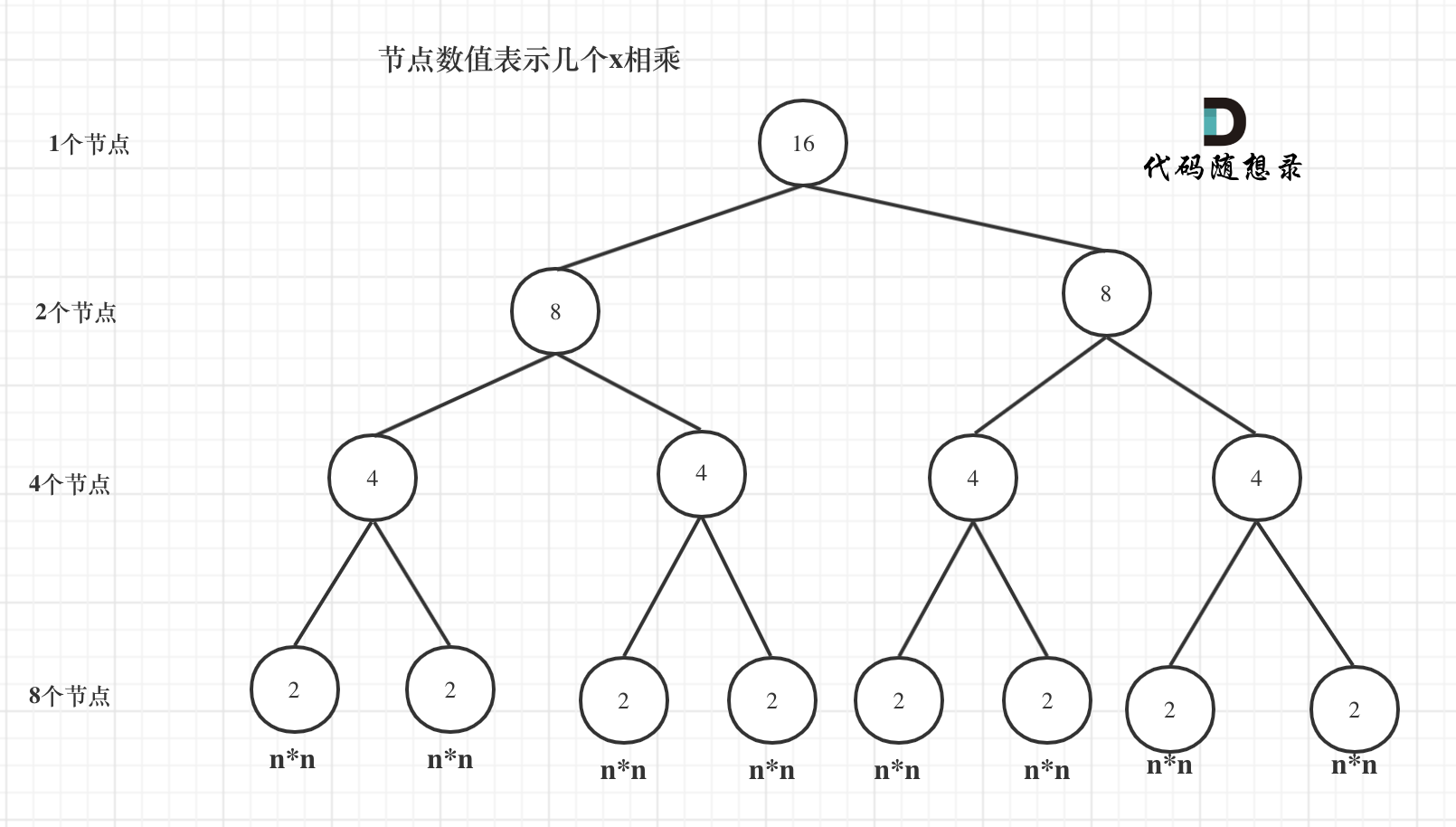
以n为16举例。上图可知，递归的次数一共就是上图结点个数——求16次方时，分别计算两个8次方。计算8次方时，分别计算两个4次方...

程序一共调用递归函数为15次。注意最后一次调用递归函数是计算2次方时，因为当1次方时是直接返回的，没有调用函数，不在递归次数内。

由递归的时间复杂度的计算可知，该算法的递归次数是n-1次，而每次递归的时间复杂度是O（1），所以O（n）。

 

优化：同样是递归，如果中途保存结果，那么会减少递归的次数。 

 

int function4(int x, int n) {
    if (n == 0) return 1;
    if (n == 1) return x;
    int t = function4(x, n / 2);// 这里相对于function3，是把这个递归操作抽取出来
    if (n % 2 == 1) {
        return t * t * x;
    }
    return t * t;
}

 

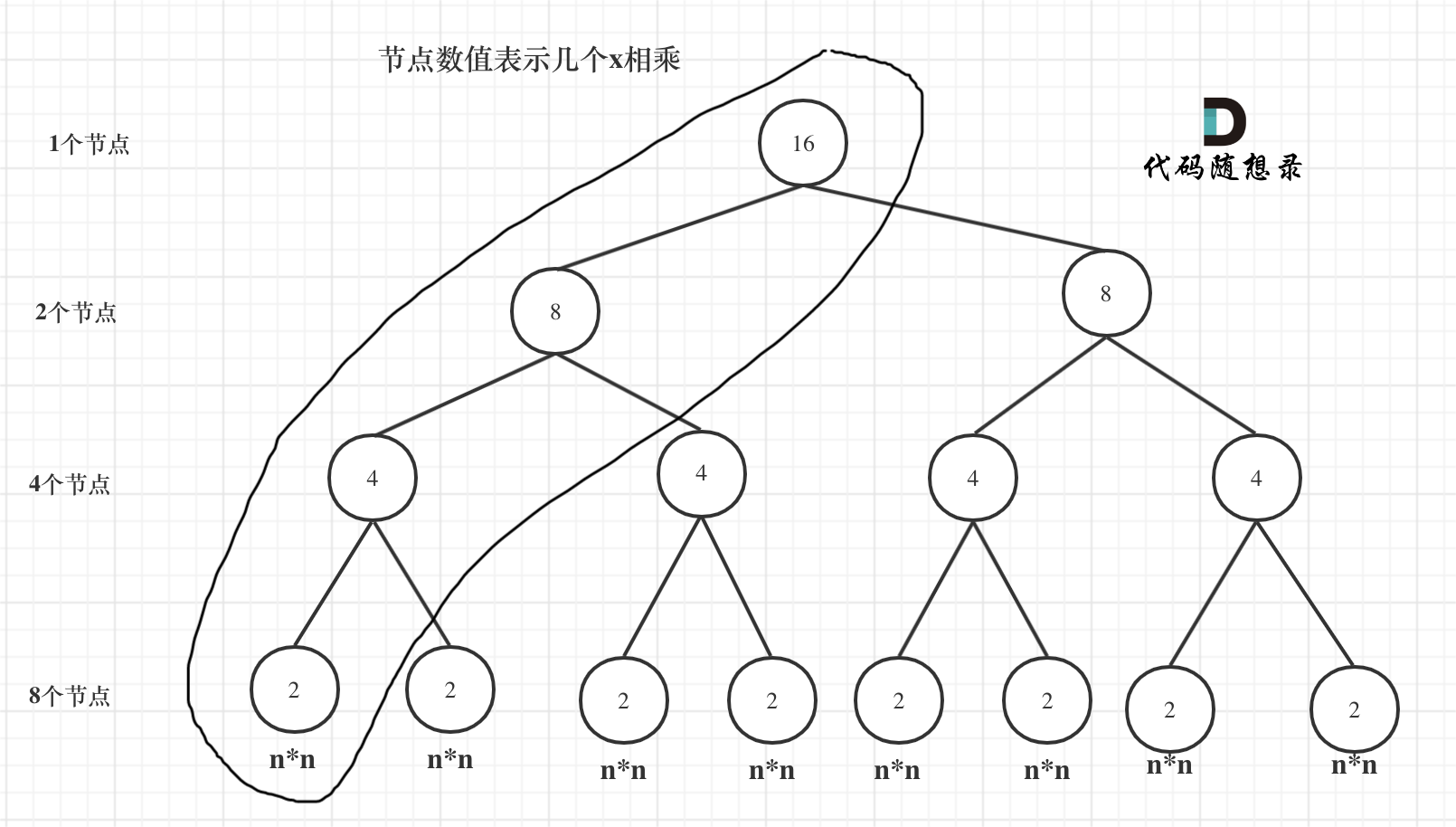
 该算法算16次时，先计算出8次方，然后在两个8次方相乘，8次方时也是如此，实际只需要左边圈出来的那些递归次数。

所以递归规程中保留计算结果会使得时间复杂度变低，这个时间复杂度为O（logn）。

 

斐波那契数列的时间复杂度：

 

int f(int n)
{
    if(n==0||n==1)
        return 1;
    if(ans[n-1]==0)
        ans[n-1]=f(n-1);
    if(ans[n-2]==0)
        ans[n-2]=f(n-2);
    ans[n]=ans[n-1]+ans[n-2];
    return ans[n];
}

我们在计算的时候先看有没有计算过，如果计算过就直接拿过来用，如果没有就调用递归求值，这样会减少递归调用的次数。可以举例看一下。

递归的时候，在计算f(n)时就已经把需要求的值求完了，而且只求了一遍。所以递归次数为O（n），每次的复杂度为O(1)，总时间复杂度为O（n）。

而如果我们直接用f(n)=f(n-1)+f(n-2) 这样计算，大概需要的时间复杂度为O(2的n次方-1)（PS:其实是小于2的n次方-1的，但用这个来估计。有点点疑问）