非线性最小二乘估计发射器位置

问题描述点击这里 问题描述点击这里

单个接收器数据对应的误差是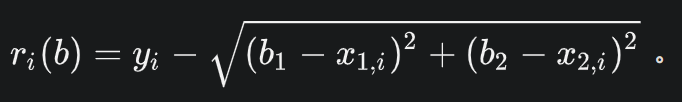

要优化的目标函数【求待定参数下的函数最小值】为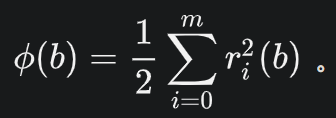
其中参数‘b’为待估计参数向量。‘m’为样本容量。

由问题实际意义可知目标函数一定存在最小值，而且对参数‘b’偏导数连续。因为‘b’是开区域，所以目标函数的最小值一定是其某个极小值。

多元函数的取极值的必要不充分条件是一阶偏导数全为零【即梯度为零向量】。

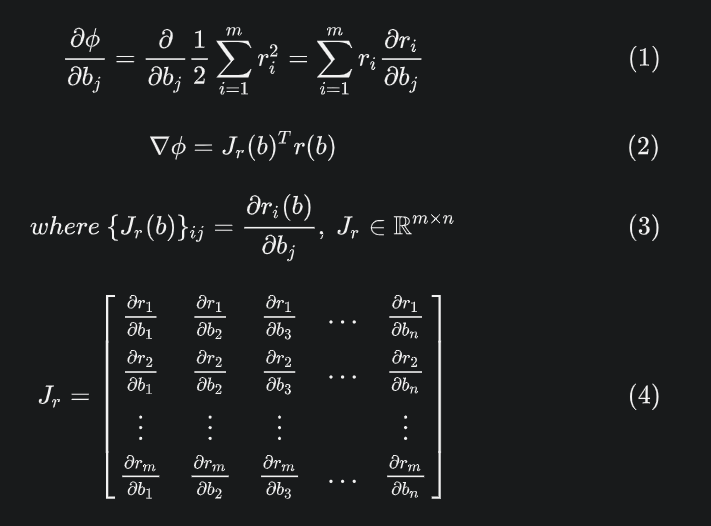
其中n是待优化参数的维度， 是r对b的雅可比矩阵。

首先让目标函数梯度为零向量：
其中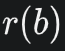是各个接收器数据对应的误差组成的列向量。

此处因为r(b)的非线性，无法通过像线性最小二乘那样解线性方程组来求参数。只能迭代求解这个优化问题。

具体如何优化求解在问题描述这篇文章里讲解的牛顿法以及高斯牛顿法非常详细。

高斯牛顿法的变种——Levenberg–Marquardt法加入了阻尼因子λ，此参数是允许在高斯牛顿或梯度下降更新之间进行更改的参数。当λ小时，该方法采用高斯-牛顿步长；当λ大时，该方法遵循梯度下降法。通常，λ的第一个值较大，因此第一步位于梯度下降方向。其背后的逻辑是，高斯-牛顿法在最终迭代中更有效，而梯度下降法在过程开始时很有用，因为该过程仍距离理想解决方案还很远。

talking is cheap, show me the code

博客园不会粘贴代码块, 所以粘贴在csdn先. 点击我跳转到代码