用复变函数求解 Fresnel 积分

现欲求解

\[\begin{aligned} I_1=\int_0^\infty \sin(x^n) \text{d}x\\ I_2=\int_0^\infty \cos(x^n) \text{d}x \end{aligned} \]

考虑构建如下图的扇形围道 \(\Gamma\)。（目的：在实轴上的积分的实部和虚部分别产生 \(I_1,I_2\)，在另一条半径返回的时候产生可以计算的实积分）设半径为 \(R\)，角度为 \(\alpha\).

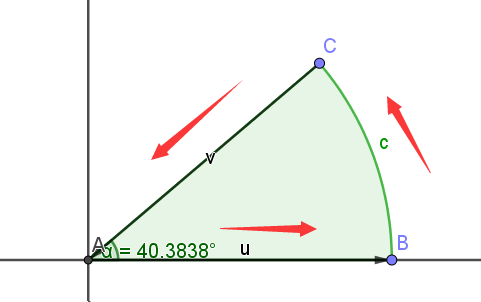
令复值函数 \(f(z)=\exp(\text{i}z^n)\). 那么根据 Cauchy-Goursat 定理

\[\oint_\Gamma f(z)\text{d}z=(\int_{AB}+\int_{BC}+\int_{CA})f(z)\text{d}z=0 \]

而

\[\int_{AB}f(z)\text{d}z=\int_0^R\exp(\text{i}x^n)\text{d}x=\int_0^R [\cos(x^n)+\text{i}\sin(x^n) ]\text{d}x \]

\[\int_{CA}f(z)\text{dz} \xlongequal{z=r\text{e}^{\text{i}\alpha}}\int_R^0 \exp(\text{i}r^n\text{e}^{n\text{i}\alpha})\text{e}^{\text{i}\alpha}\text{d}r \]

为使该路径构成实积分，需要使 \(\text{Im}(\text{i}r^2\text{e}^{n\text{i}\alpha})=0\)，因此不妨令 \(\alpha=\dfrac{\pi}{2n}\)，此时

\[\int_{CA}f(z)\text{dz}=(\cos\alpha+\text{i}\sin\alpha)\int_R^0 \exp(-r^n)\text{d}r \]

再考察弧 \(BC\)，记其为 \(L\)；则第二部分的积分为

\[\int_Lf(z)\text{d}z=\int_L \exp(\text{i}z^n)\text{d}z \]

很容易猜测该积分为 0，于是考虑应用如下引理：

I.若尔当引理 (Jordan's Lemma)

若 \(f\) 在实轴上方任意圆弧 \(L:\rho=r\text{e}^{i\theta} (0\le \theta_1\le \theta \le \theta_2 \le \pi)\) 上连续，且 \(\lim\limits_{z\to \infty} f(z)=0\)，那么对于正常数 \(\lambda\)，必有

\[\lim_{r\to+\infty} \int_Lf(z)\text{e}^{\text{i}\lambda z}\text{d}z=0 \]

II. 大圆弧引理

若 \(f\) 在任意圆弧 \(L:\rho=r\text{e}^{i\theta} (\theta_1\le \theta \le \theta_2)\) 上连续，且极限 \(\lim \limits_{z\to \infty} zf(z)=\lambda\)​ 存在且有限，那么必有

\[\lim_{r\to+\infty} \int_Lf(z)\text{d}z=\text{i}\lambda(\theta_2-\theta_1) \]

若要考虑大圆弧引理，则期待 \(z\exp(\text{i}z^n)\) 在无穷处的极限等于 0（实际上是不对的）。因此我们进行换元 \(t\gets z^n\)，则 \(t\) 也构成圆弧 \(L'\)，同时

\[\int_Lf(z)\text{d}z=\int_{L'} \dfrac{1}{n}t^{{1\over n}-1}\text{e}^{\text{i}t} \text{d}t \]

此时利用若尔当引理，可知当 \(R\to +\infty\)，第二项积分趋于 0。因此在 Cauchy-Goursat 定理给出的等式中令 \(R\to +\infty\)，立刻得：

\[\begin{aligned} &\int_0^{+\infty} [\cos(x^n)+\text{i}\sin(x^n) ]\text{d}x\\ =&(\cos\alpha+\text{i}\sin\alpha)\int_0^{\infty} \exp(-r^n)\text{d}r \end{aligned} \]

此时回顾 Gamma Function 的定义，以换元 \(t\gets r^n\) 可得

\[\int_0^{\infty} \exp(-r^n)\text{d}r=\int_0^\infty\dfrac{1}{n}t^{{1\over n}-1}\text{e}^{-t} \text{d}t=\dfrac{\Gamma(\dfrac{1}{n})}{n} \]

最终令实部和虚部分别比照，得到最终结论

\[\begin{aligned} \int_0^\infty \sin(x^n) \text{d}x&=\sin\dfrac{\pi}{2n}\dfrac{\Gamma(\dfrac{1}{n})}{n}\\ \int_0^\infty \cos(x^n) \text{d}x&=\cos\dfrac{\pi}{2n}\dfrac{\Gamma(\dfrac{1}{n})}{n} \end{aligned} \]