组合数学各类公式及应用总结
卡特兰数
应用
- 矩阵连乘: P=a1×a2×a3×……×an,依据乘法结合律,不改变其顺序,只用括号表示成对的乘积,试问有几种括号化的方案?
- 一个栈(无穷大)的进栈序列为1,2,3,…,n,有多少个不同的出栈序列?
- 在一个凸多边形中,通过若干条互不相交的对角线,把这个多边形划分成了若干个三角形。任务是键盘上输入凸多边形的边数n,求不同划分的方案数
- 给定N个节点,能构成多少种不同的二叉搜索树?
- 给定n对括号,求括号正确配对的字符串数
递推式:
前几项:
1,1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796
第一类Stirling数
应用
- 将n个物体排成k个非空循环排列(非空的)的方法数
递推式: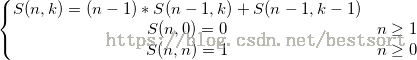
前几项:

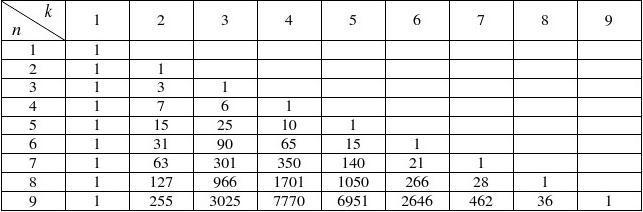
第二类Stirling数
**应用**
- n个元素划分成k个无序集合的方案数
递推式:
前几项:
贝尔数
应用
- 包含n个元素的集合的划分方法的数目。
递推式:
![这里写图片描述]() ,其中
,其中为第二类Stirling数
前几项:
1, 1, 2, 5, 15, 52, 203, 877,4140, 21147, 115975
那罗延数
应用
- 在由n对”(“和”)”组成的字符串中,共有k对”(“与”)”相邻,这样的字符串一共有N(n,k)个
递推式: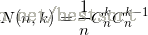
前几项:
| n\k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | |||||||
| 2 | 1 | 1 | ||||||
| 3 | 1 | 3 | 1 | |||||
| 4 | 1 | 6 | 6 | 1 | ||||
| 5 | 1 | 10 | 20 | 10 | 1 | |||
| 6 | 1 | 15 | 50 | 50 | 15 | 1 | ||
| 7 | 1 | 21 | 105 | 175 | 105 | 21 | 1 | |
| 8 | 1 | 28 | 196 | 490 | 490 | 196 | 28 | 1 |
默慈金数
应用
- 在一个圆上的n个点间,画出彼此不相交的弦的全部方法的总数
递推式:
前几项:
1, 2, 4, 9, 21, 51, 127, 323, 835, 2188, 5798, 15511, 41835, 113634
卢卡斯定理
应用:
- 大组合数求模
公式:



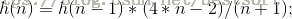
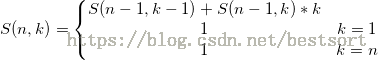
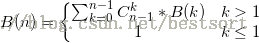
 ,其中
,其中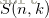 为第二类Stirling数
为第二类Stirling数 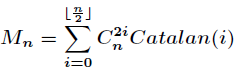
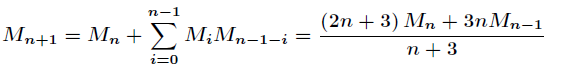

 浙公网安备 33010602011771号
浙公网安备 33010602011771号