DS博客作业03--树
0.PTA得分截图(215)
1.本周学习总结
1.1 总结树及串内容
串的BF算法
匹配方法:遍历整个串直到找到子串
缺点:效率低,主串需要回溯到上一个遍历点的下一个字符,子串每次都从头开始
优点:是比较容易理解的一种算法
匹配图解:


串的KMP算法
匹配方法:
改进:主串无需回溯,子串不一定需要从头开始遍历
二叉树存储结构、建法、遍历及应用
一般存储结构
typedef struct BiTNode
{
char data;
struct BiTNode* lchild, * rchild;
}BTNode, * BTree;
先序建树
BTree CreateTree(char str[], int &i)
{
BTree T;
int len;
len = Strlen(str);
T = new BTNode;
if (i > len)
{
return NULL;
}
if (str[i] == '#')
{
return NULL;
}
T->data = str[i];
T->lchild = CreateTree(str, ++i);
T->rchild = CreateTree(str, ++i);
return T;
}
层次建树
BTree CreateTree(char str[], int& i)
{
BTree T;
int len;
len = Strlen(str);
T = new BTNode;
if (i > len)
{
return NULL;
}
if (str[i] == '#')
{
return NULL;
}
T->data = str[i];
T->lchild = CreateTree(str, ++i);
T->rchild = CreateTree(str, ++i);
return T;
}
先序中序后序遍历
void Print(BinTree BT)
{
if (BT != NULL)
{
printf(" %c", BT->Data);//放在这是先序
PreorderPrintLeaves(BT->Left);
printf(" %c", BT->Data);//放这是中序
PreorderPrintLeaves(BT->Right);
printf(" %c", BT->Data);//放这是后序
}
}
//区别在于先访问子树还是先录入数据
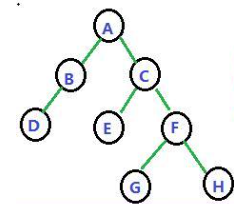
- 先序:ABDCEFGH
- 中序:DBAECGFH
- 后序:DBEGHFCA
层次遍历
void LevelOrderPrintNodes(BTree LT)
{
if (LT == NULL)
{
cout << "NULL";
return;
}
queue<BTree>BT;
BTree T;
int flag = 1;
BT.push(LT);
while (!BT.empty())
{
T = BT.front();
BT.pop();
if (flag == 1 && T != NULL)
{
cout << T->data;
flag = 0;
}
else if (flag == 0 && T != NULL)
{
cout << " " << T->data;
}
if (T->lchild != NULL)
{
BT.push(T->lchild);
}
if (T->rchild != NULL)
{
BT.push(T->rchild);
}
}
}
应用:如求二叉树高度(递归法)
int GetHeight(BinTree BT)
{
if (BT == NULL)return 0;
if (BT->Left == NULL && BT->Right == NULL)return 1;
if (GetHeight(BT->Left) > GetHeight(BT->Right))
{
return GetHeight(BT->Left) + 1;
}
else
{
return GetHeight(BT->Right) + 1;
}
}
树的结构、操作、遍历及应用
双亲结构
typedef struct
{
int data;
int parent;
} PTree[MaxSize];
孩子结构
typedef struct node
{
int data;
struct node *sons[MaxSons];
//兄弟链就是在这加上一条指向同层的指针
} TNode;
- 遍历操作与二叉树类似
线索二叉树
typedef struct BiTNode
{
int data;
int ltag;
int rtag;
struct BiTNode* lchild, *rchild;
}BTNode,*BTree;
线索二叉树利用二叉树空域存放指针指向其它结点
- 除第一个结点外每个结点有且仅有一个直接前驱结点;除最后一个结点外每一个结点有且仅有一个直接后继结点
- 根据线索不同分中序和后序线索二叉树
哈夫曼树、并查集
typedef struct
{
int weight;//权重
int parent, left, right;
}HTNode, *HuffmanTree;
- wpl=叶节点*链路长度
如:
![]()
- wpl=(7+8+9)*3=72
- 哈夫曼树是一种带权路径长度最短的二叉树,极大提高了代码的效率,是最优二叉树
哈夫曼编码
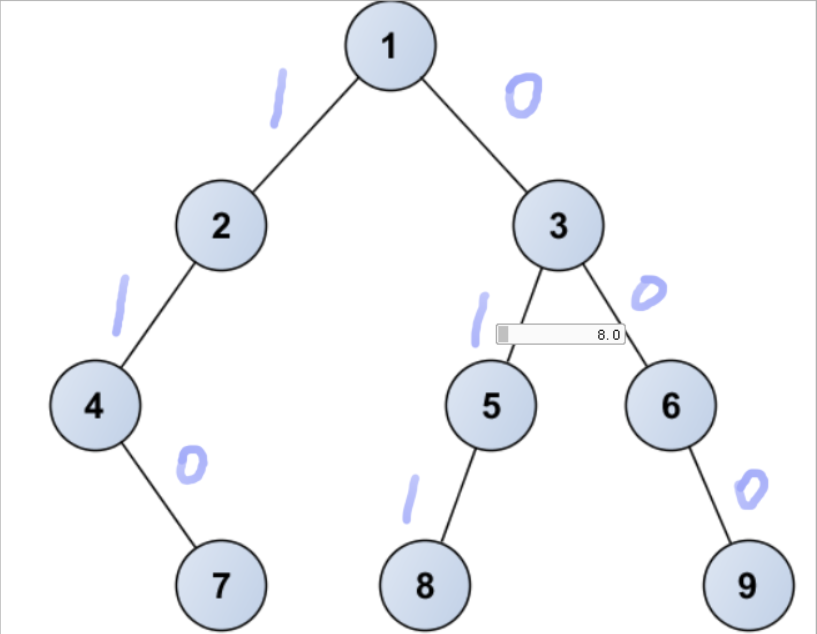
- 从根节点开始,将左孩子编码1,右孩子编码0,直到各节点为止的编码连起来就是哈夫曼编码
- 如上图所示
9的编码为000,7的编码为110等
1.2.谈谈你对树的认识及学习体会。
树的知识掌握的不好,用起来不熟练,有些地方解析得不够透彻,就听不懂。
2.阅读代码
2.1 左叶子之和
- 题目
![]()
- 解题代码
![]()
2.1.1 该题的设计思路

- 该题不直接访问叶子结点,而是在叶子结点的上一个结点来访问左结点,巧妙避开了访问右结点的情况
- 空间复杂度和时间复杂度都为O(n)
2.1.2 该题的伪代码
//递归法
int sumOfLeftLeaves(struct TreeNode* root)
sum=0
if树为空,返回0
if左子树不空
if树的左子树为叶节点
sum=叶节点的值
else
sum=sumOfLeftLeaves(左子树)//得到左子树的左叶子的值
sum+=sumOfLeftLeaves(右子树)//得到右子树左叶子的值并加上左子树的左叶子的值
返回sum的值
2.1.3 运行结果

2.1.4分析该题目解题优势及难点
- 该解法利用了递归,缩短了代码长度,仅使用简单的语法,阅读难度较低
- 题目难点在于如何避开右叶子仅仅得到左叶子的值
2.2 打劫家舍III


2.2.1设计思路
- 思路:每次递归时算出该结点使用与不使用的值并返回最大值,关键在于动态比较
- 时间和空间复杂度都为O(n)
2.2.2伪代码
int getMaxSum(struct TreeNode *root, int *sumRoot, int *sumNoRoot)
if树为空,返回0
计算不取当前结点的最大值(存入sumNoRoot)
计算取当前结点的最大值(sumRoot)
二者比较返回较大者
int rob(struct TreeNode* root)
定义sumRoot,sumNoRoot
调用getMaxSum函数
2.2.3运行结果

2.2.4分析该题目解题优势及难点
- 题目需要利用动态规划,在递归时要根据结果判断是否是最大值
- 题目难点在于如何保证所求的值不是俩个直接相连的结点
2.3路径总和III

2.3.1设计思路
- 思路:双递归法,类先序遍历,找到符合要求的值并返回个数
![]()
- 时间和空间复杂度都为O(n)
2.3.2伪代码
int helper(TreeNode* root, int sum)//sum的值为要求的值
if树为空,返回0
sum-当前结点值
返回(如果sum为0证明减去的结点值刚好=sum,返回1,否则0)+helper(左子树,sum)+helper(右子树,sum)
int pathSum(TreeNode* root, int sum)
if树为空,返回0
返回调用函数helper后的结果
2.3.3运行结果

2.3.4分析该题目解题优势及难点
- 本题极大利用递归解决,大幅缩短代码
- 难点:找到链路中和为某个值的链路
2.4另一个树的子树

2.4.1设计思路
- 思路:对每一棵子树进行比较
- 时间和空间复杂度O(n)
2.4.2伪代码
bool compare (struct TreeNode* p1,struct TreeNode* p2)
if p1,p2都为空,返回true
if p1,p2若一方为空一方不空,返回false//因为上一句已经比较过都为空的情况,不会出现都为空返回false
if p1的数据不等于p2数据,返回false
返回p1p2左右子树比较地结果,同时匹配才返回正确
bool isSubtree(struct TreeNode* s, struct TreeNode* t)
if s为空,返回false
对所有子树调用compare函数比较,只要有任意一颗子树和目标子树匹配就返回正确
2.4.3运行结果
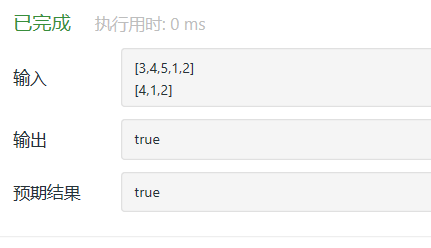
2.4.4分析该题目解题优势及难点
- 解法利用递归节省大量代码,而不是一个结点一个结点地去比较,是一种较好的方法
- 难点:以什么样的方法比较子树与目标树






 浙公网安备 33010602011771号
浙公网安备 33010602011771号