33dai OJ 好题总结

33dai oj 好题总结

• 智
• • 10pts
  • 60pts
  • 100pts
• 讨厌的线段树
• • 30pts
  • 100pts
• 杭州
• 北京
• 西安

智

10pts

\qquad 本题性质 $1$ 的 $10pts$ 是十分好拿的。我们只需将所有 $s_i=1$ 的飞行员的 $v_i$ 取个 $\max$，并与所有 $s_i=n$ 的飞行员的 $v_i$ 和取 $\max$ 即可。

60pts

\qquad 在上面 $10pts$ 的基础上，我们来考虑 $n\le 1000$ 的该怎么搞。注意到 $s_i\le n$，且每个人都有一个 $v_i$，看起来是不是及其像背包呢？我们只需裸着做一遍背包即可。考场上我也就只能想到这一步了

\qquad $Code:$

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int maxn = 1e5 + 5;
int n;
int v[maxn], s[maxn];

inline int read() {
	int x = 0; char ch = getchar();
	while(!isdigit(ch)) ch = getchar();
	while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
	return x;
}

namespace task1 {
	const int N = 1e3 + 10;
	LL dp[N];
	
	void sol() {//背包板子
		for(int i = 1; i <= n; i ++) {
			for(int j = s[i]; j >= 1; j --)
				dp[j] = max(dp[j], dp[j - 1] + 1LL * v[i]);
		}
		LL ans = 0;
		for(int i = 1; i <= n; i ++) ans = max(ans, dp[i]);
		printf("%lld\n", ans);
	}
}

int main() {
	n = read();
	for(int i = 1; i <= n; i ++) v[i] = read(), s[i] = read();
	if(n <= 1000) task1::sol();
	else {
		bool flag = 0;
		for(int i = 1; i <= n; i ++) if(s[i] != 1 && s[i] != n) {flag = 1; break;}
		if(!flag) {//子任务1
			LL ans = 0, sum = 0;
			for(int i = 1; i <= n; i ++) {
				if(s[i] == 1) ans = max(ans, 1LL * v[i]);
				else sum += 1LL * v[i];
			}
			ans = max(ans, sum);
			printf("%lld\n", ans);
			return 0;
		}
	}
	return 0;
}

100pts

\qquad 背包的时间复杂度，众所周知，极限也是 $O(n^2)$ 了，无法进一步优化。

\qquad 现在，我们想：如果没有人数限制，我们会怎么办呢？显然，我们会将所有飞行员按 $v_i$ 排序，然后从大到小去选。那么有人数限制了，该怎么办呢？我们考虑：若最优选择方案选择的人员集合为 $S$，那么这个 $S$ 一定满足：1、有一个 $s_i$ 最小的飞行员（废话），设这个人的编号为 $p$；2、$S$ 中剩下的飞行员一定是所有 $s_i\ge s_p$ 的飞行员中，$v_i$ 前 $s_p-1$ 大的飞行员。证明并不难，可以感性理解。有了这个结论，我们便思考：若将 $s_i$ 从大到小排序，然后依次枚举每个飞行员，查找前面已枚举的飞行员中 $v_i$ 排前 $s_i-1$ 大的飞行员的 $v_i$ 和，然后取 $\max$，便是最终答案。根据上面的结论，我们可以轻易的证明这个做法一定包含了最优情况。这个做法的实现方法有很多，例如 $set$，堆，线段树均可。

\qquad $Code:$

#include <bits/stdc++.h>//感觉还是线段树好写一点（？）
using namespace std;

typedef long long LL;
const int maxn = 1e5 + 5;
int n, tot;
struct node {
	int vi, si;
}a[maxn];
struct Segment {//值域线段树
	int ls, rs, num;
	LL sum;
	#define ls(x) tree[x].ls
	#define rs(x) tree[x].rs
	#define num(x) tree[x].num
	#define sum(x) tree[x].sum
}tree[maxn * 32 * 2];

inline int read() {
	int x = 0; char ch = getchar();
	while(!isdigit(ch)) ch = getchar();
	while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
	return x;
}

bool cmp(node a, node b) {
	return (a.si > b.si || (a.si == b.si && a.vi > b.vi));
}

inline int build() {
	tot ++;
	ls(tot) = rs(tot) = num(tot) = sum(tot) = 0;
	return tot;
}

LL query(int p, int l, int r, int s) {
	if(num(p) <= s) return sum(p);
	int mid = l + r >> 1; LL cnt = 0;
	cnt += query(rs(p), mid + 1, r, s);
	if(num(rs(p)) < s) cnt += query(ls(p), l, mid, s - num(rs(p)));
	return cnt;
}

inline void update(int p) {
	num(p) = num(ls(p)) + num(rs(p));
	sum(p) = sum(ls(p)) + sum(rs(p));
}

void change(int p, int l, int r, int v) {
	if(l == r) {
		num(p) ++, sum(p) += 1LL * v;
		return ;
	}
	int mid = l + r >> 1;
	if(v <= mid) {
		if(!ls(p)) ls(p) = build();
		change(ls(p), l, mid, v);
	}
	else {
		if(!rs(p)) rs(p) = build();
		change(rs(p), mid + 1, r, v);
	}
	update(p);
}

int main() {
	n = read();
	for(int i = 1; i <= n; i ++) a[i].vi = read(), a[i].si = read();
	sort(a + 1, a + n + 1, cmp);
	LL ans = 0;
	int root = build();
	for(int i = 1; i <= n; i ++) {
		ans = max(ans, 1LL * a[i].vi + query(1, 1, 1e9, a[i].si - 1));
		change(1, 1, 1e9, a[i].vi);
	}
	printf("%lld\n", ans);
	return 0;
}

讨厌的线段树

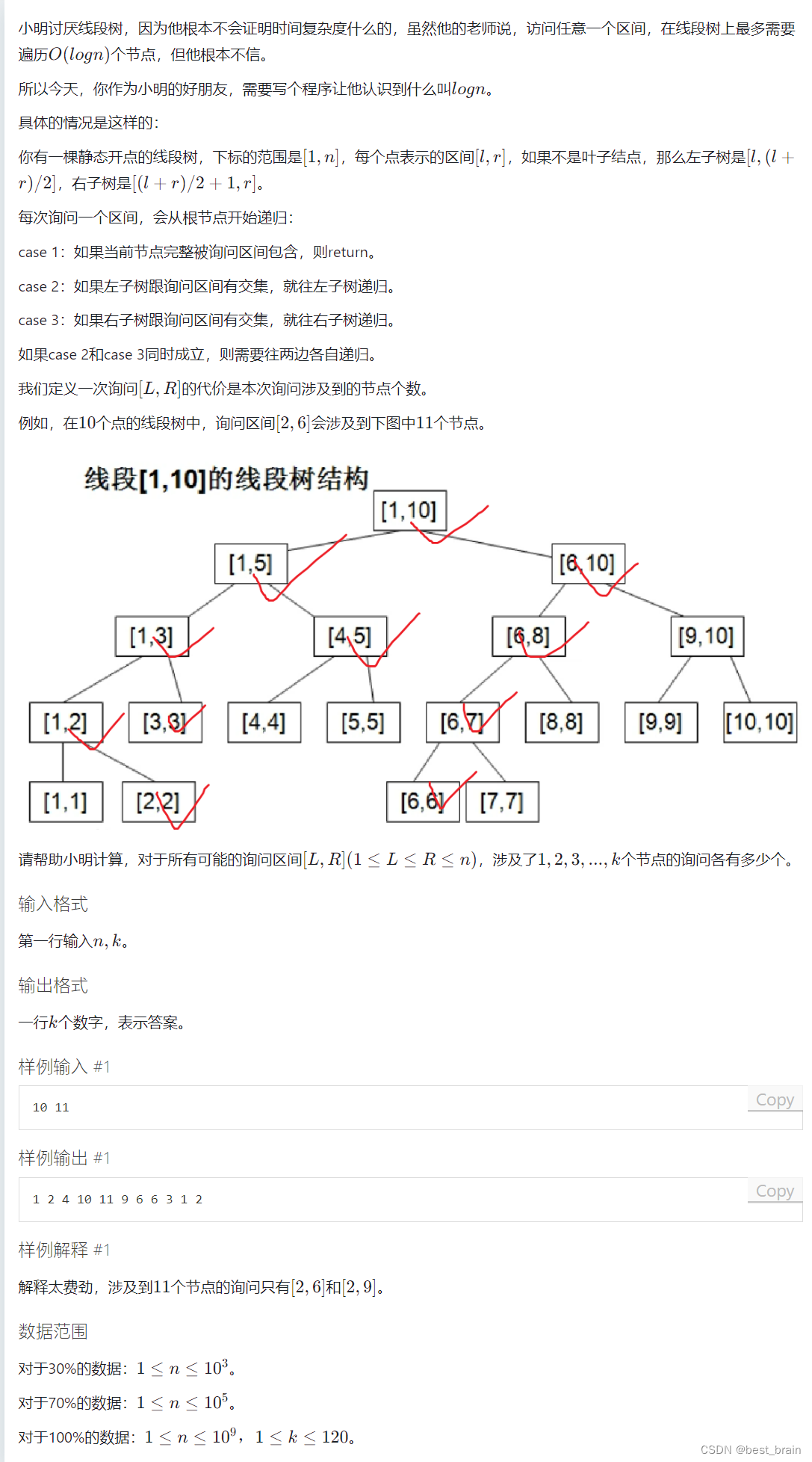
30pts

\qquad 本题的 $30pts$ 是非常好拿的，直接 $O(n^{2}lo{g}_{2}n)$ 将所有区间在线段树上模拟一下即可。

\qquad $Code:$

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int maxk = 150;
int n, k;

inline int read() {
	int x = 0; char ch = getchar();
	while(!isdigit(ch)) ch = getchar();
	while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
	return x;
}

namespace task1 {
	LL ans[maxk];
	int num = 0;
	
	void query(int p, int l, int r, int tl, int tr) {
		num ++;
		if(tl <= l && r <= tr) return ;
		int mid = l + r >> 1;
		if(tl <= mid) query(p << 1, l, mid, tl, tr);
		if(tr > mid) query(p << 1 | 1, mid + 1, r, tl, tr);
	}
	
	void sol() {
		for(int i = 1; i <= n; i ++)
			for(int j = i; j <= n; j ++) {
				num = 0;
				query(1, 1, n, i, j);
				ans[num] ++;
			}
		for(int i = 1; i <= k; i ++) printf("%lld ", ans[i]);
	}
}

int main() {
	n = read(), k = read();
	task1::sol();
	return 0;
}

100pts

\qquad 本题的正解可谓十分之妙。我们想，线段树上的节点都满足一个性质：若两个节点长度相同，那么以这两个节点为根的子树结构一定完全相同。这让我们意识到，从长度入手说不定是个很好的选择，所以我们以长度划分阶段，设计 $dp$ 状态：设 $d{p}_i{,}_j{,}_{0/1}{,}_{0/1}$ 表示长度为 $i$，该区间内包含 $j$ 个被询问节点，查询区间与当前区间的左右端点是否贴合。实现用记忆化搜索，在转移时正常分类讨论即可。

\qquad $Code:$

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
int n, k;
map < int , LL > dp[130][2][2];//map<i,ans>dp[j][k][l]:长度为i的区间，占有j个节点，是否贴合左右端点，方案数为ans
//长度那一维太大了，用map来存
LL Get(int n, int c, int l, int r) {
	if(c <= 0) return 0;
	if(dp[c][l][r].find(n) != dp[c][l][r].end()) return dp[c][l][r][n];
	if(l && r) return dp[c][l][r][n] = (c == 1);
	if(n == 1) return dp[c][l][r][n] = 0;
	LL &p = dp[c][l][r][n];
	if(!l && r) {
		//l:0,0 r:0,1/1,1
		p += Get(n / 2, c - 1, 0, 1) + Get(n / 2, c - 1, 1, 1);
		//l:0,1 r:1,1
		p += Get((n + 1) / 2/*细节：若n为奇数，那么左子树长度为(n+1)/2*/, c - 2, 0, 1) * Get(n / 2, 1, 1, 1);
	}
	if(l && !r) {
		//l:1,0/1,1 r:0,0
		p += Get((n + 1) / 2, c - 1, 1, 0) + Get((n + 1) / 2, c - 1, 1, 1);
		//l:1,1 r:1,0
		p += Get((n + 1) / 2, 1, 1, 1) * Get(n / 2, c - 2, 1, 0);
	}
	if(!l && !r) {
		//l:0,0/0,1 r:0,0
		p += Get((n + 1) / 2, c - 1, 0, 0) + Get((n + 1) / 2, c - 1, 0, 1);
		//l:0,0 r:1,0/0,0
		p += Get(n / 2, c - 1, 1, 0) + Get(n / 2, c - 1, 0, 0);
		//l:0,1 r:1,0
		for(int dat = 1; dat < c; dat ++)
			p += Get((n + 1) / 2, dat, 0, 1) * Get(n / 2, c - 1 - dat, 1, 0);
	}
	return p;
}

LL solve(int n, int c) {
	return Get(n, c, 0, 0) + Get(n, c, 0, 1) + Get(n, c, 1, 0) + Get(n, c, 1, 1);
}

int main() {
	scanf("%d%d", &n, &k);
	for(int i = 1; i <= k; i ++) printf("%lld ", solve(n, i));
	return 0;
}

杭州

\qquad 本题的部分分十分简单，在此不细说。

\qquad 对于本题，发现同时具备删边和求距某点最远点之间的距离两个操作。显然，在进行删除操作时动态取 $\max$ 是非常难处理的。按照常见套路，不难想到正难则反。倒着处理每个操作，删边看成加边，动态记录最大值。要维护联通块，不难想到并查集。那么连通块内距离最大值怎么处理呢？下面给出两个结论：1、在一棵树上，距某个点最远的点一定是这棵树直径的两端点之一；2、两棵树通过一条边连成一棵新树，这棵新树的直径的两端点一定是原来两树直径的四个端点之间的两个。根据直径的定义、性质以及反证法，是不难证明出这两条结论的。现在，可能有人会问：一直在动态加边，我该怎么快速处理连通块内两点之间的距离呢？确实是个好问题。我们想：虽然这棵树的边不全，但是树的形态是不变的，而且在树上，两点若在同一连通块内，那么连接它们的路径上的所有点也都一定在这个连通块内，所以我们只需在原树上处理两点之间的距离即可。这道题就顺利的解决了。

\qquad $Code:$

#include <bits/stdc++.h>
using namespace std;

const int maxn = 2e5 + 10;
int n, m;
struct pic {
	int to, lst;
}edge[maxn << 1];
struct node {
	int opt, x;
}q[maxn];
struct bing {
	int dis, x, y;
}t[maxn];//记录每个联通块的直径的左右端点及长度
int head[maxn], tot = 0, bin[maxn], f[maxn][25], dep[maxn], st[maxn], ed[maxn], ans[maxn];
bool flag[maxn];

inline int read() {
	int x = 0; char ch = getchar();
	while(!isdigit(ch)) ch = getchar();
	while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
	return x;
}

inline void add(int x, int y) {
	edge[++ tot] = {y, head[x]};
	head[x] = tot;
}

void dfs(int x, int fa) {
	f[x][0] = fa, dep[x] = dep[fa] + 1;
	for(int i = 1; i <= 20; i ++) f[x][i] = f[f[x][i - 1]][i - 1];
	for(int i = head[x]; i; i = edge[i].lst) {
		int v = edge[i].to;
		if(v == fa) continue;
		dfs(v, x);
	}
}

int Find(int x) {
	int j = x, k = x, temp;
	while(k != bin[k]) k = bin[k];
	while(j != bin[j]) temp = bin[j], bin[j] = k, j = temp;
	return k;
}

int lca(int x, int y) {
	if(dep[x] < dep[y]) swap(x, y);
	for(int i = 20; i >= 0; i --) {
		if(dep[f[x][i]] >= dep[y]) x = f[x][i];
	}
	if(x == y) return x;
	for(int i = 20; i >= 0; i --) {
		if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
	}
	return f[x][0];
}

int Get(int x, int y) {//树上两点间距离：dep[x]+dep[y]-2*dep[lca(x,y)]
	return dep[x] + dep[y] - 2 * dep[lca(x, y)];
}

void merge(int x, int y) {//在合并两点同时维护新连通块直径
	int fx = Find(x), fy = Find(y);
	bin[fy] = fx;
	bing xx = t[fx], yy = t[fy];
	int x_x = Get(t[fx].x, t[fy].x), x_y = Get(t[fx].x, t[fy].y);
	int y_x = Get(t[fx].y, t[fy].x), y_y = Get(t[fx].y, t[fy].y);
	t[fx] = (xx.dis > yy.dis ? xx : yy);
	t[fx] = (t[fx].dis > x_x ? t[fx] : (bing){x_x, xx.x, yy.x});
	t[fx] = (t[fx].dis > x_y ? t[fx] : (bing){x_y, xx.x, yy.y});
	t[fx] = (t[fx].dis > y_x ? t[fx] : (bing){y_x, xx.y, yy.x});
	t[fx] = (t[fx].dis > y_y ? t[fx] : (bing){y_y, xx.y, yy.y});
}

int main() {
	n = read(), m = read();
	for(int i = 1; i < n; i ++) st[i] = read(), ed[i] = read(), add(st[i], ed[i]), add(ed[i], st[i]);
	for(int i = 1; i <= m; i ++) {
		q[i] = {read(), read()};
		if(q[i].opt == 1) flag[q[i].x] = 1;
	}
	dfs(1, 0);
	for(int i = 1; i <= n; i ++) bin[i] = i, t[i] = {0, i, i};
	for(int i = 1; i < n; i ++) {
		if(!flag[i]) merge(st[i], ed[i]);//这条边一直存在
	}
	for(int i = m; i >= 1; i --) {
		if(q[i].opt == 1) merge(st[q[i].x], ed[q[i].x]);
		else {
			int fx = Find(q[i].x);
			ans[i] = max(Get(q[i].x, t[fx].x), Get(q[i].x, t[fx].y));
		}
	}
	for(int i = 1; i <= m; i ++) (q[i].opt == 2 ? printf("%d\n", ans[i]) : q[i].opt = 1);
	return 0;
}

北京

\qquad 考场上随机化怒艹 0pts

\qquad 首先，看到位运算，我们就应想到：按位考虑计算。接着，注意到：这是与运算，与运算有什么性质呢？不难发现，若让 $a\&=b$，$b$ 中哪些数位（二进制下）会对 $a$ 产生影响呢？显然是低于 $a$ 最高数位的那些位。也就是：一个数 $x$ 只会被数位低于 $Highes{t}_x$ 的数改变，数位高于 $Highes{t}_x$ 的数是不会对 $x$ 产生影响的。所以我们可以按位进行贪心：假设我们当前考虑到第 $i$ 位，在所有数中最高位为 $i$ 的数有 $num$ 个。那么这 $num$ 个数在本次操作后就再也不会被修改。我们将这 $num$ 个数的 $s_i$ 相加，若与最初所有数的 $s_i$ 和符号相同，此时改变才有意义，否则只会让改完后的和离符号相反越来越远。此时，我们让所有第 i 位为 1 的数的 $s_i$ 全部取反，并让答案加上 $1<<i$ 即可。

\qquad $Code:$

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int maxn = 3e5 + 10;
int n;
LL val[maxn], mask[maxn], h[maxn];

int main() {
	scanf("%d", &n);
	LL sum = 0;
	for(int i = 1; i <= n; i ++) {
		scanf("%lld%lld", &val[i], &mask[i]), sum += val[i];
		LL M = mask[i];
		while(M) M >>= 1LL, h[i] ++;//预处理数位
	}
	if(sum < 0) {//保证最初的和为正数，方便后面判断
		for(int i = 1; i <= n; i ++) val[i] = -val[i];
	}
	LL s = 0;
	for(int i = 0; i <= 62; i ++) {
		LL num = 0;
		for(int j = 1; j <= n; j ++) {
			if(h[j] - 1 == i) num += val[j];//加上所有最高位为i的数的s[i]
		}
		if(num > 0) {//填1有意义
		//这里还有一个小细节：当num=0时，必须填0，不能填1
		//理论上讲，num=0时，填1填0不影响，但是过不掉这道题
		//为什么不能填1？因为有一个反例在数据中（雾）
		//为什么填0一定对？
		/*
		根据题目中所有数的val和不为0可知，一定存在一个数位p，使得最高位为p的数的val和不为0；
		在这个位置我们便可以完成填1的操作来调控正负，让答案合法，所以填0一定正确
		*/
			for(int j = 1; j <= n; j ++) {
				if((mask[j] >> i) & 1) val[j] = -val[j];
			}
			s |= (1LL << i);
		}
	}
	printf("%lld\n", s);
	return 0;
}

西安

\qquad 首先，本题的 $60pts$ 是非常好拿的。我们只需找两个前缀和模 $a$ 的值相同的点，答案就是这两个点包成的左开右闭区间。

\qquad 对于正解，我们首先考虑一个数字 $x$, 若 $f(x)=y$，那么 $f(x+10^{18})=y+1$。所以我们设 $p\equiv {\sum }_{i=0}^{10^{18-1}}f(i)\mathrm{mod}a$，则

${\sum }_{i=1}^{10^{18}}f(i)\equiv 1+{\sum }_0^{10^{18}-1}=1+p\mathrm{mod}a$
${\sum }_{i=2}^{10^{18}+1}f(i)\equiv 2+{\sum }_0^{10^{18}-1}=2+p\mathrm{mod}a$
$\dots$
${\sum }_{i=a-p}^{10^{18}+a-p-1}f(i)\equiv a-p+{\sum }_0^{10^{18}-1}=a-p+p=a\mathrm{mod}a$
即${\sum }_{i=a-p}^{10^{18}+a-p-1}f(i)\equiv 0\mathrm{mod}a$

\qquad 所以我们令 $l=a-p,r=10^{18}+a-p+1$，此时的 $l,r$ 就是答案。现在，我们考虑 $p$ 怎么求。${\sum }_0^{10^{18}-1}f(i)$ 可以转化为：一共有 $18$ 个格子，每个格子可以放 $0\sim 9$，求所有方案放入的数字和。我们可以枚举 $0\sim 9$ 的每个数字，再枚举它填 $1\sim 18$ 个格子，然后运算求和。

$p={\sum }_{i=0}^{9}i\times {\sum }_{j=0}^{18}{C}_{18}^j\times 9^{18-j}$

\qquad 经过一顿化简，可以求出 $p=81\times 10^{18}$。

\qquad 最终，本题也是在极短的代码中解决了。

$Code:$

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
LL a, INF = 1e18;

inline LL read() {
	LL x = 0; char ch = getchar();
	while(!isdigit(ch)) ch = getchar();
	while(isdigit(ch)) x = (x << 1LL) + (x << 3LL) + (ch ^ 48), ch = getchar();
	return x;
}

int main() {
	a = read();
	LL l = (a - (((INF % a) * 9LL) % a * 9LL) % a);
	LL r = l + INF - 1;
	printf("%lld %lld\n", l, r);
	return 0;
}