leetcode刷题
二叉树.
226. 翻转二叉树
Q: 沿中轴线对称翻转一颗二叉树.
这种题还是尽量递归解决吧
TreeNode* invertTree(TreeNode* root) {
if(!root) return root;
invertTree(root->left); invertTree(root->right);
swap(root->left, root->right);
return root;
}
101. 对称二叉树
Q: 判断一颗二叉树是否是对称的.
bool isSymmetric(TreeNode* root) {
if (!root) return true;
return dp(root->left,root->right);
}
bool dp(TreeNode* left, TreeNode* right){
if(left==NULL && right ==NULL) return true;
if(left==NULL || right ==NULL) return false;
if(left->val!=right->val)return false;
return dp(left->left,right->right) && dp(left->right,right->left);
}
104. 二叉树的最大深度
Q: 返回二叉树的最大深度 (int).
递归一句话.
int maxDepth(TreeNode* root) {
if(root==NULL) return 0;
return max(maxDepth(root->left),maxDepth(root->right)) + 1;
}
111. 二叉树的最小深度
Q: 返回给定二叉树的最小深度.
难点, 涉及到如果是NULL但是不是叶子的话, 就不是最小深度. 特化返回叶子的深度.
//这个递归挺难得...
int minDepth(TreeNode* root) {
if(!root) return 0;
if(!root->left && root->right)
return 1 + minDepth(root->right);
if(!root->right && root->left)
return 1 + minDepth(root->left);
return 1 + min(minDepth(root->left), minDepth(root->right));
}
257. 二叉树的所有路径
Q: 返回所有叶子到根节点的路径. vector<string>
这个递归感觉有点浪费空间哎....
跟前面一样 判断叶子节点 !left && !right
vector<string> res;
void dfs(TreeNode*node, string s){
if(s.size()!=0)s+="->";
s+=to_string(node->val);
if(!node->left && !node->right) res.push_back(s);
if(node->left)dfs(node->left,s);
if(node->right)dfs(node->right,s);
}
vector<string> binaryTreePaths(TreeNode* root) {
string now = "";
dfs(root,now);
return res;
}
★ 572. 另一棵树的子树 ★★★★
等左开KMP再来看吧. leetcode
树上的KMP
树的哈希?
112. 路径总和
坑有点多...
直接递归, 必须判断当前点是不是叶子, 然后当前的值和tagetsum相同不
bool hasPathSum(TreeNode* root, int targetSum) {
if(!root) return false;
if(!root->left && !root->right) return root->val == targetSum;
return hasPathSum(root->left,targetSum-root->val) ||
hasPathSum(root->right, targetSum-root->val);
}
上一题怎么把总数都求出来呢?
简单改一下就好了..
617. 合并二叉树
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if (!t1) return t2; // 这里注意, 不用执着返回t1;
if (!t2) return t1;
t1->val += t2->val;
t1->left = mergeTrees(t1->left, t2->left);
t1->right = mergeTrees(t1->right, t2->right);
return t1;
}
700. BST の 搜索
非常简洁的迭代了吧, 以后可能经常用.
TreeNode* searchBST(TreeNode* root, int val) {
while(root){
if(root->val < val) root = root->right;
else if(val < root->val) root = root->left;
else return root;
}
return NULL;
}
98. 验证是否是BST
带一个判定值的中序遍历, v
long long valnow = LONG_MIN; //这样子有错...
bool isValidBST(TreeNode* root) {
if(root==NULL) return true;
bool left = isValidBST(root->left);
if(valnow < root->val) valnow = root->val;
else return false;
bool right = isValidBST(root->right);
return left&&right;
}
TreeNode * pre = NULL; //改成存储一个先前节点就好了..
bool isValidBST(TreeNode* root) {
if(root==NULL) return true;
bool left = isValidBST(root->left);
if(pre!=NULL && pre->val >= root->val) return false; //这里判断
pre = root;
bool right = isValidBST(root->right);
return left&&right;
}
530. 二叉搜索树的最小绝对差
int res = INT_MAX;
TreeNode* pre = NULL;
void dp(TreeNode* t){
if(!t) return;
dp(t->left);
if(pre!=NULL)
res = min(res, t->val - pre->val); //直接取较小, 因为搜索树有序.
pre = t;
dp(t->right);
}
int getMinimumDifference(TreeNode* root) {
dp(root);
return res;
}
501. BST の 众数
这个先序遍历那里条件不太好写..
vector<int> res;
int maxcnt = 0, cnt = 1, val = INT_MIN;
void dp(TreeNode* root){
if(!root) return;
dp(root->left);
// 把判断val和cnt的提前, 这样才不会出错 ...
if(val == root->val) cnt++;
else cnt = 1, val = root->val;
if(cnt == maxcnt){res.push_back(val);}
else if (cnt>maxcnt) {res = {val}, maxcnt=cnt; }
dp(root->right);
}
vector<int> findMode(TreeNode* root) {
dp(root);
return res;
}
236. 二叉树的最近公共祖先
这个递归真的好绕啊..
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == q || root == p || root == NULL) return root;
auto left = lowestCommonAncestor(root->left, p, q);
auto right = lowestCommonAncestor(root->right, p, q);
if(left != NULL && right != NULL) return root;
if(left == NULL) return right;
return left;
}
235. BST の 最近公共祖先
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
// 这种直接判断 是否全大于 是否全小于, 可以避免交换 p 和 q;
// 因为可能有 p-val < q->val;
if(root->val <p->val && root->val < q->val) {
return lowestCommonAncestor(root->right, p, q);
}else if(root->val > p->val && root->val > q->val) {
return lowestCommonAncestor(root->left, p, q);
}else return root;
}
701. BST の 插入
TreeNode* insertIntoBST(TreeNode* root, int val) {
if(root == NULL) return new TreeNode(val);
if(root->val < val)
root->right = insertIntoBST(root->right, val);
else
root->left = insertIntoBST(root->left, val);
return root;
}
450. BST の 删除★★★★
TreeNode* deleteNode(TreeNode* root, int key) {
if (root == NULL) return root;
if (root->val == key){
if( !root->left && !root->right ) return NULL;
else if( !root->left) return root->right;
else if( !root->right) return root->left;
else{
auto cur = root->right;
while(cur->left!=NULL) cur = cur->left;
cur->left = root->left;
return root->right;
}
}
if(root->val > key) root -> left = deleteNode(root->left, key);
if(root->val < key) root -> right = deleteNode(root->right, key);
return root;
}
669. 修剪BST min和max
已经是最优的代码了... 可是递归的正确性真是个老大难的题.....
TreeNode* trimBST(TreeNode* root, int low, int high) {
if(root == NULL) return NULL;
if(root->val<low) return trimBST(root->right, low, high);
if(root->val>high) return trimBST(root->left, low, high);
root->right = trimBST(root->right, low, high);
root-> left = trimBST(root->left, low, high);
return root;
}
108. 构造BST
这个递归代码..
TreeNode* sortedArrayToBST(vector<int>& nums) {
return f(nums,0,nums.size()-1);
}
TreeNode* f(vector<int>& nums,int l,int r){
if(l>r)return NULL;
int mi = l +(r-l)/2;
TreeNode* res= new TreeNode(nums[mi]);
res->left = f(nums,l,mi-1), res->right = f(nums,mi+1, r);
return res;
}
二叉树总结
这个写的不错.
回溯
- 组合问题:
- 切割问题: 字符串有多少种切割方式.
- 子集问题:
- 排列问题
- 棋盘问题.
直接抽象成树的问题. 高度有限的N叉树.
void bt(...){
if (终止条件) {存放结果;return;}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
bt(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
动态规划
斐波那契:
f[n]=f[n-1]+f[n-2] f[0]=0 f[1]=1
746. 使用最小花费爬楼梯
dp数组表示到i个台阶需要多少话费dp(n+1)
//方法1
int dp[n+1]//: 用dp[i]表示到达第i个台阶花费,不包括第i个
dp[0]=0, dp[1]=0 //前两个可以随便到.
dp[i]=min(dp[i-2]+a[i-2], dp[i-1]+a[i-1]) //这个台阶可以跨1个或者2个上来.
return dp[n];
//方法2
int dp[n];//: 用dp[i]表示上了第i个台阶花费, 包括第i个.
dp[0]=cost[0], dp[1] = cost[1];
dp[i]=min(dp[i-1]+dp[i-2]) + cost[i];
return min(dp[n-1], dp[n-2]);
62. 不同路径
是一个组合问题 \(C^{m-1}_{m+n-2}\)
vector<vector<int>> dp(m,vector<int>(n));
dp[0][0] = 1;
for(int i = 0; i<m; i++){
for(int j =0; j<n; j++){
int&now =dp[i][j];
if(i) now+=dp[i-1][j];
if(j) now+=dp[i][j-1];
}
}
return dp[m-1][n-1];
63. 不同路径 II
障碍只要越过去就行了.
int uniquePathsWithObstacles(vector<vector<int>>& a) {
int n = a.size(), m = a[0].size();
vector<int> dp(m); // 滚动数组需要注意, 选择 m 而不是 n
dp[0] = !a[0][0]; // 需要判断初始点情况
for(int i=0; i<n; i++){
for(int j=0; j<m; j++){
if(a[i][j]) {dp[j]=0; continue;}
if(j>0) dp[j] += dp[j-1]; // 这里的递推关系还在.
}
}
return dp.back();
}
343. 整数拆分
拆分成至少两个整数.
其实只用考虑两种... j * (i - j) 和 j * dp[i-j]
//答案:
int integerBreak(int n) {
vector<int> dp(n+1); //用dp来代表答案: 分开至少两个后.
dp[2] = 1; // dp[0] dp[1] 都应该是 0;
for(int i = 3;i<= n;i++){
for(int j = 1;j<i-1;j++){ //这里j只循环到 i-2 因为 因为 i-j=1 没意义??
dp[i] = max(dp[i], max((i-j)*j,dp[i-j]*j));
}
}
return dp[n];
}
//原版:
int integerBreak(int n) {
vector<int> dp(n+1);
dp[1] = 1;
for(int i = 2;i<=n;i++){
int& ma = dp[i];
for(int j=1;j<i;j++){
ma = max(dp[i-j] * max(dp[j],j), ma);
if(j) ma=max((i-j)*j,ma);
}
}
print(dp);
return dp[n];
}
96. 不同的二叉搜索树
int numTrees(int n) {
vector<int> f(n+1);
f[1] = 1; f[0] = 1;
for(int i = 2; i<=n; i++){
for(int j = 0; j<i; j++){
f[i]+= f[j]*f[i-j-1];
}
}
// print(f);
return f[n];
}
背包专题.
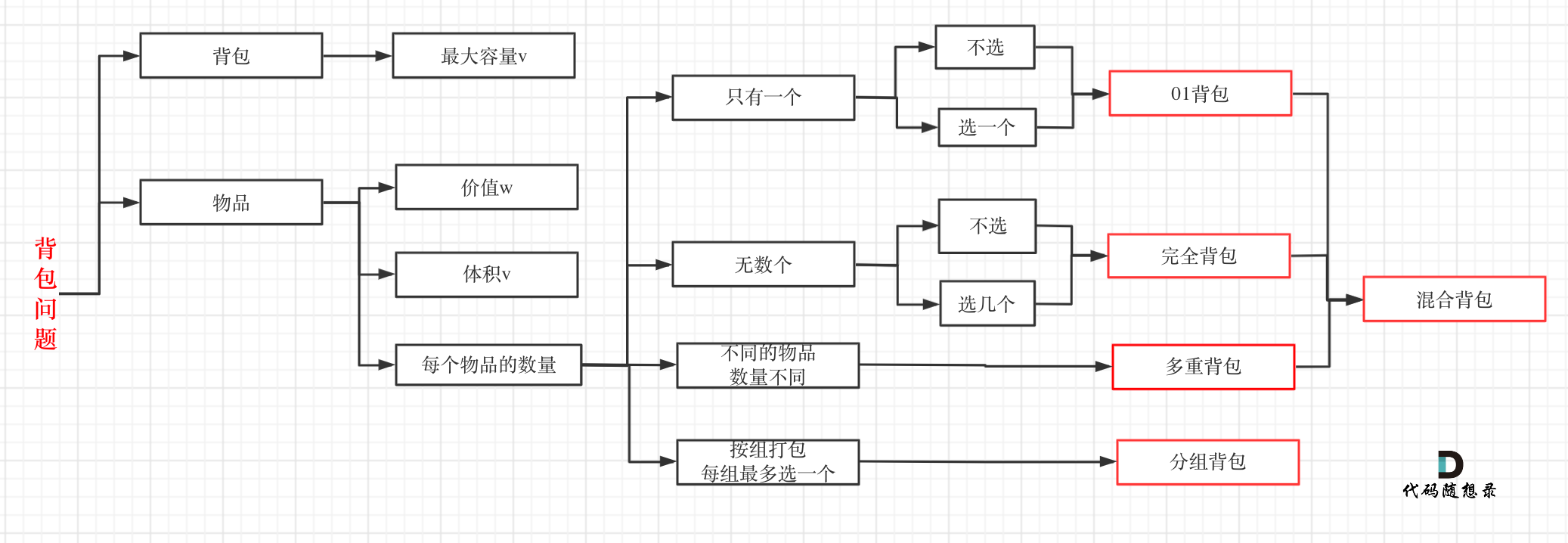
数量n 重量m w[i] v[i]
dp[i][j]在0-i的物品中随便取, 放进容量j的背包, 价值总和最大?- 不放物品
idp[i-1][j] - 放物品
idp[i-1][j-w[i]]+v[i] - 两者直接取max就是了.
- 不放物品
- 初始化 \(\forall i\)
dp[i][0]=0\FORALL jdp[0][j]=... - 遍历方向, 先物品, 再weight, 先weight 再物品都是可以的.
416. 分割等和子集
为什么np问题可以用 动态规划? 时间复杂度和元素大小相关?
背包重量恰好等于整个数组元素的一半.
bool canPartition(vector<int>& nums) {
int n = nums.size();
int sum = accumulate(nums.begin(), nums.end(), 0);
int maxNum = *max_element(nums.begin(), nums.end());
int target = sum /2;
if(n<2 || sum&1 || maxNum>target)
return false; //如果n<2或者sum是奇数或者max比target大, 都能直接返回false;
vector<bool> dp(target+1);
dp[0] = true;
for(int i = 0; i < n; i++){
int num = nums[i];
for(int j = target; j >= num; --j){
dp[j] = dp[j] || dp[j - num];
}
}
return dp[target];
}
1049. 最后一块石头的重量 II
2-sum 基础上 减去集合可以达到的小于 target的最大值就好了...
int lastStoneWeightII(vector<int>& a) {
int n = a.size();
int sum = accumulate(a.begin(), a.end(), 0);
int target = sum/2;
vector<int> f(target+1);
f[0] = true;
for(int i = 0;i<n;i++){
for(int j = target;j>=a[i];j--){
f[j] |= f[j-a[i]];
}
}
for(n = target;n>0;n--){
if(f[n])break;
}
// print(f);
return sum - 2 * n;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号