面向移动设备的真实感图形处理系统设计与实现

目录

• 绪论
  • 3D图形绘制管线
    • 应用程序部分
    • 几何部分
  • 光栅部分
  • 3D图形绘制架构的发展
  • 部分图形处理器的性能参数
• 理论基础
  • 几何部分
    • 模型到观察坐标系变换
    • 光照算法
      • 光的组成部分
      • 光源的种类
      • 物体的材质
      • 光照模型
    • 雾化因子计算
    • 投影变换
    • 视锥体裁剪和背向面剔除
      • 视锥体裁剪
      • 背向面剔除
    • 屏幕坐标变换
  • 光栅部分
    • 扫描转换与插值
      • 传统方法：两次插值
      • 半空间填充算法（边界函数法）
      • 基于平面方程的插值方法
      • 重心坐标插值法
      • 透视校正插值
    • 纹理贴图
      • 点采样法
      • 双线性滤波
      • Mip-Map
      • 三线性滤波
    • 反走样
    • 可见性测试
      • 深度缓冲(Z-Buffer）算法
• 几点想法

绪论

3D图形绘制管线

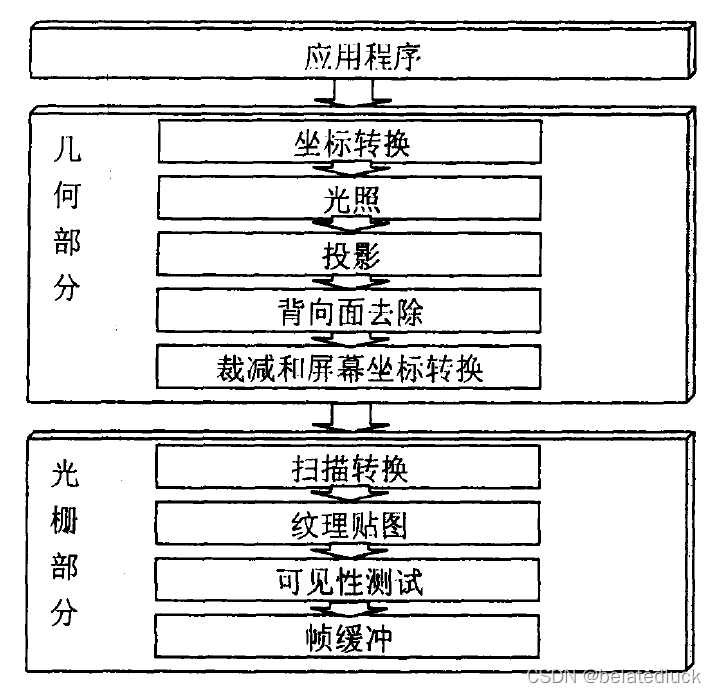
3D图形绘制管线一般由三大部分组成：

• 应用程序部分：通过软件方式实现，负责产生场景、改变场景参数或者获取其他的信息（键盘、鼠标输入等等），最终生成场景的图元序列送入到几何部分处理
• 几何部分：负责对多边形的定点进行操作，典型的操作包括坐标转换、光照和裁剪等
• 光栅部分：负责对多边形进行填充，并转换成2D屏幕可以显示的像素
  

应用程序部分

三维物体的表面通过三角面、线、点来近似，在进行处理时，只需要传送和计算三角面的顶点数据，三角面内部的数据可以通过线性插值得到

• 每个顶点包含的信息包括位置信息、法线信息、颜色信息以及纹理坐标等
• 由于顶点一般被许多三角面共用，因此，建立一个统一的顶点数组，场景中的三角面使用对该顶点数组的索引表来表示
• 顶点数组和三角面顶点索引表是应用程序部分的输出，是几何部分的输入
  

几何部分

在几何部分，三角面信息依次经过坐标变换、光照运算、投影变换、背向面去除、裁剪和屏幕坐标变换，获得视锥体（人眼看到的范围）之内的模型部分在屏幕坐标系下的信息。

• 坐标变换：首先，讲模型由局部坐标系下的顶点坐标转换到统一的世界坐标系下，然后再转换到观察坐标系下
• 光照运算：再观察坐标系下计算每个顶点发射或反射到人眼的光强
• 投影变换：将视锥体内的范围变换到一个规则的正方体中
• 背向面剔除：将物体背面观察不到的三角面剔除
• 裁剪：部分或者全部位于视锥体之外的三角形兼备裁剪，只保留位于视锥体之内的部分
• 屏幕坐标变换：将裁剪后的三角面转换到屏幕坐标系

光栅部分

光栅部分将屏幕上的三角面进行填充，形成屏幕上实际将要显示的画面信息写入到帧缓存中

• 扫描转换：生成位于三角面内部的像素点，并用线性插值的方法计算这些像素点的颜色
• 纹理贴图
• 可见性测试：剔除被遮挡的点
• 帧缓存：将通过可见性测试的点写入到帧缓存中（注：帧缓存中的内容将由显示控制电路读取并发送给屏幕，最终完成整个显示过程）

3D图形绘制架构的发展

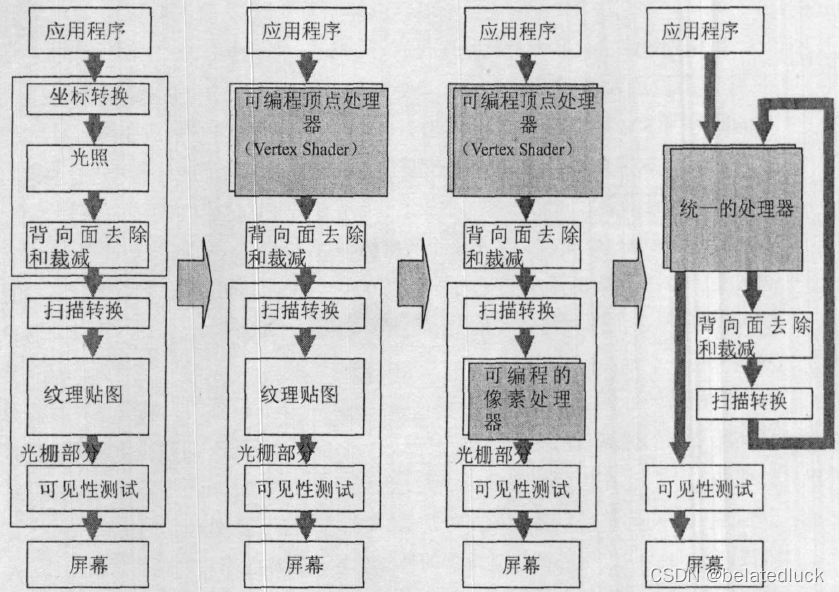
1. 固定功能的绘制架构：
2. 具有可编程顶点处理器的绘制架构：
3. 具有可编程顶点处理器和可编程像素处理器的绘制架构
4. 统一处理器架构

部分图形处理器的性能参数

• GoForce5500： 2.6M三角面/s， 200MPixel/s
• PowerVR MBX R-S：1.5M三角面/s，250MPixel/s
• Mali200：10M三角面/s，300MPixel/s

理论基础

几何部分

几何部分对应用程序送来的每个顶点或者每个三角面进行操作。几何部分将场景中各个模型的顶点和法线（有时还包括纹理坐标）进行矩阵变换并将模型放到观察空间中；根据物体的材质、纹理以及光源的属性等参数计算顶点的光照；根据物体距离眼睛的远近计算雾化因子；然后将位于观察空间中的模型进行投影变换，变换到一个单位的立方体；然后进行裁剪操作，舍弃所有在单位立方体之外的图元；最后将裁剪后的图元映射到屏幕上面，并进行简单的背向面判断后送入光栅阶段。
其中，光照阶段的计算量最大。在单光源的情况下，精确计算每个顶点的光照需要约100次浮点运算，坐标变换和投影变换每次变换每个顶点需要约16次乘法运算和12次加法运算。如果有6个裁减面，每个三角面需要约36次乘法运算，但实际场景中需要裁减的三角面所占比例很小。

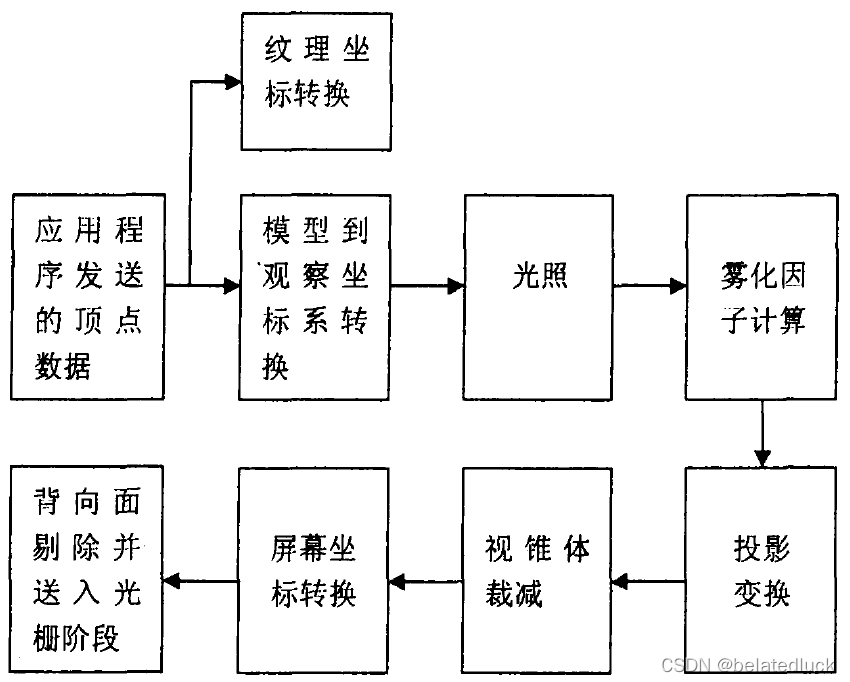
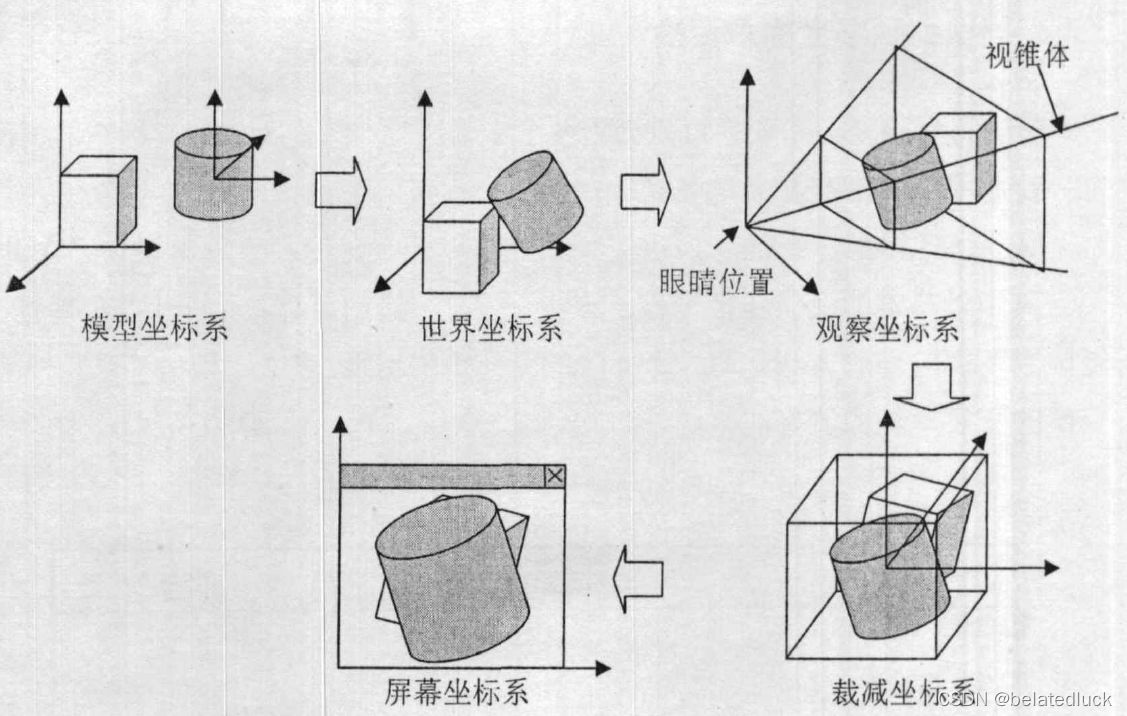
几何部分使用到的几种坐标系有：

• 模型坐标系：单一模型使用的局部坐标系
• 世界坐标系：场景的坐标系，为其内所有三维模型公用
• 观察坐标系：以眼睛为原点，观察方向为Z轴方向，上方为Y轴方向的坐标系
• 裁减坐标系：将视锥体通过透视投影或者平行投影映射为一个单位立方体，以便于裁减运算，映射后的坐标系称为裁减坐标系
• 屏幕坐标系：以屏幕的某个点（如左下角）为原点的二维坐标系，需要注意的是，转换到屏幕坐标系后，深度信息必须保留以用于遮挡判断
  
  引入齐次坐标的概念以进行坐标变换。将一个n维向量（例如，对三维向量\(P=[x,y,z]\)）扩展到n+1维（四维向量\(P'=[x,y,z,w]\)），其中\(w\)称为齐次因子。坐标系的所有变换都可以通过齐次坐标乘一个矩阵来实现，称该矩阵为齐次变换矩阵。假设变换前的点为\(P(x,y,z,1)\)，变换后的点为\(P'(\frac{x'}{w},\frac{y'}{w},\frac{z'}{w},1)\)，其齐次坐标为\((x',y',z',w)\)，变换矩阵为\(T=\begin{bmatrix} a & b & c & p \\ d & e & f & q \\ g & h & i & r \\ l & m & n & s \end{bmatrix}\)，则有

\[P'=TP=\begin{bmatrix} a & b & c & p \\ d & e & f & q \\ g & h & i & r \\ l & m & n & s \end{bmatrix} \cdot \begin{pmatrix}x \\ y \\ z \\ 1 \end{pmatrix} = w \begin{pmatrix} \frac{x'}{w} \\ \frac{y'}{w} \\ \frac{z'}{w} \\ 1 \end{pmatrix} \\ \]

且，

\[\begin{pmatrix} x' \\ y' \\ z' \end{pmatrix} =\begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \cdot \begin{pmatrix}x \\ y \\ z \end{pmatrix} + \begin{pmatrix} p \\ q \\ r \end{pmatrix} \\ \begin{pmatrix} l \\ m \\ n \end{pmatrix} \cdot \begin{pmatrix} x \\ y\\ z \end{pmatrix} + s = w \]

因此，矩阵\(T\)包含了4个子矩阵：3x3矩阵\(\begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}\)的作用是产生局部比例、反射、旋转、错切边换，3x1矩阵\(\begin{bmatrix} p \\ q \\ r \end{bmatrix}\)的作用是平移，1x3矩阵\(\begin{bmatrix} l & m & n \end{bmatrix}\)的作用是投影变换，1x1矩阵\(\begin{bmatrix}s\end{bmatrix}\)的作用是产生整体比例变换。
典型的变换矩阵如下：

变换类型	变换矩阵	说明
绕\(x\)轴旋转	\(\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos\theta & -sin\theta & 0 \\ 0 & sin\theta &cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\)	绕\(x\)轴旋转角度\(\theta\)
绕\(y\)轴旋转	\(\begin{bmatrix} cos\theta & 0 & sin\theta & 0 \\ 0 & 1 & 0 & 0 \\ -sin\theta & 0 & cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\)	绕\(y\)轴旋转角度\(\theta\)
绕\(z\)轴旋转	\(\begin{bmatrix} cos\theta & -sin\theta & 0 & 0 \\ sin\theta &cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\)	绕\(z\)轴旋转角度\(\theta\)
缩放	\(\begin{bmatrix} S_x & 0 & 0 & 0 \\ 0 & S_y & 0 & 0 \\ 0 & 0 & S_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\)	分别对\(x,y,z\)轴缩放\(S_x, S_y, S_z\)

模型到观察坐标系变换

模型到世界坐标系变换决定一个物体在场景中出现的位置和角度，其中基本的变换包括平移、旋转、缩放、错切等等。
世界坐标系到观察坐标系的转换本质上也是平移和旋转变换的组合。首先先确定观察者位置\(p\)、观察的方向\(n\)和指向观察者上方的向量\(v\)，如果\(v\)与\(n\)不垂直则把\(v\)变为与\(n\)垂直的分量，然后对坐标系进行平移和旋转，令\(p\)位于原点，\(n\)指向\(z\)轴正向，\(v\)指向\(y\)轴正向。另外，由于观察坐标系为左手系，世界坐标系为右手系，因此最后需要将\(z\)轴方向。

光照算法

光照算法计算从物体表面反射出来进入人眼的光的亮度，其取决于光源的位置、光强、物体的材质、物体的表面法线以及视点的位置。

光的组成部分

人眼看到的光分为反射光、透射光和辐射光。其中，反射光又分为泛光、漫反射光和镜面反射光。

• 泛光用来模拟从周围环境中物体散射到物体表面再反射出来的光，也称为环境光
• 漫反射光是物体反射光中向空气均匀反射的光，反射的光强与入射光的入射角的余弦成正比，当光线垂直于物体表面时，物体最亮
• 镜面反射光是朝一定方向反射的光，可形成高光效果

光源的种类

光源可分为平行光、点光、聚光三种。

• 平行光源位于无穷远处，来自光源的光线都是互相平行的
• 点光源位于空间的某个位置，向四周辐射光线
• 聚光源是特殊的点光源，它仅仅在一个椎体中发射光线
  关于光源的参数一般有四个：环境光强度颜色\(s_{amb}\)、漫反射光强度颜色\(s_{diff}\)、镜面反射光强度颜色\(s_{spec}\)，以及光源的位置\(s_{pos}\)。

物体的材质

物体的材质是指物体表面对光的反应特性，通常分为反射性能、透射性能、吸收性能三种，一般最重要的是反射性能。反射性能由环境颜色\(m_{amb}\)、漫反射颜色\(m_{diff}\)以及镜面反射颜色\(m_{spec}\)等组成，分别表示物体对环境光、漫反射光和镜面反射光的反射强度。此外还有高光系数\(m_{shi}\)表示镜面反射光在空间中的聚集程度（光滑度？），自发光颜色\(m_{emb}\)表示放射性材质本身发射的光线颜色。

光照模型

光照模型分为局部光照模型和整体光照模型。局部光照模型进考虑光源直接照射在物体表面所产生的的效果，而物体表面通常被假定为不透明，且具有均匀的反射率。整体光照模型除了上述因素外，还考虑周围环境对物体表面的影响。
局部光照模型能表现出由光源直接照射在漫射表面上形成的连续明暗色调、镜面上的高光以及由于物体互相遮挡而形成的阴影。整体光照模型能够模拟出镜面映像、光的折射以及相邻表面之间的色彩辉映等较精确的光照明效果。
在实时图形学中，往往只考虑局部光照模型，其中最典型的是Phong光照模型。在Phong光照模型下，物体表面最终的光照\(I\)由三个分量组成，分别是环境分量\(I_{amb}\)、漫反射分量\(I_{diff}\)和镜面反射分量\(I_{spec}\)，即\(I=I_{amb}+I_{diff}+I_{spec}\)。
只考虑一个泛光源的情况下，有

\[I_{amb} = m_{amb} \otimes S_{amb} \\ I_{diff} = max((n \cdot l),0) m_{diff} \otimes S_{diff} \\ I_{spec} = max((r \cdot v),0)^{m_{shi}} m_{spec} \otimes S_{spec} \]

其中\(n\)为物体表面被照射处的单位法向量，\(l\)为被照射点到光源的单位向量，\(r\)为光线经法向量反射后光线方向的单位向量，\(v\)为被照射点指向摄像机位置的单位法向量。
考虑光的衰减的情况下，有

\[I=I_{amb} + f(I_{diff} + I_{spec}), f=\frac{1}{C_0+C_1d+C_2d^2} \]

其中，\(f\)为衰减因子，\(d\)为光源到物体顶点的距离，\(C_0\)控制固定衰减，\(C_1\)控制线性衰减，\(C_2\)控制二次衰减。
当考虑多个光源及物体自发光的情况下，引入全局光源参数\(a_{glob}\)表示来自周围的恒定环境光，假设光源数量为\(N\)，有

\[I_{total}=a_{glob} \otimes m_{amb} + m_{emi} + \sum_{i=1}^{N}(I_{amb}'+f(I_{diff}'+I_{spec}')) \]

当光源数量增加时，需要注意避免颜色因叠加而溢出，在光栅绘制的时候，需要将颜色归一化。

雾化因子计算

雾化有三个作用，第一，提高真实感；第二，由于远处的雾看起来更浓，可以帮助观察者判断物体的距离；第三，在远平面裁剪中，某些远处的物体会被突然裁掉，雾化可以掩盖物体突然消失的不自然。
用雾化因子来表示雾的浓淡，雾化因子越小表示雾越浓。计算雾化因子一般有三种模式：

• 线性雾化模式：雾化因子随距离的增加而线性递减，该模式有两个参数，雾化效果开始和终止的位置\(z_{start}\)和\(z_{end}\)，假设物体顶点的深度值为\(z\)时，雾化因子\(f=\frac{z_{end}-z}{z_{end}-z_{start}}\)
• 指数雾化模式：雾化因子随着距离增加而指数衰减，\(f=e^{-d_fz}\)，其中\(d_f\)控制雾化衰减速度
• 指数平方模式：雾化因子随着距离增加而指数平方衰减，\(f=e^{-(d_fz)^2}\)
  计算出雾化因子\(f\)后，假设雾化颜色\(c_f\)，经着色处理的物体表面颜色是\(c_s\)，那么像素最终的颜色\(c_p=fc_s+(1-f)c_f\)

投影变换

投影变换将视锥体内的物体投影到一个单位正方体，即观察坐标系到裁减坐标系的转换，以便于裁减。投影可分为平行投影和透视投影两种。平行投影物体的大小和距离无关，适合CAD设计等场合，而透视投影物体近大远小，适合真实感图形的绘制。
假设用\((left, right, bottom, top, near, far)\)表示视锥体的六个屏幕，则平行投影的转换矩阵有

\[T= \begin{bmatrix} \frac{2}{right-left} & 0 & 0 & -\frac{right+left}{right-left} \\ 0 & \frac{2}{top-bootom} & 0 & -\frac{top+bottom}{top-bottom} \\ 0 & 0 & \frac{2}{far-near} & -\frac{far+near}{far-near} \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

透视投影的转换矩阵有

\[T= \begin{bmatrix} \frac{2 \times near}{right-left} & 0 & -\frac{right+left}{right-left} & 0 \\ 0 & \frac{2 \times near}{top-bootom} & -\frac{top+bottom}{top-bottom} & 0 \\ 0 & 0 & \frac{far+near}{far-near} & -\frac{2 \times far \times near}{far-near} \\ 0 & 0 & 1 & 0 \end{bmatrix} \]

两种投影都将视锥体映射到单位立方体中，近平面到\(z=-1\)，远平面到\(z=1\)，左平面到\(x=-1\)，右平面到\(x=1\)，下平面到\(y=-1\)，上平面到\(y=1\)。在透视投影下，近平面上透视引入的缩放为1，远平面上为\(\frac{n}{f}\)。

视锥体裁剪和背向面剔除

视锥体裁剪

如果图元完全位于视锥体之外，则直接剔除；如果恰好跨越了视锥体边界，这需要剔除位于视锥体之外的部分。在裁剪坐标系下，六个裁剪平面为\(x=1,x=-1,y=1,y=-1,z=1,z=-1\)，对应的齐次坐标为\(x_h=w_h,x_h=-w_h,y_h=w_h,y_h=-w_h,z_h=w_h,z_h=-w_h\)。在进行裁剪是，首先对三角面的三条边分别进行裁剪，确定线段与裁剪平面的交点，并插值计算出交点包含的诸如颜色、雾化因子、纹理坐标等信息，然后以三角面扇形的方式对三角面在视锥体内的部分进行重新分割。

背向面剔除

视锥体裁剪有两种方法：①在观察坐标系下判断三见面法线与定点到视点向量的点积，如果为负则是背向面；②在观察坐标系下判断三角面的法向量的\(z\)的符号，如果为正则为背向面。一般会采取第二种方法，因为如果采用第一种方法，对于某些在临界角度的图元，有可能因为观察坐标系到裁减坐标系的变换中的计算误差引起观察坐标系下是背向面而裁减坐标系下不是的情况，如果光栅部分没有对这样的图元进行特殊处理，就会引起绘制错误，此外，投影模式会影响背向面的计算也是不采用第一种方法的原因。

屏幕坐标变换

屏幕映射将单位立方体的图元映射到屏幕或者窗口。首先，将齐次坐标转换为三维坐标，

\[x=\frac{x_h}{w_h},y=\frac{y_h}{w_h},x=\frac{z_h}{w_h} \]

然后将裁剪坐标系的三维坐标映射到屏幕区间内，假设屏幕宽\(s_w\)，高\(s_h\)，有

\[x_{scr}=\frac{1}{2} (x+1) \times s_w \\ y_{scr}=\frac{1}{2} (y+1) \times s_h \\ z_{scr}=\frac{1}{2}(z+1) \]

光栅部分

几何部分对图元的顶点进行处理，而光栅部分对图元内的像素进行处理。

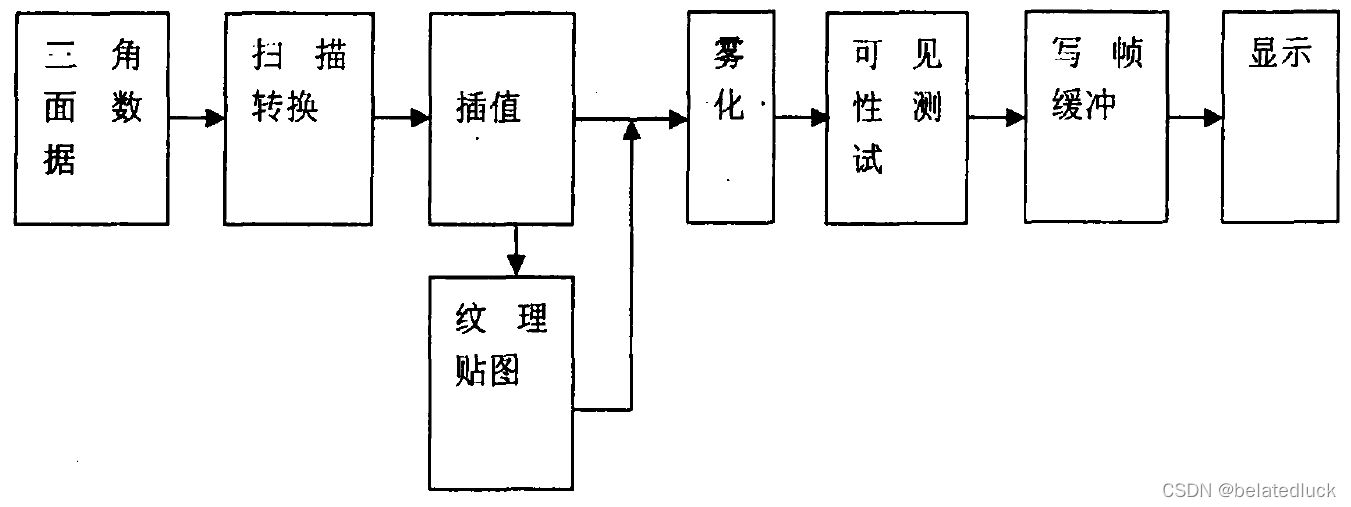
几何部分给光栅部分的输入包括顶点坐标、颜色、雾化因子、纹理坐标等，这些被扫描转换单元扫描处理，产生三角面覆盖的每一个像素位置，然后送入插值单元进行插值，计算出每个像素的属性值；然后纹理坐标被送入纹理贴图单元，纹理单元返回的纹理颜色会与光照颜色混合；混合颜色送入雾化单元进行雾化混合得到最终的颜色；可见性测试判断像素是否可见，可见的像素颜色被送入帧缓冲，完成光栅部分过程。

扫描转换与插值

扫描转换时通过某种顺序将三角面覆盖的像素遍历一遍，关键在于判断像素是否在三角面之内，并插值求出三角面的像素属性。

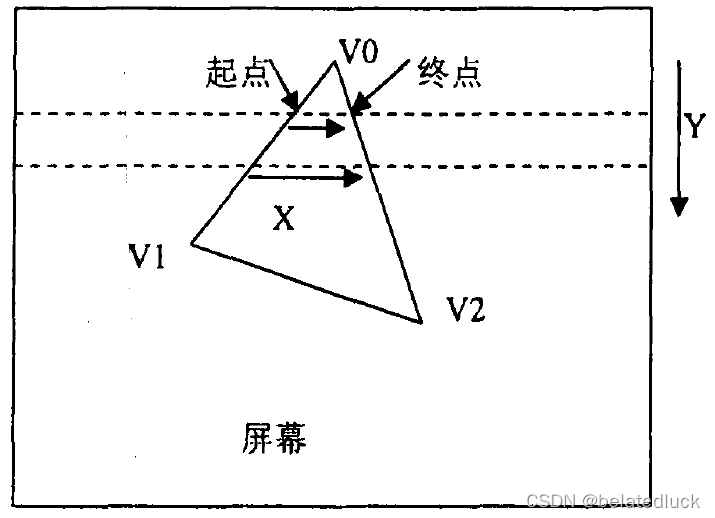
传统方法：两次插值

最直观的，首先在\(y\)方向扫描，得出每条水平扫描线与三角面边界的交点，即起点和终点，并插值求出交点的属性，然后在\(x\)方向扫描，根据起点和终点的属性计算中间每一个像素的属性。（关于为什么要两次扫描，可以了解下Bresenham算法，这是为了避免浮点计算）

半空间填充算法（边界函数法）

假设线段的端点为\(P(x_0,y_0)\)与\(P'(x_1,y_1)\)，线段方向为\(P->P'\)，则对于该线段，点\((x,y)\)的边界函数为

\[e(x,y)=ax+by+c \\ 其中，a=y_0-y_1，b=x_1-x_0,c=x_0y_1-x_1y_0 \]

当\(e(x,y)>0\)的时候，说明点在线的左侧,当\(e(x,y)<0\)的时候，说明点在线的右侧,当\(e(x,y)=0\)的时候，说明点在线上。对于逆时针排列的三角面，如果点对其三条边的边界函数都大于0，那么点在三角面内。
对于在三角面边界上的点，不能简单都抛弃或者都保留，因为三角面之间会共用边。可以设定一个规则让共用边的三角形只有一个会保留该边上的点。设边的法线为\(n=(a,b)\)，判据为

\[t=(a>0)||(a==0 \&\& b>0) \]

接下来，就可以通过判据进行扫描确认在三角面内的点。

基于平面方程的插值方法

通过三角面计算出属性和坐标方程的系数，然后在进行边界扫描是用坐标来计算属性值。这种方法中参数的误差会被相对较大的坐标值放大，因此要求参数的精度要高，而且参数的位宽不确定，要求硬件设计使用较大的数据位宽。

重心坐标插值法

假设三角面\((v_0,v_1,v_2)\)分别拥有属性\((s_0,s_1,s_2)\)，则三角面内任意一点\(P\)的属性\(s\)有

\[s=\frac{A_0}{A_\Delta}s_0+\frac{A_1}{A_\Delta}s_1+\frac{A_2}{A_\Delta}s_2 \]

其中\(A_0,A_1,A_2\)分别为\(P\)点与三角面三个顶点围成的区域的面积，\(A_\Delta\)为三角面的总面积。将参数定义为插值系数：

\[(k_0,k_1,k_2)=\frac{(A_0,A_1,A_2)}{A_\Delta} \]

有

\[s=k_0s_0+k_1s_1+k_2s_2 \\ =(1-k_1-k_2)s_0+k_1+k_2s_2 \\ =s_0+k_1(s_1-s_0)+k_2(s_2-s_0) \]

代入

\[A_0=\frac{1}{2}((x-x_2)(y_1-y_2)-(y-y_2)(x_1-x_2)) \\ A_1=\frac{1}{2}((x-x_0)(y_2-y_0)-(y-y_0)(x_2-x_0)) \\ A_2=\frac{1}{2}((x-x_1)(y_0-y_1)-(y-y_1)(x_0-x_1)) \]

及边界函数定义得

\[k_1=\frac{e_1(x,y)}{2A_\Delta},k_2=\frac{e_2(x,y)}{2A_\Delta} \]

因此，只要在三角形建立阶段计算出\(\frac{1}{2A_\Delta}\)，即可直接使用边界函数计算各个属性的插值。
由于像素属性位宽一般较小，因此这种方法使用的乘法器位宽会比较低。

透视校正插值

实际上，透视投影会破坏像素属性和坐标之间的线性关系，对于要求不高的场合，颜色属性可以直接使用线性插值得到，但是对于纹理坐标\((u,v)\)，必须采用透视校正插值，否则可能会产生明显失真。
透视校正插值方法先算出属性\(s\)与齐次因子\(w\)的商\(\frac{s}{w}\)，然后对\(\frac{s}{w}\)和\(\frac{1}{w}\)分别进行线性插值，最后将前者除以后者得到透视校正后的插值。该方法需要每个像素计算一次除法，计算量较大。

纹理贴图

纹理一般可分为两种，颜色纹理和几何纹理。
纹理贴图是将纹理图片的颜色覆盖到屏幕上的像素上去的过程。纹理图片上的像素称为纹素，屏幕上的像素称为像素。纹理坐标\((u,v)\)确定了纹素和像素的对应关系。
需要注意的是，纹理本身是一种具有一定频率的信息，当像素对应的纹理坐标的采样密度太低时，会导致纹理走样。

点采样法

使用纹理坐标最接近的纹素颜色作为纹理坐标对应的颜色。该方法会有明显的走样出现。

双线性滤波

在纹理映射期间，考虑距离纹理坐标最近的相邻的4个纹理元素，然后在二维空间中进行线性插值得到使用的纹理值。有

\[C(u,v)=(x+1-u)(y+1-v)C(x,y)+(u-x)(y+1-v)C(x+1,y)+(x+1-u)(v-y)C(x,y+1)+(u-x)(v-y)C(x+1,y+1) \]

双线性滤波会使得纹理颜色过渡更平滑，但是仍会面临走样问题。

Mip-Map

Mip-Map的含义是分级细化映射，首选in对纹理图像进行预处理，生成一组分辨率逐渐缩小的图像，然后在纹理映射过程中，对离观察者较近的大物体采用高分辨率的纹理图像，而对距离观察者较远的小物体，采用分辨率更小更模糊的纹理图像，用纹理细节层次\(l\)来表示，对于分辨率从大到小的纹理图像，\(l\)从0开始逐渐递增。
在纹理图像选择时，首先计算纹理锁表两个分量在像素空间的两个方向的变化率，求得纹素尺寸与像素尺寸之比\(r\)，则选择的纹理层次\(l=log_2r\)，\(l\)非整数时，取\(round(l)\)。

三线性滤波

三线性滤波法结合了双线性插值法和Mip-Map算法，且当\(l\)为小数时，首先采用双线性插值在最近的两层计算出纹理值，然后使用\(l\)再进行线性插值。但是，三线性插值对硬件和带宽有更高的要求。

反走样

扫描转换、插值、纹理贴图本质上都是采样过程，用离散的像素采样连续的3D场景或者纹理图片，因此无法避免锯齿状失真，一般称为走样（Aliasing）。反走样（Anit-Aliasing）有基于屏幕的反走样和基于图元的反走样。后者典型的是纹理反走样和直线反走样。基于屏幕的反走样技术一般采用多个采样对对同一个像素进行采样，最后将这些采样点的颜色按照一定的权重混合起来，即

\[p(x,y)=\sum_{i=1}^{n}w_ic(i,x,y) \]

其中\(p\)是像素的颜色，\(n\)为采样点的数目，\(w_i\)为第\(i\)个采样点的权重，\(c\)是采样点的颜色。
常用的全屏反走样方法有

• 超采样方法：在一个像素内分布多个采样点，从而对一个像素进行多次采样，典型的采样点分布方法有2x1网格、1x2网格、2x2网格、2x2旋转网格（RGSS）、五点梅花（Quincunx）、FLIPQUAD等。也可以通过绘制一幅更高分辨率的图像最后再进行混合来实现（Full-Scene Anti-aliasing,FSAA）。
• A缓冲器法：主要用于边缘反走样，计算每个像素被三角面近似覆盖的面积，最后再把所有的片段混合起来。这种方法比较复杂，不适合硬件实现。

可见性测试

在OpenGL绘制流程中，可见性测试可能包括深度测试、模板测试以及Alpha测试等。
测度测试通过像素的空间关系来判断其是否可见。
模板测试中，前面的三角面可以留下某些记号，后面的三角形根据记号来决定是否可见。
Alpha测试测试像素的Alpha值是否符合设定的要求。

深度缓冲(Z-Buffer）算法

如果三角面上的点被投影到屏幕上的同一像素，则只有深度值最小的面片上的点才会最终显示在屏幕上。具体实现来讲，需要建立一个和屏幕一样大小的缓冲器Z-Buffer，在开始绘制的时候将其初始化为最大值，然后对三角面内每一像素进行绘制，判断\(z\)值是否小于Z-Buffer内响应的\(z\)值，如果是就将像素的颜色写入帧缓冲，否则丢弃这个像素。

几点想法

1. 透视变换实际上仅考虑了\(z\)坐标，没有考虑实际距离，原因可能是为了采用线性变换
2. 观察坐标系采用左手系，原因在于为了与屏幕坐标系保持一致，从屏幕来看，水平向右为\(x\)轴，垂直向上为\(y\)轴，而深度向前为\(z\)轴
3. 屏幕坐标系下实际上认为人在无穷远处，因此，人眼的移动不影响显示的内容?
4. 光照为什么在几何阶段完成