第六章 NURBS曲线
众所周知,工业产品的形状大致可分为两类或由这两类组成,一类仅由初等解析曲线曲面如二次曲线、二次曲面等组成。大多数机械零件属于这一类,可以用画法几何与机械制图完全表达清楚和传递所包含的全部形状信息。第二类是不能由初等解析曲线曲面组成,而是由以复杂方式自由地变化的曲线曲面组成—即 所谓的自由型曲线曲面。例如象飞机、汽车、船舶等的外形零件。显然,这后一类曲线曲面不能单纯用画法几何与机械制图完全表达清楚,而必须采用参数多项式样条曲线曲面方法。由于这两种类型的曲线曲面其数学上的表示完全不同,这就给CAD/CAM系统的开发与研制带来困难和麻烦。
一个商品化的CAD/CAM系统应能满足工业设计的各种需求,无论什么类型的曲线曲面都能精确表示。由于参数多项式样条曲线曲面无法精确表示除抛物线外的初等解析曲线曲面,只能近似地逼近,因此若采用参数多项式曲线曲面作为几何造型的工具,则使得外形的设计"精度"大大降低。因为对CAD/CAM而言,除了计算机数值表示引起的误差外,形状的表示应当是精确的。而采用参数多项式样条曲线曲面和初等解析曲线曲面的混合模型,由于这两类方法数学表示上的不统一,则给编程带来了麻烦。进而,采用混合模型的CAD/CAM系统会随着所处理几何元素的增加,其所需的时间与空间幂次增加。对于采用单一模型的CAD/CAM系统,这种计算量的增加只是线性的。因此,为了建立一种既能包含参数多项式样条曲线曲面,又能精确表示初等解析曲线曲面的单一几何模型,人们提出了新的曲线曲面表示与设计方法,这就是NURBS曲线曲面。
最早尝试在几何形状设计中使用NURBS曲线曲面方法的是Boeing公司的Rowin'64和MIT的Coons'67,就其应用而言,他们的主要兴趣是把二次曲线和参数三次多项式曲线统一到参数有理三次曲线之中,以解决前两种曲线因算式不统一而引起的编程麻烦。而真正面向CAD/CAM实际应用的研究则始于美国SDRC(Structure Dynamics Research Corporation)的Till'83,他是第一位采用NURBS曲线曲面方法解决曲线曲面的表示和设计问题的,并将其用于该公司的GEOMOD系统和I-DEAS系统之中。
鉴于NURBS技术在形状定义方面的强大功能和潜力,不等该技术完全成熟,美国国家标准局在1983年制订的初始图形交换规范IGES(Initial Graphics Exchange Specification)第二版中就将NUTBS列为优化类型。1988年颁布的产品定义交换规范STEP/PDES(1.0版)只规定了惟一的一种自由型参数曲线曲面,即NURBS。1991年国际标准化委员会正式颁布了工业产品数据交换于表达的国际标准STEP。在STEP中,NURBS作为定义工业产品几何形状的惟一数学方法。
6.1 参数有理曲线
6.1.1 参数有理曲线的定义
参数有理多项式曲线曲面方法是参数多项式曲线曲面的直接推广。从数学角度看,它的定义以齐次坐标为基础,即用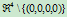 中的点表示
中的点表示 中的点。
中的点。
齐次坐标
对于点 ,它的齐次坐标
,它的齐次坐标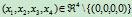 是满足关系
是满足关系
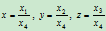 (6.1.1)
(6.1.1)
的四元有序组。如果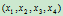 是
是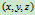 的齐次坐标,那么对任意非零常数
的齐次坐标,那么对任意非零常数 ,四元有序组
,四元有序组 亦是
亦是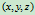 的齐次坐标。
的齐次坐标。
显然,要使式(6.1.1)有意义,必有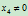 。而当
。而当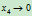 时,点
时,点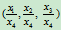 沿向径
沿向径 方向趋于无穷远。因而,点
方向趋于无穷远。因而,点 表示了向径
表示了向径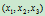 方向上的无穷远点,该点可用
方向上的无穷远点,该点可用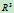 中的方向矢量
中的方向矢量 表示之。
表示之。
式(6.1.1)的本质是一个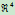 的原点到超平面
的原点到超平面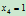 的透视映射
的透视映射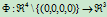
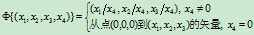 (6.1.2)
(6.1.2)
因此,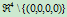 中任一点在
中任一点在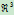 中都有惟一的映射像,它或者是
中都有惟一的映射像,它或者是 中的点,或者是
中的点,或者是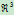 中的一个向量。反之,
中的一个向量。反之, 中任一点
中任一点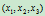 都是
都是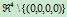 中一点的映射像,例如
中一点的映射像,例如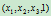 就是,一般地有
就是,一般地有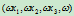 (
(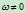 )。
)。
基于这一讨论,我们便可用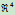 中的参数多项式曲线来定义
中的参数多项式曲线来定义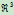 中的参数有理多项式曲线,其中应用最广泛的参数有理多项式曲线有有理Bézier曲线和NURBS曲线两种,下面分别给出其定义。
中的参数有理多项式曲线,其中应用最广泛的参数有理多项式曲线有有理Bézier曲线和NURBS曲线两种,下面分别给出其定义。
定义6.1
在射影空间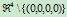 中给定
中给定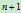 个点
个点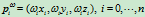 ,则一条参数
,则一条参数 次的有理Bézier曲线定义为下述的参数
次的有理Bézier曲线定义为下述的参数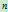 次有理多项式矢值函数:
次有理多项式矢值函数:
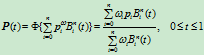 (6.1.3)
(6.1.3)
其中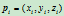 称为曲线
称为曲线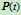 的Bézier点,
的Bézier点,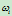 称为权因子。实际应用中,为了保证曲线不出现渐近线,通常取
称为权因子。实际应用中,为了保证曲线不出现渐近线,通常取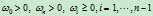 。
。
定义6.2
在射影空间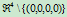 中给定
中给定 个点
个点
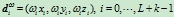
并给定一节点矢量 ,则一条参数
,则一条参数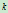 次NURBS曲线定义为如下的参数分段
次NURBS曲线定义为如下的参数分段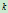 次有理多项式矢值函数:
次有理多项式矢值函数:
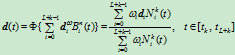 (6.1.4)
(6.1.4)
其中 称为曲线
称为曲线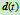 的de Boor点,
的de Boor点,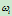 亦称为权因子。
亦称为权因子。
6.1.2 参数有理曲线的性质
参数有理多项式曲线除了具有参数多项式曲线的全部性质之外,还具有以下重要的性质:
- 当
 时,参数有理多项式曲线即为参数多项式曲线;
时,参数有理多项式曲线即为参数多项式曲线;
- 能够精确表示初等二次曲线(圆锥曲线);
- 权因子的引入增加了曲线设计的灵活性。权因子不是一数值而是几何量—四点的交比,它是射影不变量,因而在控制多边形不变的情况下,借助于图形输入设备可以以几何的方式进行交互修改;
- 参数有理多项式具有射影不变性。例如,参数有理多项式的透视投影还是参数有理多项式,这一点对于图形显示来说非常重要。要观察一个形体的透视图时,只需对定义它的控制顶点进行相应的透视变换,并适当地修改权因子,然后在观察平面上计算其点即可,这大大减少了计算量,提高了显示速度。
- 参数有理多项式方法能直接嵌入到已有的非有理设计程序之中,需要增加的存储和计算要求最少。
6.2 权因子的几何意义
权因子
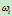 是四点
是四点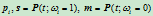 和
和 的交比,即
的交比,即
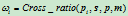
交比是射影不变量。由射影几何,共线四点
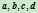 的交比定义为:
的交比定义为:
 (6.2.1)
(6.2.1)
它等于点
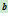 分
分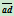 成两段的长度之比与点
成两段的长度之比与点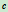 分
分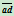 成两段的长度比的比值,这里的线段均为有向线段,因此线段长度为代数长度。我们知道,直线段被分成两子段的长度比在仿射变换下保持不变,然而在射影变换下就不再保持不变,但却保持上述的交比不变。如图6.1,有
成两段的长度比的比值,这里的线段均为有向线段,因此线段长度为代数长度。我们知道,直线段被分成两子段的长度比在仿射变换下保持不变,然而在射影变换下就不再保持不变,但却保持上述的交比不变。如图6.1,有
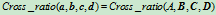 (6.2.2)
(6.2.2)
这称之为交比定理。
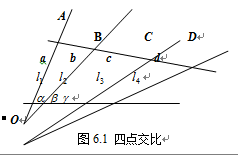
因为
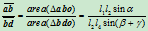
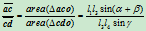
所以
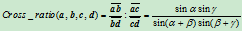 (6.2.3)
(6.2.3)
可见,共线四点
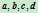 的交比仅与在投影中心
的交比仅与在投影中心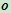 的角度有关,从
的角度有关,从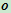 发出的四条射线可与任一直线相交,所得四个交点将有相同的交比,不管该直线怎样选择。
发出的四条射线可与任一直线相交,所得四个交点将有相同的交比,不管该直线怎样选择。
下面我们证明权因子确实为交比。令
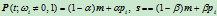
那么,由式(6.1.3)可知
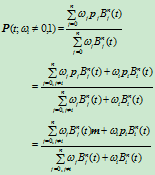
所以
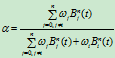
同理
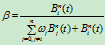
于是
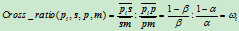 (6.2.4)
(6.2.4)
由此可以看出,权因子
 明确的几何意义:权因子
明确的几何意义:权因子 等于过控制顶点
等于过控制顶点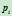 的一条直线上分别具有权因子
的一条直线上分别具有权因子 ,
,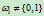 和0的那四个点
和0的那四个点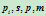 的交比。
的交比。
弄清了权因子
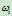 的几何意义之后,就可以容易地分析权因子对曲线形状的影响:
的几何意义之后,就可以容易地分析权因子对曲线形状的影响:
- 若固定所有控制顶点,除
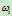 外的所有其他权因子保持不变,那么当
外的所有其他权因子保持不变,那么当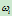 变化时,点
变化时,点 随之移动,它在空间扫出一条过控制顶点
随之移动,它在空间扫出一条过控制顶点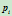 的直线。当
的直线。当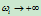 时,
时,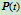 趋于
趋于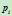 ;当
;当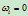 时,
时,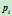 对曲线不产生任何影响。
对曲线不产生任何影响。
- 若
 增大,则
增大,则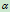 随之增大,曲线
随之增大,曲线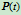 被拉向控制顶点
被拉向控制顶点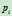 ;若
;若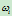 减小,则
减小,则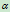 随之减小,曲线
随之减小,曲线 被推离控制顶点
被推离控制顶点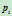 ,即权因子
,即权因子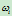 的减小与增大起到了对曲线
的减小与增大起到了对曲线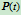 相对于控制顶点
相对于控制顶点 的推拉作用。
的推拉作用。
6.3 二次曲线的NURBS表示
6.3.1 二次曲线的隐式方程
二次曲线又称为圆锥截线,为平面曲线,其一般方程为
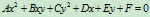
它含有六个系数,但只有五个是独立的。也就是说,一条二次曲线由五个独立的条件确定,然而这些系数的几何意义不明确。对实际工程应用来说,直接采用这种隐式方程显然是不方便的。因此,需要寻求有明显几何意义的、适合工程应用的条件和表示形式。
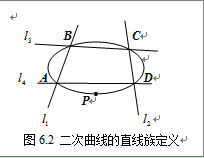
既然二次曲线的隐式方程中含有五个独立的自由量,那么最简单的条件是给定平面上五个独立的点来确定一条二次曲线。由于任意给定的五个点不一定能确定一条二次曲线(比如五点共线),因而通常用直线族首先定义一二次曲线族,然后再指定一点以确定惟一的一条二次曲线。
给定直线:

那么这四条直线便定义了一二次曲线族:
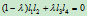 (6.3.1)
(6.3.1)
 它通过直线对
它通过直线对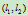 与直线对
与直线对 的四个交点
的四个交点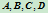 ,再给定第五个点
,再给定第五个点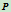 ,就可确定出族参数
,就可确定出族参数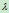 的值,从而确定了一条二次曲线(图6.2)。
的值,从而确定了一条二次曲线(图6.2)。


 如果点
如果点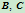 分别趋于点
分别趋于点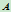 与
与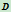 ,那么弦线
,那么弦线 与
与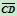 分别就成为曲线在
分别就成为曲线在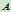 与
与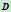 两点的切线。因此,若直线
两点的切线。因此,若直线 与
与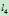 重合,则方程
重合,则方程
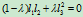 (6.3.2)
(6.3.2)
表示一族过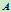 与
与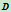 两点。且在
两点。且在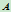 与
与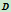 处的切线分别为
处的切线分别为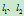 的二次曲线。若两切线不平行,则有交点
的二次曲线。若两切线不平行,则有交点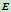 ,再给定曲线上另一点
,再给定曲线上另一点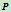 就可确定参数与
就可确定参数与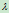 。
。
如果点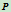 落在三角形
落在三角形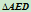 内,则二次曲线在三角形
内,则二次曲线在三角形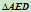 内总是一段连续的曲线弧,那么两端点
内总是一段连续的曲线弧,那么两端点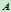 、
、 及其切线的交点
及其切线的交点 ,加上曲线上的位于三角形
,加上曲线上的位于三角形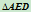 内的一点
内的一点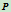 ,便是工程上定义一段二次曲线弧的五个独立条件(图6.3)。现在的问题是怎样找出它的NURBS表示?
,便是工程上定义一段二次曲线弧的五个独立条件(图6.3)。现在的问题是怎样找出它的NURBS表示?
6.3.2 二次曲线的有理Bézier表示
给定平面上不共线的三个点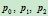 ,则以过
,则以过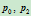 ,在
,在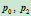 处分别与
处分别与 、
、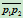 相切为条件,可定义一二次曲线族。若记
相切为条件,可定义一二次曲线族。若记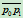 、
、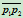 、
、 的方程分别为
的方程分别为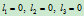 ,则二次曲线族的方程为
,则二次曲线族的方程为
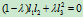
现以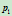 为原点,
为原点,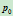 为
为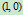 点,
点, 为
为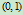 点建立平面斜坐标系
点建立平面斜坐标系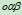 。在该坐标系下,平面上任一点
。在该坐标系下,平面上任一点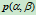 可表示为
可表示为
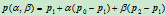
直线 、
、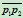 、
、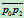 的方程分别为
的方程分别为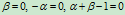 。因此,二次曲线族的方程为
。因此,二次曲线族的方程为
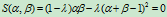
这里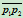 的方程取为
的方程取为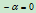 ,而不是
,而不是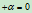 ,其原因是当确定二次曲线的第五个点位于三角形
,其原因是当确定二次曲线的第五个点位于三角形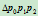 内时,对应的族参数
内时,对应的族参数 。
。
设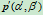 是二次曲线上任一点,那么曲线在该点处的切线分别交
是二次曲线上任一点,那么曲线在该点处的切线分别交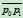 、
、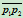 与
与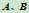 。当
。当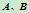 沿直线
沿直线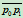 、
、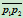 变动时,
变动时, 则沿曲线变动。因此,比率
则沿曲线变动。因此,比率

可看作是点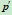 处的参数。
处的参数。
由方程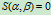 可求出曲线在
可求出曲线在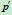 的切线与
的切线与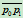 和
和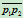 交点
交点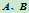 的坐标。点
的坐标。点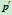 的切线方程为
的切线方程为
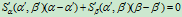
其中,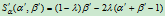 ,
, 。
。
交点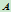 的坐标为
的坐标为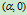 ,将
,将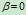 代入上式,有
代入上式,有
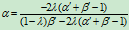
所以
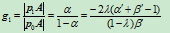
同理
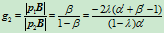
因此
 (6.3.2)
(6.3.2)
这表明,对任一二次曲线, 是常量,且当第五点位于三角形
是常量,且当第五点位于三角形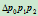 内时,
内时,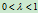 。
。
此时,点 可以按参数
可以按参数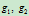 表示。由
表示。由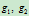 的表示式可知:
的表示式可知:
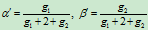
再由的表达式,便有
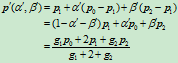
现令

代入上式,便有

这便是一有理二次Bézier曲线,且
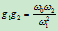 (6.3.3)
(6.3.3)
上述讨论表明,任一二次曲线都可以表示成有理二次Bézier曲线。反之,有理二次Bézier曲线又是什么呢?
设
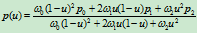
是一理二次Bézier曲线,那么按照重心坐标形式可将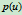 改写如下:
改写如下:
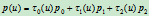
由中心坐标的定义,有
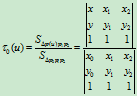 ,
,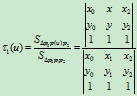 ,
,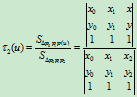
另一方面,由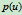 的表达式可知:
的表达式可知:
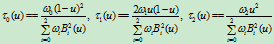
消去参数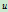 ,则有
,则有
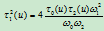
这表明, 的隐式方程是
的隐式方程是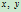 的二次方程,即
的二次方程,即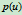 为二次曲线。因而圆锥曲线与理二次Bézier曲线等价。
为二次曲线。因而圆锥曲线与理二次Bézier曲线等价。
6.3.3 有理二次Bézier曲线的形状分类
给定有理二次Bézier曲线之后,既然它就是圆锥曲线,那么我们要问当权因子满足什么条件时,给定的有理二次Bézier曲线分别是抛物线、双曲线和椭圆,这就是有理二次Bézier曲线的形状分类。
在回答这个问题之前,我们先讨论圆锥曲线的补弧。设
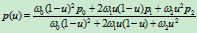
为一圆锥曲线,其中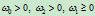 。那么曲线
。那么曲线
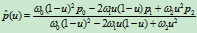
也是一条由相同控制顶点定义的二次曲线。由于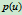 与
与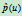 具有相同的隐式方程,所以它们同属于一条二次曲线。显然,对给定的参数
具有相同的隐式方程,所以它们同属于一条二次曲线。显然,对给定的参数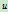 ,点
,点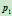 ,
,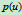 和
和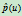 共线,因而,
共线,因而,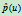 的行为便决定了二次曲线的类型。当
的行为便决定了二次曲线的类型。当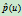 在
在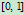 内无奇点时,二次曲线为椭圆;如果
内无奇点时,二次曲线为椭圆;如果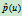 在
在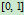 内有一个奇点,则二次曲线是抛物线;而当有两个奇点时,二次曲线是双曲线。
内有一个奇点,则二次曲线是抛物线;而当有两个奇点时,二次曲线是双曲线。
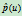 的奇点就是
的奇点就是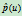 的无限远点,它由
的无限远点,它由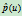 在
在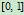 内的分母在
内的分母在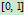 内的根所决定。它在
内的根所决定。它在 内的根最多有两个,其表达式为
内的根最多有两个,其表达式为

因此,有理二次Bézier曲线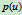 的形状分类如下:
的形状分类如下:
 (6.3.4)
(6.3.4)
特别,当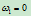 时,
时,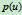 为连接
为连接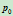 与
与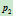 的直线段;当
的直线段;当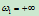 时,
时,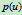 则退化为直线对
则退化为直线对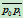 和
和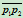
6.3.4 圆的NURBS表示
圆弧是非常特殊的圆锥曲线,也是工程设计中最常用的曲线之一,如曲线间的圆角过渡、倒圆角等都用到圆弧。所以,有必要对圆弧的NURBS表示问题作以专门讨论。
给定有理二次Bézier曲线
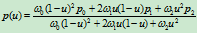
由于 在
在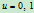 处分别相切于边
处分别相切于边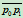 和
和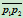 ,所以
,所以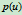 为圆弧的必要条件是
为圆弧的必要条件是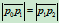 ,其原因是由圆外一点向圆做的两条切线长度相等。我们的目的是寻找充分必要条件,对此有以下结论:
,其原因是由圆外一点向圆做的两条切线长度相等。我们的目的是寻找充分必要条件,对此有以下结论:
一条有理二次Bézier曲线为圆弧的充要条件是
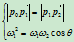 (6.3.4)
(6.3.4)
其中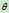 为向量
为向量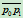 和
和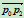 之间的夹角(图6.4)。设
之间的夹角(图6.4)。设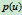 为一圆弧,则其圆心为
为一圆弧,则其圆心为
 (6.3.5)
(6.3.5)
基于圆的有理二次Bézier表示条件,便可给出各种圆弧的NURBS表示。

- 四分之一圆弧:
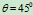
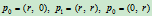
取
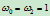 ,则
,则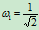 。
。
- 三分之一圆弧:
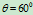
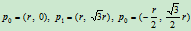
取
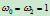 ,则
,则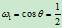
- 半圆:
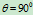
令
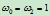 ,则
,则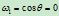 。由于此时两切线的交点
。由于此时两切线的交点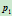 在无穷远处,按照齐次坐标与非齐次坐标之间的对应关系,齐次分量为零的点表示非齐次空间一矢量。控制顶点
在无穷远处,按照齐次坐标与非齐次坐标之间的对应关系,齐次分量为零的点表示非齐次空间一矢量。控制顶点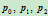 的齐次坐标分别为:
的齐次坐标分别为:
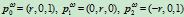
所以,半圆的齐次表示是:
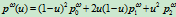
相应的非齐次表示如下:
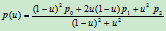 (6.3.6)
(6.3.6)
当然,可以通过插入节点的方式消去无限远点
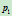 。例如,半圆弧插入节点后可表示为入下的二次NURBS曲线:
。例如,半圆弧插入节点后可表示为入下的二次NURBS曲线:
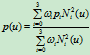 (6.3.7)
(6.3.7)
其中,
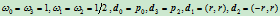 ,
,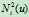 由节点矢量
由节点矢量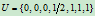 所确定。
所确定。
- 圆心角大于
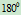 的圆弧的表示问题
的圆弧的表示问题
对于这种情况,若用一段有理二次Bézier曲线段表示之,那么由条件
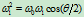 可知,权因子
可知,权因子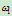 为负值,不符合有理曲线定义中关于权因子非负的约定。因而需将圆弧分割成若干段,使其每一段的圆心角均小于
为负值,不符合有理曲线定义中关于权因子非负的约定。因而需将圆弧分割成若干段,使其每一段的圆心角均小于 ,然后求得每一段的有理二次Bézier表示,最后再合并成NURBS表示形式。
,然后求得每一段的有理二次Bézier表示,最后再合并成NURBS表示形式。
- 整圆的NURBS表示
由于整圆的圆心角为
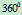 ,所以按照4.之讨论,需将整圆分割成几段才能获得要求的NURBS表示。
,所以按照4.之讨论,需将整圆分割成几段才能获得要求的NURBS表示。
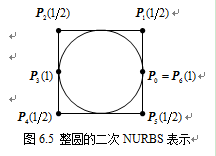
10 四段构成的圆
此时的控制顶点及权因子如图6.5所示。二次B样条基函数
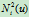 由下列节点矢量所确定:
由下列节点矢量所确定:

曲线的表示式为:
20 三段构成的圆
此时的控制顶点及权因子如图6.6所示。二次B样条基函数
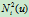 由下列节点矢量所确定:
由下列节点矢量所确定:
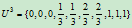
曲线的表示式为:
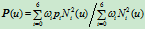
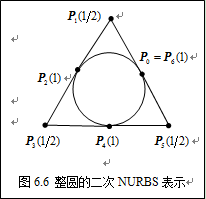
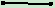
 整圆的这两种表示方式非常有趣,重节点
整圆的这两种表示方式非常有趣,重节点 的使用意味着基函数仅为
的使用意味着基函数仅为 连续,但曲线却处处
连续,但曲线却处处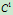 连续非
连续非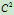 连续,仅为
连续,仅为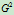 连续,其原因何在呢?实际上,作为它们对应的齐次坐标表示的高一维空间的参数多项式曲线,即确为
连续,其原因何在呢?实际上,作为它们对应的齐次坐标表示的高一维空间的参数多项式曲线,即确为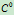 连续。这表明射影变换改变了曲线的特性,因为连续性不是射影不变量。这给我们提出了一个问题:有理曲线的连续性与它的齐次坐标曲线的连续性之间有什么联系?如何借助于齐次曲线度量有理曲线的连续性?
连续。这表明射影变换改变了曲线的特性,因为连续性不是射影不变量。这给我们提出了一个问题:有理曲线的连续性与它的齐次坐标曲线的连续性之间有什么联系?如何借助于齐次曲线度量有理曲线的连续性?

 由上面的讨论可以看出,要想用有理二次曲线段表示一整圆最少需要二段,即两个半圆。如果不采用无限远点,
那么用有理二次曲线表示整圆至少需要六个控制顶点,其节点矢量中最少有一个二重节点。
由上面的讨论可以看出,要想用有理二次曲线段表示一整圆最少需要二段,即两个半圆。如果不采用无限远点,
那么用有理二次曲线表示整圆至少需要六个控制顶点,其节点矢量中最少有一个二重节点。
当然,另外一种表示整圆的方法是采用补弧。设

为一圆弧,那么曲线
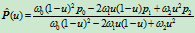
则为整圆除
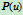 段外的剩余部分。这里采用了小于零的权因子,一般很少在CAD/CAM中采用。
段外的剩余部分。这里采用了小于零的权因子,一般很少在CAD/CAM中采用。
6.3.5 有理Bézier曲线的参数变换
我们早已知道,同一条参数曲线的表示式不惟一,可以通过正则参数变换
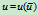 ,
,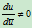 将曲线重新参数化。由老参数表示的
将曲线重新参数化。由老参数表示的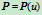 改变为新参数表示的
改变为新参数表示的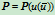 ,这一参数变换不改变曲线的形状,但改变了参数化,即曲线上点与参数域内点的对应关系的形状。
,这一参数变换不改变曲线的形状,但改变了参数化,即曲线上点与参数域内点的对应关系的形状。
那么,对有理Bézier曲线应进行怎样的参数变换以改变曲线的参数化,同时又保持曲线的次数及定义域不变呢?这种参数变换对权因子产生怎样的影响呢?下面就这些问题进行讨论。
- 有理线性变换
由于四共线点的交比在射影变换下不变,通过交比可在两条直线间建立起射影变换关系,它刊物用有理分式表示。因而,有理线性变换可用于有理Bézier曲线的重新参数化。
令
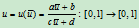 为要求的有理线性变换,那么根据条件
为要求的有理线性变换,那么根据条件 可得
可得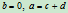 ,从而有
,从而有
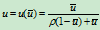
其中
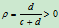 为任意常数。
为任意常数。
对于给定的有理
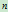 次Bézier曲线
次Bézier曲线


做上述参数变换,对其重新参数化后,有
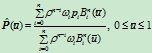
这等价于给出了一组特殊的新权因子:




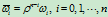
由
 和
和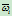 所定义的曲线
所定义的曲线
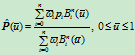
与曲线
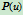 完全相同,唯一的区别在于曲线上点的分布。
完全相同,唯一的区别在于曲线上点的分布。
既然对有理Bézier曲线进行参数变换等价于重新选择权因子,那么我们要问:有理Bézier曲线中独立的权因子的个数有多少?
- 有理
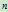 次Bézier曲线中独立权因子的个数
次Bézier曲线中独立权因子的个数
若令
 ,对
,对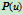 做参数变换
做参数变换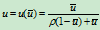 ,则有
,则有
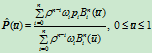
此时,新权因子满足条件:
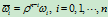
特别,
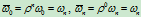 。
。
对曲线
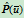 的分子分母同除以
的分子分母同除以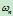 ,便得到新的权因子
,便得到新的权因子

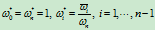
由此可见,对任意给定的
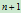 个权因子,我们总可以对相应的曲线进行重新参数化,使其首末两个权因子为1,因而对立权因子的个数只有
个权因子,我们总可以对相应的曲线进行重新参数化,使其首末两个权因子为1,因而对立权因子的个数只有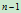 个。
个。
为了区分起见,我们称首末权因子为1的有理
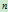 次Bézier曲线
次Bézier曲线
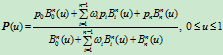
为标准型有理
 次Bézier曲线。
次Bézier曲线。
有理线性变换表明,所有非标准型有理
 次Bézier曲线都可以转换成标准型。
次Bézier曲线都可以转换成标准型。
6.3.6 有理二次Bézier曲线的确定
根据前面的讨论可知,有理二次Bézier曲线就是初等二次曲线。一条初等二次曲线由五个独立的条件所确定,通常确定一条二次曲线的方法是基于Pascal定理。
【Pascal定理】给定圆锥曲线上六个互不相同且任意三个均不共线的点,如图6.7 所示,构造六条直线,则交点
 共线。
共线。
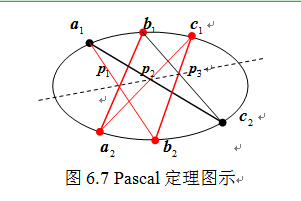
给定五个互不相同且任意三个均不共线的点
 ,可按Pascal定理构造出由其确定的二次曲线上任一点
,可按Pascal定理构造出由其确定的二次曲线上任一点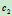 。构造过程如下:连接
。构造过程如下:连接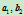 ,
,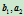 ,
,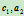 ,
, ,求
,求 与
与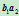 的交点
的交点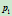 。给定过
。给定过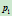 的任一直线
的任一直线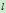 ,求
,求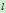 与
与 ,
,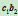 的交点那么
的交点那么 ,那么直线
,那么直线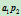 与
与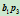 之交点即为二次曲线上的点
之交点即为二次曲线上的点 。当
。当 绕
绕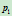 旋转时,点
旋转时,点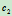 便扫出要求的二次曲线。
便扫出要求的二次曲线。
下面我们以有理二次Bézier曲线的标准型为例,讨论有理二次Bézier曲线的确定问题。
- 给定曲线上三点
 及
及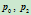 处的切线,求其确定的二次曲线
处的切线,求其确定的二次曲线
设
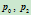 处切线的交点为
处切线的交点为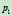 ,那么由此确定的二次曲线具有以下有理参数表示:
,那么由此确定的二次曲线具有以下有理参数表示:
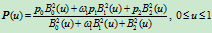
方法1:求点
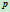 关于三角形
关于三角形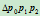 的重心坐标。设
的重心坐标。设
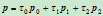
那么,由上式可知
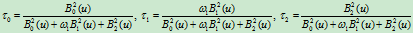
消去参数
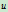 ,则于
,则于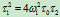 ,即
,即
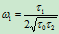
方法2:过
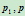 做直线交边
做直线交边 于点
于点 ,可求得点
,可求得点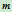 分边
分边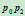 为两段的比值
为两段的比值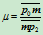 。因点
。因点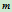 与
与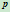 具有相同的参数
具有相同的参数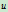 ,由此点
,由此点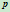 的参数为
的参数为
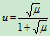
由所求参数
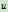 ,按非有理de Castljau算法求出
,按非有理de Castljau算法求出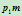 上一点
上一点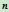 ,此时直线
,此时直线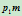 上四点
上四点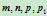 所在的有理二次Bézier曲线分别具有内权因子
所在的有理二次Bézier曲线分别具有内权因子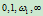 。根据权因子的几何意义,可知
。根据权因子的几何意义,可知
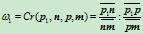
- 给定曲线上两点
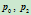 ,
,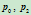 处的切线,及曲线的另一条切线,求其确定的二次曲线
处的切线,及曲线的另一条切线,求其确定的二次曲线
设
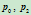 处切线的交点为
处切线的交点为 ,那么由此确定的二次曲线具有以下的有理参数表示:
,那么由此确定的二次曲线具有以下的有理参数表示:
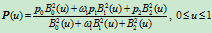
设另一条切线与
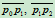 之交点分别为
之交点分别为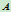 和
和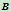 ,记
,记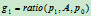 ,
,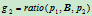 。由于
。由于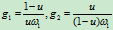 。因此
。因此
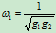
下面,我们作为本章的结束,考察一个例子。给定不共线的三个控制顶点
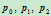 及两组非零权因子
及两组非零权因子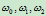 与
与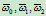 满足条件
满足条件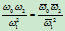 ,求证:
,求证:
① 这两组权因子定义同一条二次曲线;
② 求曲线从权因子
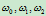 变换为权因子
变换为权因子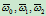 时相应的参数变换。
时相应的参数变换。
证明 设
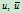 分别表示曲线上同一点相应权因子
分别表示曲线上同一点相应权因子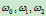 与
与 之参数,那么由有理曲线的参数变换可知:
之参数,那么由有理曲线的参数变换可知:
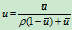
我们只需确定出参数
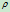 即可。为此,考察曲线上离弦
即可。为此,考察曲线上离弦 距离最大的点
距离最大的点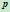 。该点处之切线必平行于弦线,于是
。该点处之切线必平行于弦线,于是 。因而点
。因而点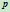 为
为 ,
,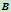 之中点。
之中点。
由于
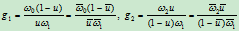
所以点
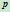 对应的参数分别为
对应的参数分别为
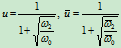
代入参数变换公式,有
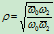
- 三分之一圆弧:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号