参数估计就是要从样本出发构造一些统计量作为总体某些参数(或数字特征)的估计量。
点估计就是构造统计量。
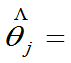
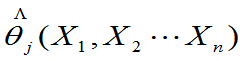 j=1,2,…n
j=1,2,…n
以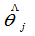 的值作为
的值作为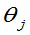 的近似值。对
的近似值。对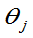 进行估计,叫(点)估计量。若样本值代入
进行估计,叫(点)估计量。若样本值代入 称为
称为 的估计值。
的估计值。
区间估计是根据样本构造出适当的区间,它以一定的概率包含未知参数。
§7.1 点估计
(一)矩估计法
1.矩估计法的基本思想
在总体的各阶矩存在的条件下,用样本的各阶矩去估计总体相应的各阶矩,又由于总体的分布类型已知,总体的各阶矩可表示为未知参数的已知函数,这样样本的各阶矩就与未知参数的已知函数联系起来,从而得到参数的各阶矩。
2.一般求法
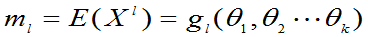
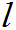
 =1,2…k
=1,2…k
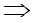
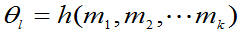
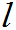 =1,2…k
=1,2…k
令 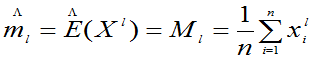
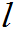 =1,2…k
=1,2…k
将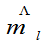 代入中,
代入中,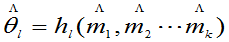
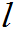 =1,2…k
=1,2…k
例 2 P159总体X~U[a,b],参数a,b未知,求a,b的矩估计。
例 3 P160
以下为第一版例。
例7:总体X~U[0,b],参数b未知,求b的矩估计。
例8:总体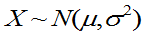 ,
,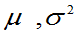 未知,已知
未知,已知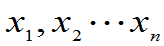 是来自总体X的样本值,求
是来自总体X的样本值,求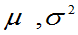 的矩估计。
的矩估计。
例9:总体的概率密度为

参数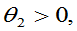
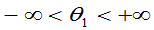 均未知,
均未知,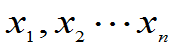 是来自总体的样本,求
是来自总体的样本,求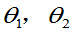 的矩估计。
的矩估计。
3.总体的数学期望与方差的矩估计
已知总体的二阶矩存在, 是来自总体的样本值。E(X),D(X)的矩估计是
是来自总体的样本值。E(X),D(X)的矩估计是

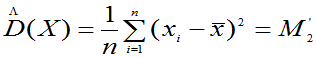
注意: 此结论用于只要E(x)、D(x)存在的,不论分布是否已知的各类型总体的数字特征E(X)、D(X)的矩估计。
例:总体X~B(N,p), 参数N、0<p<1均未知,已知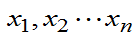 是来自总体的样本值,求N,p的矩估计 。
是来自总体的样本值,求N,p的矩估计 。
(二) 最大似然估计法
- 最大似然估计法的基本思想
例:设在一个口袋中装有许多白球和黑球,但不知是黑球多还是白球多,只知道两种球的数量之比为1:3就是说抽取到黑球的概率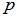 为
为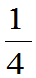 或
或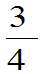 。
。
如果用有放回抽取的方法从口袋中抽取n=3个球,发现有一个是黑球,试判断p=?。
X | 0 | 1 | 2 | 3 |
|
|
|
|
|
|
|
|
|
|
当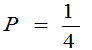 时,P(取的三个球中有一个黑球)=
时,P(取的三个球中有一个黑球)= 大。选取参数
大。选取参数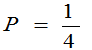 总体较合理。故取p的估计值
总体较合理。故取p的估计值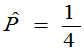 。
。
最大似然估计基本思想:根据样本的具体情况,选择参数p的估计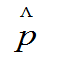 ,使得该样本发生的概率最大。
,使得该样本发生的概率最大。
2.最大似然估计的求法
设总体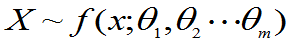 的形式已知,参数
的形式已知,参数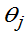 未知(j=1,2…m),
未知(j=1,2…m),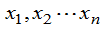 是来自总体的样本值。
是来自总体的样本值。
记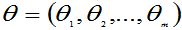 ,选择参数的估计
,选择参数的估计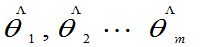 ,使样本
,使样本 取值
取值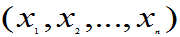 附近的概率
附近的概率
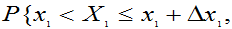
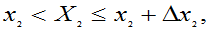 …
…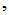
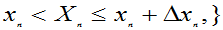
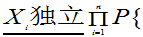
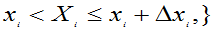 =
=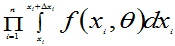
=
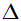
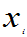 达到最大,
达到最大,
等价使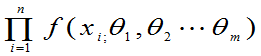 达到最大。
达到最大。
称L=L( )=
)=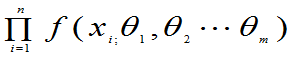 为样本值
为样本值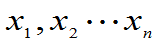 的似然函数。
的似然函数。
定义7.1如果似然函数L=L(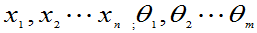 )在
)在 达到最大值,则称
达到最大值,则称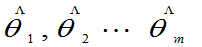 分别为
分别为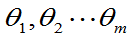 的最大似然估计。
的最大似然估计。
2.一般步骤
(1).当似然函数可微且参数集合是开集的条件下:
- 总体
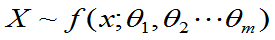 ,
,
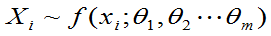 i =1,2…n
i =1,2…n
L=L(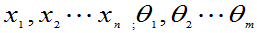 )=
)=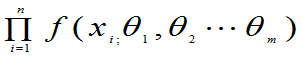
取对数 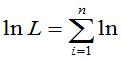
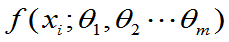
②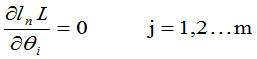
③由似然方程解出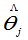 =?.。讨论
=?.。讨论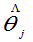 是最大值点,则它是
是最大值点,则它是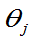 的最大似然估计。
的最大似然估计。
例4 P162 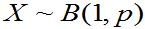 ,求未知参数
,求未知参数  的最大似然估计。
的最大似然估计。
例 5 P163 总体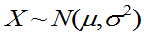 ,
,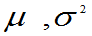 未知, 已知
未知, 已知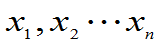 是来自总体X的样本值,求
是来自总体X的样本值,求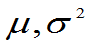 的最大似然估计。
的最大似然估计。
例 6 P165 总体X~U[a,b],参数a,b未知, 已知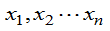 是来自总体的样本值,求b的最大似然估计。
是来自总体的样本值,求b的最大似然估计。
以下为第一版例。
例2:总体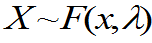 =
=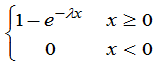
参数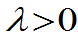 未知,
未知,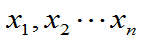 是来自总体的样本值,求
是来自总体的样本值,求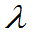 的最大似然估计。
的最大似然估计。
例3: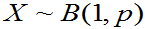 ,求未知参数
,求未知参数 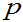 的最大似然估计。[见书P159,例7.1]
的最大似然估计。[见书P159,例7.1]
总体X是离散值,一定要写出X的概率函数。
例4:一个罐子里装有黑球和白球,每次从中随机的有放回地抽取一个球,直到抽到黑球为止。设停止抽球时所需抽取数是X,这样独立重复的进行了n次实验,获得样本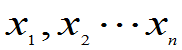 ,试求罐子里黑球所占的比例中的最大似然估计。
,试求罐子里黑球所占的比例中的最大似然估计。
例5:X服从参数为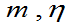 的威布尔分布,而
的威布尔分布,而
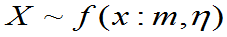 =
=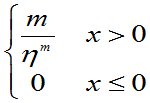
m>0,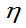 >0且
>0且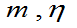 未知,
未知,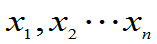 是来自总体的样本值,求参数的最大似然估计。
是来自总体的样本值,求参数的最大似然估计。
(2)当似然函数L不可数时,或似然函数无解,要用定义求参数的最大似然估计。
例6:总体X~U[0,b],参数b未知, 已知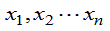 是来自总体的样本值,求b的最大似然估计。
是来自总体的样本值,求b的最大似然估计。
3.未知参数的已知函数的最大似然估计有如下规定:
若 ,未知参数的已知函数为
,未知参数的已知函数为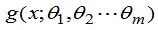 ,
,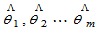 分别为
分别为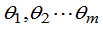 的最大似然估计,则规定g(
的最大似然估计,则规定g(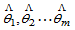 )为g(
)为g(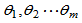 )的最大似然估计。
)的最大似然估计。
例:P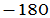 习题7.5。
习题7.5。
§7.2 估计量评选标准
1.无偏性:
定义:设 (
(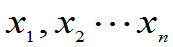 )是
)是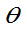 的估计量,若E(
的估计量,若E(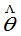 )=
)=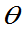 ,对一切
,对一切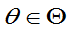 ,则称
,则称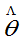 为
为 的无偏估计量,否则称为
的无偏估计量,否则称为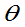 的有偏估计量。其偏差度为
的有偏估计量。其偏差度为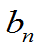 = E(
= E(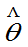 )-
)- 。如果
。如果 E(
E(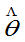 )=
)= ,则称
,则称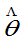 为
为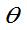 的渐近无偏估计量。
的渐近无偏估计量。
书上定义是对g(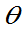 )而言的:
)而言的:
定义:设未知参数的已知函数g(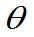 )的估计量为
)的估计量为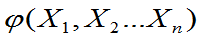 ,如果对一切
,如果对一切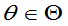 都有
都有
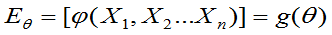
则称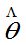 为
为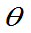 的无偏估计量。
的无偏估计量。
例10:设总体有二阶矩,E(X)=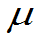 ,D(X)=
,D(X)=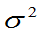 存在,
存在,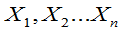 是该总体的样本,证明
是该总体的样本,证明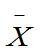 为
为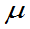 的无偏估计,
的无偏估计,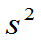 为
为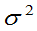 的无偏估计,但
的无偏估计,但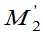 不是
不是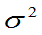 的无偏估计,是
的无偏估计,是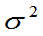 的渐近无偏估计。
的渐近无偏估计。
例11:总体X~U[a,b],b>0,试问b的矩估计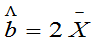 是否是b的无偏估计量。
是否是b的无偏估计量。

注意:
(1)若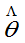 为
为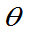 的无偏估计,g(
的无偏估计,g(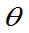 )为
)为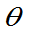 的已知函数,而g(
的已知函数,而g(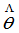 )不一定是g(
)不一定是g( )的无偏估计。
)的无偏估计。
(2)有时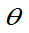 的有偏估计也可稍加修改为无偏估计。
的有偏估计也可稍加修改为无偏估计。
例:设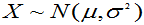 ,
,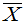 是
是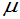 的无偏估计,但
的无偏估计,但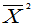 不是
不是
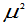 的无偏估计,可修改为
的无偏估计,可修改为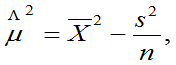 它是
它是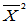 的无偏估计。
的无偏估计。
2.有效性
定义:若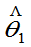 和
和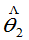 都为
都为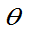 的无偏估计量。若
的无偏估计量。若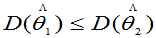 ,
,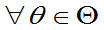 且至少对一个
且至少对一个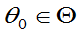 ,有严格不等号成立,则称
,有严格不等号成立,则称 比
比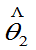 有效。
有效。
例12:比较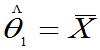 ,
, ,(
,(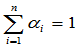 )。估计
)。估计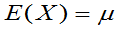 ,哪个有效。
,哪个有效。
定义:设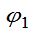
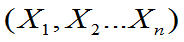 和
和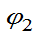
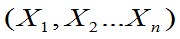 都是g(
都是g( )的估计量, 如果对一切
)的估计量, 如果对一切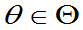 都有
都有
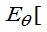
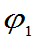
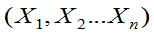 -g(
-g( )]
)]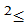
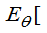
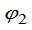
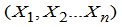 - g(
- g(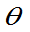 )]
)]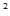
且存在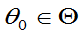 ,有严格不等号成立,则称
,有严格不等号成立,则称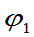 比
比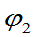 有效。
有效。
此定义为均方误差准则。
3.相合性(一致估计量)
定义7.5:设g(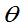 )的估计量为
)的估计量为 ,如果对任意的
,如果对任意的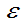 >0,都有
>0,都有

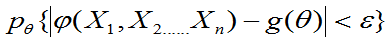 =1
=1
则称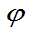 为
为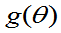 的相合估计量。
的相合估计量。
§7.2 区间估计
一.基本概念
设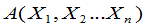 ,
, 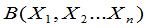 是两个统计量,且满足
是两个统计量,且满足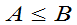 ,则称[A,B]为一随机区间。
,则称[A,B]为一随机区间。
定义7.6:对于给定的正数 ,如果对一切
,如果对一切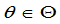 都有
都有
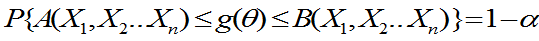
则称[A,B]为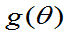 的置信度为
的置信度为 的置信区间,称
的置信区间,称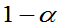 为置信区间的置信度,称A、B分别为置信下限和置信上限。
为置信区间的置信度,称A、B分别为置信下限和置信上限。
常用的形式:

例:某旅游社为调查当地每一旅游者的平均消费额,随机访问了100名旅游者,得知平均消费额 (元)。根据经验,已知旅游者消费额服从正态分布
(元)。根据经验,已知旅游者消费额服从正态分布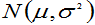 ,且标准差
,且标准差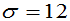 (元),那麽该地旅游者平均消费额
(元),那麽该地旅游者平均消费额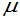 的置信度为95%的置信区间是什麽。
的置信度为95%的置信区间是什麽。
设旅游者消费额为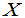 ,且知
,且知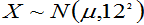 ,此题是求
,此题是求
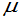 的置信区间的问题。
的置信区间的问题。
(1)找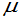 的较好点估计(最大似然估计或无偏估计),
的较好点估计(最大似然估计或无偏估计),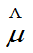
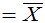 。
。
(2)为使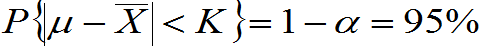 ,要选有关
,要选有关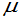 与
与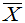 的函数且知其分布。当已知
的函数且知其分布。当已知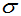 时,
时,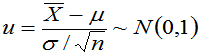 ,
,
称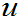 为枢轴变量。对给定的
为枢轴变量。对给定的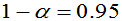 ,使
,使
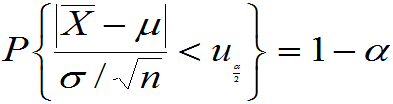
(3)将不等式 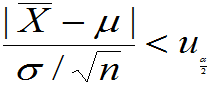
 等价变形
等价变形
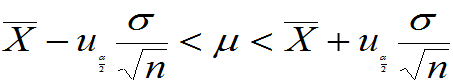
本例,计算 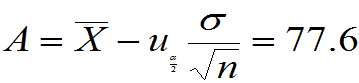
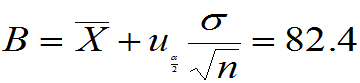
得到,当地每位旅游者置信度为95%的平均消费额在[77.6元,82.4元]之间。
Data;
u=probit(1-0.05/2);put u=;
A=80-(u*12)/sqrt(100); put A=;
B=80+(u*12)/sqrt(100); put B=;
run;
u=1.9599639845
A=77.648043219
B=82.351956781
定义: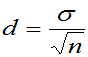 叫区间半径,
叫区间半径,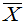 叫区间中心,
叫区间中心,
 叫区间长度。
叫区间长度。
二.置信区间的一般求法 (枢轴量法)
(1)从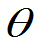 的一个较好点估计
的一个较好点估计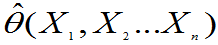 出发,构造
出发,构造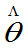 与
与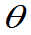 的一个函数
的一个函数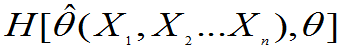 ,且知其分布又与
,且知其分布又与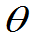 无关,函数H称为枢轴变量。
无关,函数H称为枢轴变量。
(2)记H的上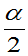 分为数和上(1-
分为数和上(1-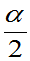 )分位数为
)分位数为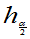 和
和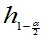 ,使对给定的
,使对给定的 ,有
,有

利用不等式运算,将不等式
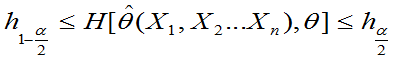 进行等价变形,使得最后得到形如:
进行等价变形,使得最后得到形如:

的不等式。
则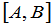 就是
就是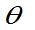 的
的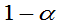 置信区间,这时有:
置信区间,这时有:
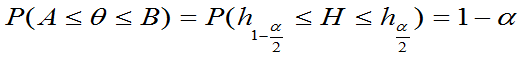
定义: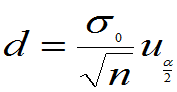 叫区间半径,
叫区间半径,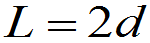 或
或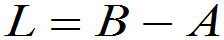 叫区间长度。
叫区间长度。
例1 P170,计算机实现过程。
Data;
z=probit(1-0.05/2);put z=;
A=5.2-(z*1)/sqrt(16); put A=;
B=5.2+(z*1)/sqrt(16); put B=;
C=B-A; put C=;
run;
z=1.9599639845
A=4.7100090039
B=5.6899909961
C=0.9799819923
P171页下面部分的数值解释。
Data;
u1=probit(0.04);put u1=;
u2=probit(1-0.01);put u2=;
A=5.2+(u1*1)/sqrt(16); put A=;
B=5.2+(u2*1)/sqrt(16); put B=;
C=B-A; put C=;
run;
u1=-1.750686071
u2=2.326347874
A=4.7623284822
B=5.7815869685
C=1.0192584863
三.正态总体的参数的区间估计
1.一个正态总体的均值、方差的置信区间
设总体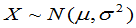 ,
, 是来自总体
是来自总体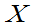 的样本
的样本
(1)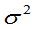 已知,均值
已知,均值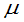 的置信度为
的置信度为 的置信区间为:
的置信区间为:
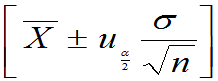
(2)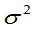 未知,均值
未知,均值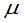 的置信度为
的置信度为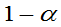 的置信区间为:
的置信区间为:
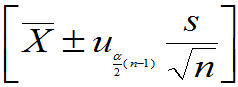 。
。
(3)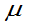 未知,方差
未知,方差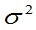 的置信度为
的置信度为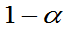 的置信区间为:
的置信区间为:
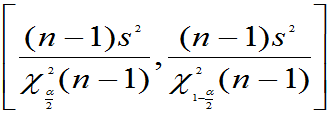
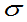 的
的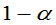 的置信区间为:
的置信区间为:
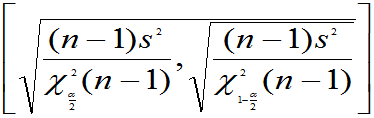
- 两个正态总体均值差方差比的置信区间
总体 | 样本 | 均值 | 样本方差 |
|
|
|
|
|
|
|
|
两个样本相互独立。
(1)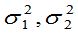 已知,均值差
已知,均值差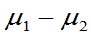 的置信区间为
的置信区间为
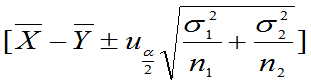
(2) 未知,但
未知,但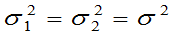 ,
,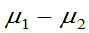 的置信区间为
的置信区间为
[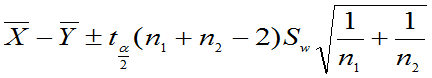 ]
]
(3)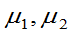 未知,方差比
未知,方差比 的置信区间为:
的置信区间为:
[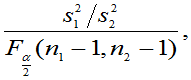
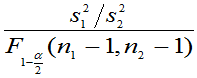 ]
]
(4) 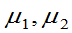 已知,
已知,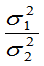 的置信区间为:
的置信区间为:
[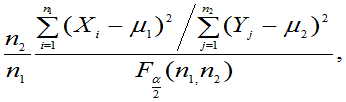
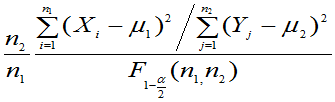 ]
]
- P174
Data;
t=TINV((1-0.05/2),15); put t=;
A=503.75-t*6.2022/sqrt(16); put A=;
B=503.75+t*6.2022/sqrt(16); put B=;
C=B-A; put C=;
run;
t=2.1314495456
A=500.44508091
B=507.05491909
C=6.6098381857
例2 P175
Data;
k1=CINV(1-0.05/2, 15);put k1=;
k2=CINV(0.05/2, 15);put k2=;
A=sqrt(15)*6.2022/sqrt(k1); put A=;
B= sqrt(15)*6.2022/sqrt(k2); put B=;
C=B-A; put C=;
run;
k1=27.488392863
k2=6.262137795
A=4.5815952687
B=9.5990905015
C=5.0174952328
例 3 P177
Data;
t=tINV(1-0.05/2, 28);put t=;
sw=sqrt((9*1.1**2+19*1.2**2)/28); put sw=;
A=500-496-sw*t*sqrt(1/10+1/20); put A=;
B=500-496+sw*t*sqrt(1/10+1/20); put B=;
C=B-A; put C=;
run;
t=2.0484071418
sw=1.1687905837
A=3.0727462146
B=4.9272537854
C=1.8545075707
例 4 P177
Data;
t=tINV(1-0.05/2, 14);put t=;
sw=sqrt((7*3.89+7*4.02)/14); put sw=;
A=91.73-93.75-sw*t*sqrt(1/8+1/8); put A=;
B=91.73-93.75+sw*t*sqrt(1/8+1/8); put B=;
C=B-A; put C=;
run;
t=2.1447866879
sw=1.9887181801
A=-4.152688139
B=0.1126881394
C=4.2653762788
例 5 P179
data ;
F1=FINV(1-0.1/2, 17,12) ; put F1=;
F2=FINV(0.1/2, 17,12) ; put F2=;
A=0.34/(0.29*F1); put A=;
B=0.34/(0.29*F2); put B=;
C=B-A; put C=;
Run;
F1=2.5828389059
F2=0.4200526125
A=0.4539244745
B=2.7911117756
C=2.3371873011
§7.5 (0---1)分布参数的区间估计
P179
例 P180
data;
z=probit(1-0.05/2);put z=;
a=100+z**2; put a=;
b=-(2*100*0.6+z**2); put b=;
c=100*0.6**2; put c=;
p1=1/(2*a)*(-b-sqrt(b**2-4*a*c)); put p1=;
p2=1/(2*a)*(-b+sqrt(b**2-4*a*c)); put p2=;
p=p2-p1; put p=;
run;
z=1.9599639845
a=103.84145882
b=-123.8414588
c=36
p1=0.5020025868
p2=0.6905987136
p=0.1885961268
§7.6 单侧置信区间
对于均值,单侧置信区间下限。公式(6.4)
对于方差,单侧置信区间上限。公式(6.6)
例 P182
Data;
t=tINV(1-0.05, 4);put t=;
mu=1160-sqrt(9950/5)*t; put mu=;
run;
t=2.1318467863
mu=1064.8995598
习题:
1,2,3,5,6,10,14,15,19,25


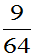
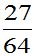
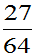
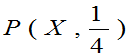

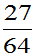

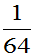
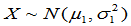
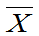

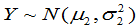

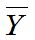
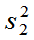


 浙公网安备 33010602011771号
浙公网安备 33010602011771号