泊松分布
- 定义 若离散型随机变量X的分布为
 ,k=0,1,2,¼
其中常数l>0,则称X服从参数为l的泊松分布,记为
,k=0,1,2,¼
其中常数l>0,则称X服从参数为l的泊松分布,记为 。
。
- 泊松Poisson定理P41, 设有一列二项分布X
 ~B(
~B( ), n=1, 2, ...,如果
), n=1, 2, ...,如果 ,
,  为与n无关的正常数,则对任意固定的非负整数k,均有
为与n无关的正常数,则对任意固定的非负整数k,均有

证略。
例5:P43.
例6:P44,自学。
§2.3 随机变量的分布函数
一、概念
定义2.1
设X是一随机变量(不论是离散型还是非离散型),对任意的实数 ,令
,令
 (2.11)
(2.11)
则称F( )为X的分布函数。
)为X的分布函数。
例1:(书上例2.8)
设X服从参数为p的(0-1)分布,即: ,
, = 0,1,其中0<p<1,q=1-p.求X的分布函数F(
= 0,1,其中0<p<1,q=1-p.求X的分布函数F(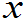 ).
).
例: 设R.V. X的分布函数为

求X的概率分布。
二、性质
性质1
若 1<
1< 2,则F(
2,则F( 1)£F(
1)£F( 2).即F(
2).即F( )是
)是 的单调不减函数。
的单调不减函数。
性质2
对任意的实数 ,均有
,均有
0£ F( )£1 (2.15)
)£1 (2.15)
且
 (2.16)
(2.16)
 (2.17)
(2.17)
性质3
对任意的实数 0,有
0,有
 (2.18)
(2.18)
即F( )在
)在 轴上处处右连续。
轴上处处右连续。
证明见P-44.
性质4 若F( )在X=
)在X= 0处连续,则P(X=
0处连续,则P(X= 0)=0
0)=0
性质5 P(a<X£b)=F(b)-F(a)
例: 设R.V.X的分布为

确定A ,且求P(-1< £2)
£2)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号