第七讲 矩阵级数与矩阵函数
一、 矩阵序列
1. 定义: 设有矩阵序列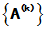 , 其中
, 其中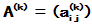 , 且当
, 且当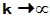 时
时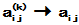 , 则称
, 则称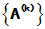 收敛, 并把
收敛, 并把 叫做
叫做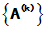 的极限, 或称
的极限, 或称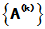 收敛于A. 记为
收敛于A. 记为
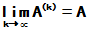 或
或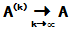
不收敛的序列则称为发散的,其中又分为有界和无界的情况.
2. 收敛矩阵序列的性质:
设 、
、 分别收敛于A、B, 则
分别收敛于A、B, 则
(1) 
(2) 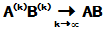
(3) 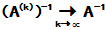 ,若
,若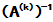 ,
,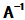 存在
存在
(4) 
3 收敛矩阵: 设A为方阵,且当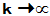 时
时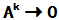 , 则称A为收敛矩阵.
, 则称A为收敛矩阵.
[定理] 方阵A为收敛矩阵的充要条件是A的所有特征值的模值均小于1.
证明: 对任何方阵A,均存在可逆矩阵P, 使得
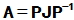
其中J为A的Jordan标准形
 ,
, 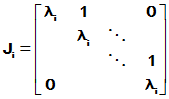
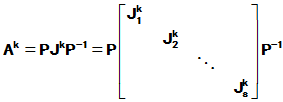
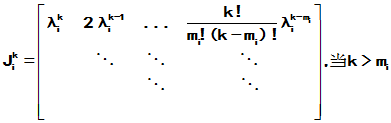
 就等价于
就等价于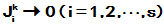 , 等价于
, 等价于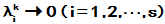 , 而这只有
, 而这只有 才可能也必能.
才可能也必能.
[得证]
二、 矩阵级数
1.定义: 矩阵序列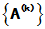 的无穷和
的无穷和 叫做矩阵级数, 而
叫做矩阵级数, 而 称为其部分和, 若矩阵序列
称为其部分和, 若矩阵序列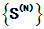 收敛,且有极限S, 则称该级数收敛,且有极限S. 记为
收敛,且有极限S, 则称该级数收敛,且有极限S. 记为

不收敛的级数必为发散的.
若矩阵级数 的所有元素
的所有元素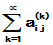 均绝对收敛,则称该级数为绝对收敛.
均绝对收敛,则称该级数为绝对收敛.
2. 绝对收敛矩阵的性质
- 绝对收敛级数一定收敛,且任意调换它的项所得的级数仍收敛,并具有相同的和.
(2) 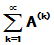 绝对收敛,则
绝对收敛,则 也绝对收敛且等于
也绝对收敛且等于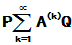
(3) 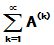 ,
, 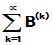 均绝对收敛,且和分别为
均绝对收敛,且和分别为 ,
,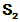 则
则
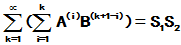
三、 方阵的幂级数
A为方阵, 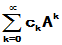 ,
, 称为A的幂级数.
称为A的幂级数. 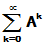 称为A的Neumann级数.
称为A的Neumann级数.
1. Neumann级数收敛的充要条件
[定理] Neumann级数收敛的充要条件是A为收敛矩阵,且在收敛时其和为 .
.
证明: [必要性]
级数 收敛, 其元素为
收敛, 其元素为
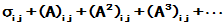
显然也是收敛的. 作为数项级数, 其通项趋于零是级数收敛的必要条件. 故
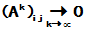 ,即
,即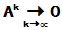
也就是说A为收敛矩阵.
[充分性]:
A为收敛矩阵, 则其特征值的模值均小于1. 设A的特征值为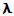 ,
, 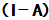 的特征值为
的特征值为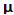 . 则由
. 则由
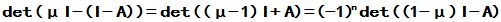
可见
故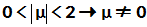 ,
, 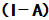 的行列式不为零,
的行列式不为零,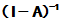 存在.
存在.
而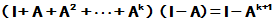
右乘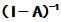 得
得
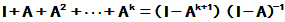
当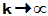 时,
时,  , 故
, 故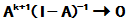 . 所以
. 所以

即Neumann级数收敛于 .
.
2. 收敛圆
[定理] 若矩阵A的特征值全部落在幂级数 的收敛圆内, 则矩阵幂级数
的收敛圆内, 则矩阵幂级数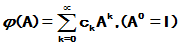 是绝对收敛的. 反之, 若A存在落在
是绝对收敛的. 反之, 若A存在落在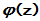 的收敛圆外的特征值, 则
的收敛圆外的特征值, 则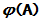 是发散的.
是发散的.
证明略.
[推论] 若幂级数在整个复平面上收敛, 则对任何的方阵A, 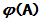 均收敛.
均收敛.
四、 矩阵函数
如:  , sinA, cosA
, sinA, cosA
以矩阵为自变量的" 函数"(实际上是"函矩阵")
我们知道, 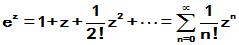

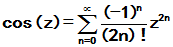
均为整个复平面上收敛的级数, 故对任何的方阵A
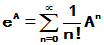
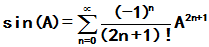
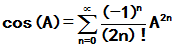
均绝对收敛. 三者分别称为矩阵指数函数、矩阵正弦函数、矩阵余弦函数。
[性质]


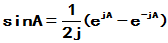
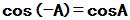


但是一般来说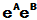 ,
,  ,
,  三者互不相等. 例如
三者互不相等. 例如
 ,
,  , 则
, 则
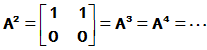
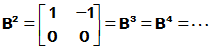
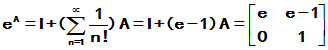


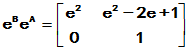
可见
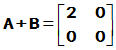 ,
, 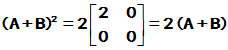 ,
, 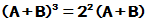 ,
,

所以, 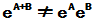 ,
, 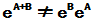
[定理] 若 , 则
, 则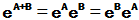
[证明]:
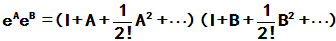
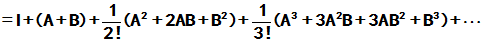
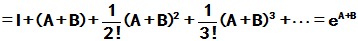
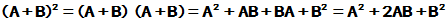
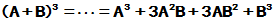
同理, 有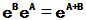
[推论]  ,
, 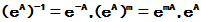 总存在逆阵
总存在逆阵
五、 矩阵函数的初步计算
1. Hamilton-Cayley定理
n阶矩阵A是其特征多项式的零点, 即令
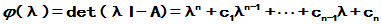
则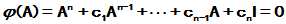
[证明]: 设A的特征值为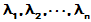 , 则
, 则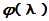 又可写成
又可写成
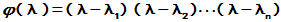
由Schur引理知, 存在酉矩阵U, 使得
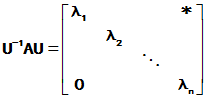
相似矩阵具有相同的特征多项式
所以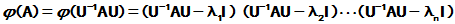


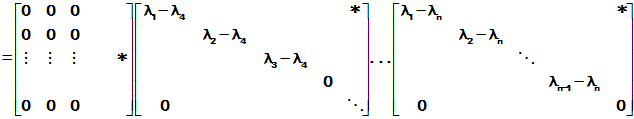
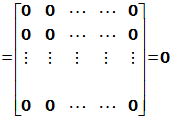
即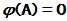
2.零化多项式
多项式f(z),若f(A)=0,则称其为A的零化多项式。
由以上定理可知,方阵A的特征多项式为A的零化多项式。
3. 矩阵指数函数、正弦函数、余弦函数的计算
例: 已知四阶矩阵的特征值是 、
、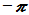 、 0、 0, 求sinA、 cosA、
、 0、 0, 求sinA、 cosA、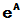
解: 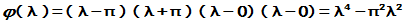
故
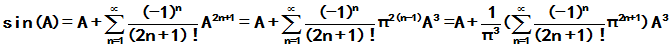
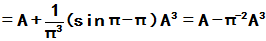
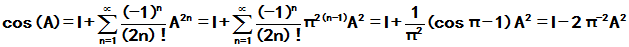
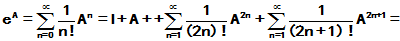

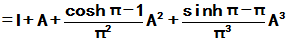
作业 P163 3, 4, 5




 浙公网安备 33010602011771号
浙公网安备 33010602011771号