第十二章 动量定理和动量矩定理
本章研究的两个定理
动量定理——力系主矢量的运动效应反映;
动量矩定理——力系主矩的运动效应反映。
- 质点系质量的几何性质
 质心
质心
质点系的质量中心,其位置有下式确定:

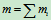
其投影式为
 ,
, 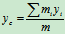 ,
, 
- 刚体对轴的转动惯量
定义:
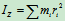 为刚体对
为刚体对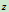 轴的转动惯量或
轴的转动惯量或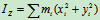

影响
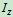 的因素
的因素 单位:
单位: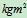
物理意义:描述刚体绕
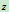 轴时惯性大小的度量。
轴时惯性大小的度量。
 的计算方法:
的计算方法:
- 积分法
例12.1已知:设均质细长杆为
 ,质量为
,质量为 。求其对于过质心且与杆的轴线垂直的轴
。求其对于过质心且与杆的轴线垂直的轴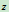 的转动惯量。
的转动惯量。

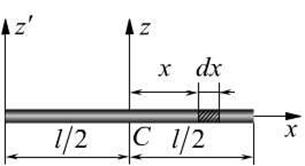
解:建立如图12.2所示坐标,取微段
 其质量为
其质量为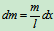 ,则此杆对轴
,则此杆对轴 的转动惯量为:
的转动惯量为: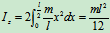
例12.2已知:如图12.3所示设均质细圆环的半径为
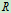 ,质量为
,质量为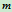 ,求其对于垂直于圆环平面且过中心
,求其对于垂直于圆环平面且过中心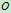 的轴的转动惯量。
的轴的转动惯量。

解:将圆环沿圆周分为许多微段,设每段的质量为
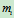 ,由于这些微段到中心轴的距离都等于半径
,由于这些微段到中心轴的距离都等于半径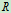 ,所以圆环对于中心轴
,所以圆环对于中心轴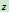 的转动惯量为:
的转动惯量为:
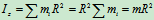
例12.3已知:如图12.4所示,设均质薄圆板的半径为
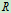 ,质量为
,质量为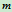 ,求对于垂直于板面且过中心
,求对于垂直于板面且过中心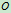 的轴
的轴 的转动惯量。
的转动惯量。

解:将圆板分成无数同心的细圆环,任一圆环的半径为
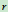 ,宽度为
,宽度为 ,质量为
,质量为 ,由上题知,此圆环对轴
,由上题知,此圆环对轴 的转动惯量为
的转动惯量为 ,于是,整个圆板对于轴
,于是,整个圆板对于轴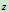 的转动惯量为:
的转动惯量为:
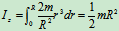
- 回转半径(惯性半径)
设刚体对轴
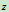 的转动惯量为
的转动惯量为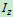 ,质量为
,质量为 ,则由式
,则由式 定义的长度,称为刚体对轴
定义的长度,称为刚体对轴 的回转半径。
的回转半径。
例如:均质杆(图12.2)
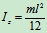
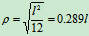
均质圆环(图12.3)
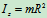

均质薄圆板(图12.4)
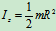
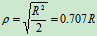
若已知刚体对轴的回转半径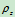 ,则刚体对轴
,则刚体对轴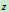 的转动惯量为:
的转动惯量为:
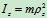
- 转动惯量的平行轴定理
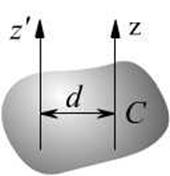
在图12.5中,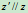 ,轴间距离为
,轴间距离为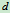 ,刚体质量为
,刚体质量为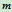 ,其中
,其中 轴过质心,则有
轴过质心,则有
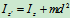
例如:在图12.2中,细长杆对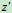 轴的转动惯量为
轴的转动惯量为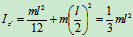
- 组合体
例12.4 已知:钟摆可简化为如图12.6所示。设均质杆和均质圆盘的质量分别为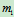 和
和 ,杆长为
,杆长为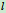 ,圆盘直径为
,圆盘直径为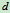 ,求钟摆对通过悬挂点
,求钟摆对通过悬挂点 的水平轴的转动惯量。
的水平轴的转动惯量。
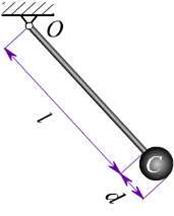
解:钟摆对水平轴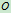 的转动惯量为:
的转动惯量为: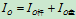
其中: 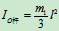
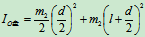
所以 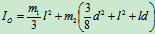
- 动量定理
- 动量的概念与计算
质点的动量为
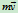
质点系的动量系为
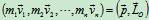
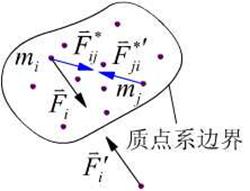
质点系的动量(动量系的主矢量)为
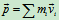
将质心公式
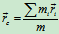 对时间
对时间 求一阶导数,有
求一阶导数,有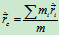 即
即
于是
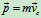
- 动量定理
1)质点的动量定理
设质点质量为
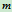 ,速度为
,速度为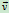 ,作用力为
,作用力为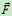 ,由牛顿第二定律,有
,由牛顿第二定律,有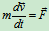
变换为
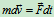 ——质点的动量定理的微分形式 (
——质点的动量定理的微分形式 (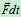 为元冲量)
为元冲量)
将上式对时间
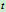 积分有
积分有
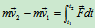 冲量 ——质点的动量定理的积分形式
冲量 ——质点的动量定理的积分形式
2)质点系的动量定理
设质点系由
 个质点组成,其中第
个质点组成,其中第 个质点的质量为
个质点的质量为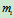 ,速度为
,速度为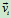 ,所受外力为
,所受外力为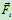 ,内力为
,内力为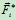 (图12.7)
(图12.7)
(1)由牛顿第二定律
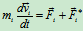
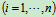
将上式由
 到
到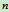 求和,有
求和,有
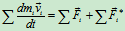
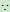
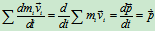 ,
,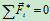
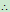
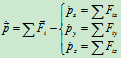 (Ⅰ)
(Ⅰ)
由
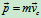 ,
, 
质心运动定理:
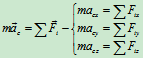 (Ⅱ)
(Ⅱ)
质心运动定理反映了质心的重要力学特征:质点系的质心的运动只取决于质点系的外力,内力改变不了质心的运动。这个定理在理论上和实际中都具有重要的意义。
在求解刚体系统动力学问题时,为了应用方便,常将上式改写为
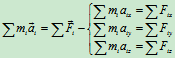 (Ⅲ)
(Ⅲ)
式中
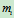 、
、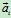 分别是刚体系统中第
分别是刚体系统中第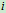 个刚体的质量和质心加速度。
个刚体的质量和质心加速度。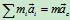 是由质心公式对时间求二阶导数后得到的,即
是由质心公式对时间求二阶导数后得到的,即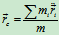
- 积分形式
由式(Ⅰ)可得到积分形式

- 动量守恒(质心守恒)
若
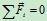 则
则 常矢量 或
常矢量 或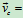 常矢量
常矢量
若
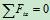 则
则 常量 或
常量 或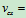 常量
常量
若
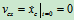 则
则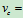 常量 (质心守恒)
常量 (质心守恒)
实例分析
实例1利用质心运动定理解释定向爆破
实例2利用质心运动定理分析汽车的起动与刹车

例12.5已知:如图12.11所示的电动机用螺栓固定在刚性基础上,设其外壳和定子的总质量为
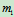 ,质心位于转子转轴的中心
,质心位于转子转轴的中心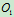 ;转子质量为
;转子质量为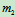 ,
,
由于制造或安装是的偏差,转子质心
 不在转轴中心上,偏心距
不在转轴中心上,偏心距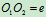 。转子以等角速度
。转子以等角速度 转动,试求电动机机座的约束力。
转动,试求电动机机座的约束力。
解:
- 研究对象:电动机整体
- 分析受力(如图示)

- 分析运动:定子不动
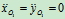 ;转子作匀速圆周运动,其法线加速度
;转子作匀速圆周运动,其法线加速度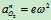
- 列动力学方程求解:
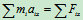
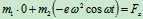
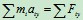

由此解出:
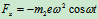
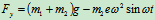
- 讨论
- 机座的约束力由两部分组成,一部分由重力(主动力)引起的,称为静约束力(静反力),另一部分是由于转子质心运动状态变化引起的,称为附加动约束力。
- 附加动约束力有最大值或最小值:
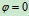 时,
时,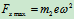
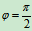 时,
时,
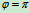 时,
时,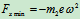
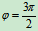 时,
时,
- 附加动约束力与成正比,当转子的转速很高时,其数值可以达到静约束力的几倍,甚至几十倍,而且这种约束力是周期性变化的,必然引起机座和基础的振动,还会引起有关构件内的交变应力。
- 利用动量定理能否求约束力偶矩
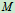 ?
?
本例也可以选用质心运动定理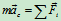 求解。
求解。
在图12.10中,因为定子不动,故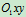 是惯性参考系中,写出系统的质心坐标公式:
是惯性参考系中,写出系统的质心坐标公式: 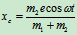
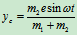
将上两式对时间求二阶导数,可得:
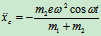
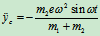
由质心运动定理:

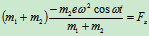
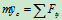
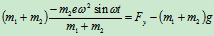
可得
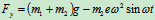
例12.6 在上例中(例12.5),若电动机机座与基础之间无螺栓固定,且为光滑接触(图12.12),初始时电动机静止。求转子以等角速度 转动时电机外壳的运动,并分析电机跳起的条件。
转动时电机外壳的运动,并分析电机跳起的条件。

解:1)求电机外壳的运动
研究电机整体 由图示受力分析知 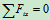 又因为
又因为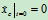 故
故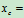 常量
常量
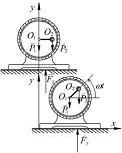
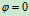 时,由图12.11
时,由图12.11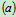
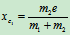
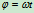 时,由图12.11
时,由图12.11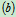

因为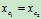 解得:
解得: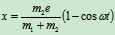
说明电机沿水平方向作简谐振动,振幅为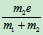
2) 电机未跳起时,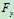 仍可用上例所求结果,即
仍可用上例所求结果,即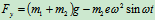
令 ,求的电机的角速度为:
,求的电机的角速度为: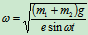
讨论:当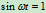 ,即
,即 时,转子质心
时,转子质心 在最高处,可求得使电机跳起的最小角速度为:
在最高处,可求得使电机跳起的最小角速度为:
例12.7已知:如图12.13表示水流流经变截面弯管的示意图。设流体是不可压缩的理想流体,而且流动是定常的。求流体对管壁的作用力。
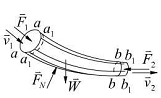
解:1)研究对象:取管中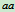 截面和
截面和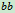 截面之间的流体为研究的质点系
截面之间的流体为研究的质点系
2)受力分析:如图所示

设流体密度为 ,流量为
,流量为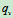 ,(流体在单位时间内流过截面的体积流量,定常流动时,
,(流体在单位时间内流过截面的体积流量,定常流动时, 是常量)在
是常量)在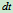 时间内,流过截面的质量为
时间内,流过截面的质量为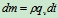 ,其动量改变量为
,其动量改变量为
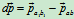
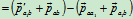
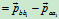
即 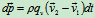
由 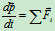
得 
令 
其中 为管子对流体的静约束力,由下式确定
为管子对流体的静约束力,由下式确定
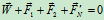
则有 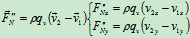
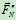 为流体流动时,管子对流体的附加动约束力。可见,当流体流速很高或管子截面积很大时,流体对管子的附加动压力很大,在管子的弯头处必须安装支座(图12.14)
为流体流动时,管子对流体的附加动约束力。可见,当流体流速很高或管子截面积很大时,流体对管子的附加动压力很大,在管子的弯头处必须安装支座(图12.14)
三 动量矩的概念及其计算
- 质点的动量矩
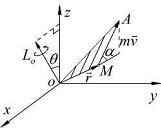
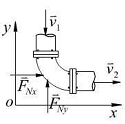
设质点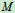 的质量为
的质量为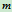 ,某瞬时的速度为
,某瞬时的速度为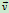 ,到
,到 点的矢径为
点的矢径为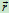 (图12.15)
(图12.15)
质点对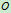 点的动量矩为
点的动量矩为 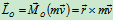
质点对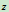 轴的动量矩为
轴的动量矩为 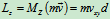
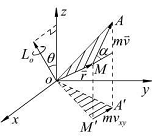
质点对 点和
点和 轴(该轴通过
轴(该轴通过 点)的动量矩关系为
点)的动量矩关系为 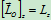
- 质点系的动量矩
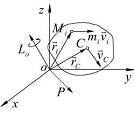
设质点系由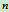 个质点组成,其中第
个质点组成,其中第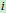 个质点的质量为
个质点的质量为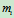 ,速度为
,速度为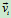 ,到
,到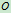 点的矢径为
点的矢径为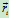 ,则质点系对
,则质点系对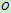 点的动量矩(动量系对点的主矩)为:
点的动量矩(动量系对点的主矩)为:
质点对 轴的动量矩为
轴的动量矩为 
动量矩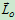 的解析式为
的解析式为 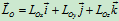
刚体动量矩的计算
- 刚体平动(图12.17)

- 定轴转动刚体对转轴的动量矩(图12.18)

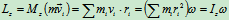
3)平面运动刚体对其平面内一点的动量矩(图12.19)

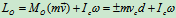
例12.8已知:质量为,的两物块分别系在两柔软不可伸长的绳子上,图12.20所示,此两绳分别绕在半径为和并固结在一起的鼓轮上,设鼓轮的质量为,对转轴的回转半径为,并以转动。求系统对鼓轮转轴的动量矩。
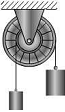
解:
- 分析运动:
- 计算
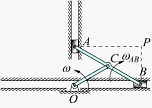
例12.9图12.21所示椭圆规尺,质量为,曲柄质量为,滑块和的质量为,设曲柄和均为均质杆,且,曲柄以转动,求:此椭圆规尺机构对转轴的动量矩。
解:
- 分析运动:规尺作平面运动
- 计算
物块速度均通过转轴 ,对的动量矩为,杆定轴转动,对轴的动量矩为
 心为定点的动量矩定理
心为定点的动量矩定理
引言:求均质轮在外力偶的作用下,绕质心轴的角加速度
- 质点对固定点的动量矩定理图12.22
牛顿第二定律:
上式两边左叉矢径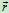
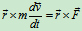
左边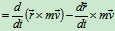
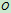 是固定点时,于是有
是固定点时,于是有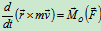
——质点对固定点的动量矩定理
- 质点系对固定点的动量矩定理
设质点系由个质点组成,其中第个质点的质量为,速度为,对固定点的矢径为,作用在该质点上的外力为,内力为。
第个质点对固定点的动量矩定理为
将上式从到求和
由图12.23知
右边
左边
可得 质点系对固定点的动量矩定理
- 动量矩守恒
若,常矢量
若 则常量
例12.10分析受有心力作用的物体的运动
解:如图12.24所示,因为
故常矢量,可见质点在有心力作用下运动的轨迹是平面曲线。
例12.11 如图12.25所示,在调速器中,除小球外,各杆重量可不计,忽略摩擦,系统绕轴自由转动。初始时,系统的角速度为,当细绳拉断时。求各杆与铅直线成角时系统的角速度。
解:研究整体:因重力和轴承力对于转轴的矩为零,即 故常量
时
时
由 得
例12.12已知:不可伸长的绳子绕过不计质量的定滑轮,绳的一端悬挂物块,另一端有一个与物块重量相等的人,从静止开始沿绳子上爬,设其相对绳子的速度为,试问:物是否动?并分析绳子的速度。
解:研究整体系统:因为,故常量
设轮顺时针转,绳子的速度为
则
由 即
得
物上升的速度为
人向上的速度为
人、物向上的绝对速度大小相等,方向相同,人物同时到达顶端。
五.刚体定轴转动微分方程
设刚体在主动力系作用下,绕固定轴转动(图12.27),设刚体对轴的转动惯量为,瞬时的角速度为,刚体对转轴的动量矩为,由质点系对固定轴的动量矩定理
可得
刚体的定轴转动微分方程
例12.13 已知复摆由绕水平轴转动的刚体构成,已知复摆的重量为,重心到转轴的距离为,如图12.28所示,设复摆对转轴的转动惯量为。求复摆微摆动的周期。
解:
- 研究对象:复摆
- 分析受力:如图12.28所示
- 分析运动:复摆作定轴转动,用表示其转角
- 列动力学方程,求解:
由题意,复摆微摆动时,于是有
这是简谐运动的标准微分方程,此方程的解为:
式中称为角振幅,为初相位他们由初始条件确定
摆动周期为
- 讨论
- 若测出周期T,可求出刚体对转轴的转动惯量
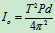
- 如果要求轴承O的约束力
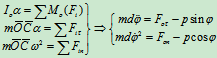
求,积分求
求轴承的约束力
刚体定轴转动微分方程组
例12.14 已知:电动机将不变转矩M加在轴上(图12.29)轴通过节圆半径为 的外啮合齿轮传动给轴Ⅱ。轴Ⅱ与提升重物的鼓轮固结为一体,鼓轮半径为R,轴Ⅰ连同其上零件对轴的转动惯量为
的外啮合齿轮传动给轴Ⅱ。轴Ⅱ与提升重物的鼓轮固结为一体,鼓轮半径为R,轴Ⅰ连同其上零件对轴的转动惯量为 ,轴Ⅱ连同其上零件对轴的转动惯量为
,轴Ⅱ连同其上零件对轴的转动惯量为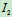 ,且各自重心分别在转轴上。重物的质量为,不计摩擦。求:重物A的加速度。
,且各自重心分别在转轴上。重物的质量为,不计摩擦。求:重物A的加速度。
解:
- 研究轴Ⅰ(图12.29)

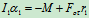 (1)
(1)
- 研究轴物(图12.29)
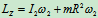
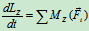
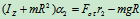 (2)
(2)
- 运动学关系
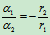 (3)
(3)
 (4)
(4)
由方程(1)、(2)、(3)、(4),解得:
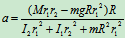
- 矩心为质心的动量矩定理
- 质点系对于定点"O"和质心"C"的动量矩之间的关系
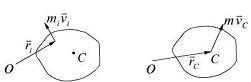
如图12.30所示,O为定点,C为质点系的质心,质点系对于定点O的动量矩为
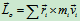
对于任一质点 ,由图可见
,由图可见

于是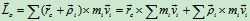
式中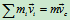 ,
,  质点系对于质心的绝对动量矩
质点系对于质心的绝对动量矩
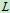
图12.30中为随质心平动的参考系,设点相对该坐标系的速度为,有
式中质点系对于质心的相对动量矩
有
代入式,有
- 质点系相对于质心的动量矩定理
质点系相对于固定点的动量矩定理
左边
右边
由于
所以
矩心为质心的动量矩定理
若
则 常矢量 矩心为质心的动量矩守恒
试分析跳水运动的腾空动作(图12.31)
刚体的平面运动微分方程
设刚体具有质量对称平面,作用在刚体上的力系可以简化为在此平面内的力系,如图12.31所示。以为基点建立平动坐标系,则刚体相对于此质心的动量矩为
刚体平面运动岁质心平动相对质心转动
随质心平动
相对质心转动
刚体平面运动微分方程:
例12.15 已知:质量为半径为的均质圆轮放在倾角为的斜面上,由静止开始运动。设轮沿斜面作纯滚动。求:(1)轮心的加速度,(2)轮沿斜面不打滑的条件。
解:
- 研究对象:轮
- 分析受力:如图12.33所示
- 分析运动:轮作平面运动,轮心沿斜面作直线运动
- 列动力学方程求解:
轮纯滚动
联立解得:
纯滚动的条件:
- 讨论:若,由式 得,常量 轮平动
若,则轮沿斜面打滑,此时
由方程 可求得
例12.16 已知:均质细杆质量,长度,端用两条细绳悬挂,三者个夹角,如图12.34所示。求:剪断绳时,杆的角加速度及绳的拉力。
解:
- 研究对象:杆
- 分析受力:如图12.34所示
- 分析运动:剪断绳时,杆作平面运动。质心作平面曲线,轨迹未知。
- 列动力学方程,求解:
以上三个式中有个未知量,补充一个运动学关系
以上四式联立,解得:
代入数据,得:
例12.17 已知:质量为半径为的均质圆轮,可以在半径为的圆弧轨道中作纯滚动(如图12.34所示),时圆轮由静止释放。求:(1)接触处的摩擦力和正压力
(2)微运动的周期与运动规律
解:
1.研究对象:圆轮
2.分析受力:如图12.35所示
3.分析运动:轮作平面运动,轮心沿作圆周运动
4.列动力学方程,求解:
- 求
- 微运动时
由式 令
解得
所以
周期




 浙公网安备 33010602011771号
浙公网安备 33010602011771号