Cicada
Question
问题描述
深海龙王准备抓几只知了送给水葫芦娃。他发现面前的这棵树是一颗以1号节点为根节点的一颗有根树,同时他又发现这颗树上的每一个节点i上都恰好停有一只蝉,正在愉快的以ai的响声鸣叫~
深海龙王会从1号节点起沿着树边一直爬,直到爬到一个叶子节点(请不要在意他怎么下来),在这途中他可以选择一些他经过的蝉并将它们抓起来。但是水葫芦娃希望深海龙王抓的知了能发出越来越响的鸣叫声,起码得要单调不减!
输入格式
第1行包含一个整数n,表示树上的结点个数;
第2行包含n - 1个整数,分别代表第2到n号节点的父亲节点编号;
第3行包含n个整数ai,代表i号节点知了的响声。
输出格式
一行一个整数,表示深海龙王最多能抓到的知了数。
样例输入
11
1 1 1 2 2 6 7 3 3 10
6 5 2 2 6 4 3 2 10 2 3
样例输出
3
数据

样例说明
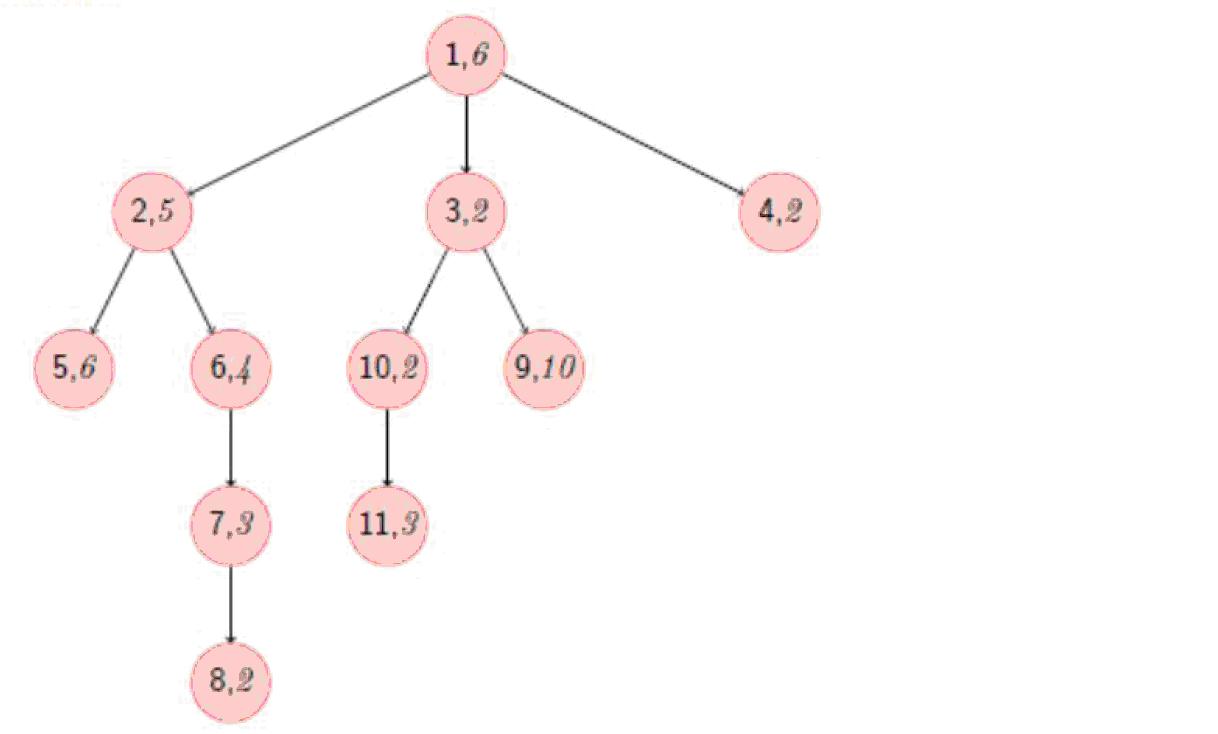
最优路线为1 -> 3 -> 10 -> 11,能抓到的知了为3,10,11共3只
Analysis
一眼可以看出这个题目是个树上动规,大概意思就是在树上找最长不下降子序列,求长度。
首先,显而易见的暴力思路是将树转化成链,枚举每一条链,对链做最长不下降子序列。这是我当时第一次考试时候写的方法,第二次考试懒得写了……
时间复杂度O(叶子节点数*叶子对应链的长度^2),大概也就O(n^2)远远小于O(n^3)差不多,具体求出渐进时间复杂度就复杂了,需要各种不等式……我就不分析了。反正肯定拿不到全分,不过20分保底。
Code A 30
#include<bits/stdc++.h>
using namespace std;
vector<int>A[100010];
int val[100010],S[100010],last[100010],dp[100010],ans;
void cal(int n){
memset(dp,0,sizeof(dp));
for (int i=1;i<=n;++i){
for (int j=1;j<i;++j){
if (last[j]<=last[i])
dp[i]=max(dp[i],dp[j]+1);
}
dp[i]=max(1,dp[i]);
ans=max(ans,dp[i]);
}
}
void dfs(int k,int len){
last[len]=val[k];
if (!S[k]){//叶子节点
cal(len);
return ;
}
for (int i=0;i<S[k];++i)
dfs(A[k][i],len+1);
}
int main(){
freopen("cicada.in","r",stdin);
freopen("cicada.out","w",stdout);
int n;
cin>>n;
int x;
for (int i=2;i<=n;++i){
cin>>x;
A[x].push_back(i);
}
for (int i=1;i<=n;++i)
cin>>val[i];
for (int i=1;i<=n;++i)
S[i]=A[i].size();
dfs(1,1);
cout<<max(1,ans)<<endl;
return 0;
}
很显然求最长不下降子序列那个地方可以优化到O(nlogn),具体代码如下。
Code B 40
#include<bits/stdc++.h>
using namespace std;
vector<int>A[100010];
int val[100010],S[100010],last[100010],dp[100010],ans;
int search(int i,int len){
int f,p,mid;
f=0,p=len;
while (p-f>1){
mid=(p+f)/2;
if (dp[mid]>last[i])
p=mid;
else
f=mid;
}
return f+1;
}
void cal(int n){
memset(dp,0,sizeof(dp));
dp[1]=last[1];
int len=1,pos;
for (int i=2;i<=n;++i){
if (last[i]>=dp[len])
dp[++len]=last[i];
else{
pos=search(i,len);
dp[pos]=last[i];
}
}
ans=max(ans,len);
}
void dfs(int k,int len){
last[len]=val[k];
if (!S[k])//叶子节点
cal(len);
for (int i=0;i<S[k];++i)
dfs(A[k][i],len+1);
}
int main(){
freopen("cicada.in","r",stdin);
freopen("cicada.out","w",stdout);
int n;
cin>>n;
int x;
for (int i=2;i<=n;++i){
cin>>x;
A[x].push_back(i);
}
for (int i=1;i<=n;++i)
cin>>val[i];
for (int i=1;i<=n;++i)
S[i]=A[i].size();
dfs(1,1);
cout<<max(1,ans)<<endl;
return 0;
}
注意,在search函数中我使用的是>而不是>=,实际上,只能使用不带等于号的,具体为什么我也不清楚,反正二分法这种有开闭区间的都必须这样,不然有可能错。基于同样的道理,在使用stl中的sort函数时,如果传入cmp函数,必须使用不带等于号的!
然后还能怎么优化呢?
很显然,由于我们把树依据叶子划分成了链,不同叶子对应的“枝条”其实是有重复部分的。我们要想办法避免这个重复部分的计算。
很显然,我们可以边搜索,加入last,边计算dp。但这样的话,last数组甚至不再需要了,我们只需要计算出当前视当前节点为叶子节点的dp长度即可。
注意,在计算完当前节点,递推解答当前节点的儿子节点之后,必须要把dp数组恢复成计算这次之前的情况,这十分重要!我在这个地方坑了很久,才发现,dp是全局变量,由于深搜的搜索顺序是一直向下搜的,dp会被更改,然而当一个节点有多个儿子时如果被更改就不对了!
Code AC
#include<bits/stdc++.h>
using namespace std;
vector<int>A[100010];
int val[100010],S[100010],dp[100010],ans=1;
int search(int i,int f,int p){
int mid;
while (p-f>1){
mid=(p+f)/2;
if (dp[mid]>val[i])
p=mid;
else
f=mid;
}
return f+1;
}
void dfs(int k,int len){
int pos=0,temp;
if (k==1)
dp[1]=val[1];
else{
if (dp[len]<=val[k])
dp[++len]=val[k];
else{
pos=search(k,0,len);
temp=dp[pos];
dp[pos]=val[k];
}
}
ans=max(ans,len);
for (int i=0;i<S[k];++i)
dfs(A[k][i],len);
dp[pos]=temp;
}
int main(){
freopen("cicada.in","r",stdin);
freopen("cicada.out","w",stdout);
int n;
cin>>n;
if (n==1){
cout<<1<<endl;
return 0;
}
int x;
for (int i=2;i<=n;++i){
cin>>x;
A[x].push_back(i);
}
for (int i=1;i<=n;++i)
cin>>val[i];
for (int i=1;i<=n;++i)
S[i]=A[i].size();
dfs(1,1);
cout<<ans<<endl;
return 0;
}
我还设计出了第二种算法,和之前这个算法有常数上的区别。
我们很容易发现code B超时的原因是重复计算。由于我们是以叶子节点为链尾,根节点为链头,把树划分成一条一条的链,不同叶子节点对应的链只有唯一一条,但是这些链之间具有大量的重复,就是开头的一部分,这一部分在动规中被我们重复计算了很多次!我们应该避免掉这部分重复计算。
很容易想到这样的一个算法:
我们不再仅仅把根视为链头,叶子节点视为链尾,而是以两个在同一条链上的相邻的分支节点为链头链尾,当遇到分支节点的时候就把上一个分支节点到这一个分支节点之间的dp算出来(这两个分支节点之间形成一条链),然后反复这样递推下去即可。
以题目给的图为例:

在原本的code B中,我们把1->5视为一条完整的链,但是在这个算法中,这条链被拆分为1->2和2->5两条(实现中要注意左开右闭等等细节),而原本的1->8则被拆分为1->2和2->8两条链。可以发现现在这个算法避免重复计算了1->2这条短链,这就是这个算法优化的地方。
当然,这个算法比之前的算法复杂一些(主要是左开右闭这个问题,还有dp还原),实践中并不推荐使用,但是这是一种很重要的思想方法,把整体划分成部分,进而减少掉重复计算,这需要注意,这个思想方法在很多问题中有更高深的应用。
代码我没打出来……把dp还原那个地方实在不想改了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号