各种排序算法

1.插入排序

从第二个元素开始，和前面的元素比较，如果后面的小于前面的，就交换两个元素位置

    public static void sort11(int[] a) {

       int j;

       int temp;

       for (int i = 1; i < a.length; i++) {

           j = i;

           while (a[j] < a[j - 1] && j > 1)  {

               temp = a[j - 1];

               a[j - 1] = a[j];

               a[j] = temp;

               j--;

           }

       }

    }

 

2.折半插入

在插入第i个元素时，对前面的0～i-1元素进行折半，先跟他们中间的那个元素比，如果小，则对前半再进行折半，否则对后半进行折半，直到left>right，然后再把第i个元素前1位与目标位置之间的所有元素后移，再把第i个元素放在目标位置上

  public static void erfenpaixu(int[] a) {

       for (int i = 1; i < a.length; i++) {

           int temp = a[i];

           int low = 0;

           int high = i - 1;

           while (low <= high) {

               int mid = (low + high) / 2;

               if (temp > a[mid]) {

                  low = mid + 1;

               } else {

                  high = mid - 1;

               }

           }

           for (int j = i - 1; j > high;  j--) {

               a[j + 1] = a[j];

           }

           a[high + 1] = temp;

       }

    }

 

 

 

 

3.冒泡排序

取第一个元素与后一个比较，如果大于后者，就与后者互换位置，不大于，就保持位置不变。再拿第二个元素与后者比较，如果大于后者，就与后者互换位置。一轮比较之后，最大的元素就移动到末尾。相当于最大的就冒出来了。再进行第二轮，第三轮，直到排序完毕。

    public static void MaoPai(int[] a) {

       for (int i = 0; i < a.length; i++) {

           for (int j = 0; j < a.length - i  - 1; j++) {

               if (a[j] > a[j + 1]) {

                  int temp = a[j + 1];

                  a[j + 1] = a[j];

                  a[j] = temp;

               }

           }

       }

    }

 

插入排序和冒泡排序的区别： 插入排序越往后面，动静越大，因为涉及到的元素越来越多；冒泡排序越往后面，动静越小，因为涉及到的元素越来越少。

 

4.快速排序

快速排序,说白了就是给基准数据找其正确索引位置的过程.

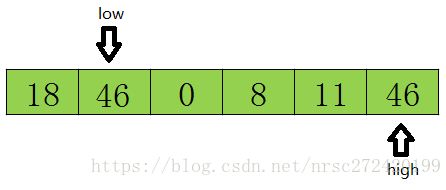
如下图所示,假设最开始的基准数据为数组第一个元素23,则首先用一个临时变量去存储基准数据,即tmp=23;然后分别从数组的两端扫描数组，设两个指示标志:low指向起始位置，high指向末尾.

首先从后半部分开始，如果扫描到的值大于基准数据就让high减1,如果发现有元素比该基准数据的值小(如上图中18<=tmp)，就将high位置的值赋值给low位置 ,结果如下:

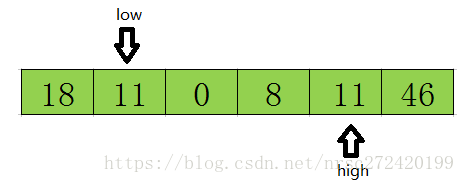
然后开始从前往后扫描,如果扫描到的值小于基准数据就让low加1,如果发现有元素大于基准数据的值(如上图46=>tmp)，就再将low位置的值赋值给high位置的值,指针移动并且数据交换后的结果如下:

然后再开始从后向前扫描,原理同上,发现上图11<=tmp,则将low位置的值赋值给high位置的值,结果如下:

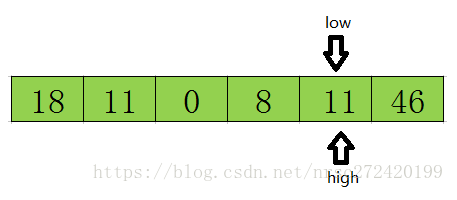
然后再开始从前往后遍历,直到low=high结束循环,此时low或high的下标就是基准数据23在该数组中的正确索引位置.如下图所示.

这样一遍走下来,可以很清楚的知道,其实快速排序的本质就是把基准数大的都放在基准数的右边,把比基准数小的放在基准数的左边,这样就找到了该数据在数组中的正确位置.

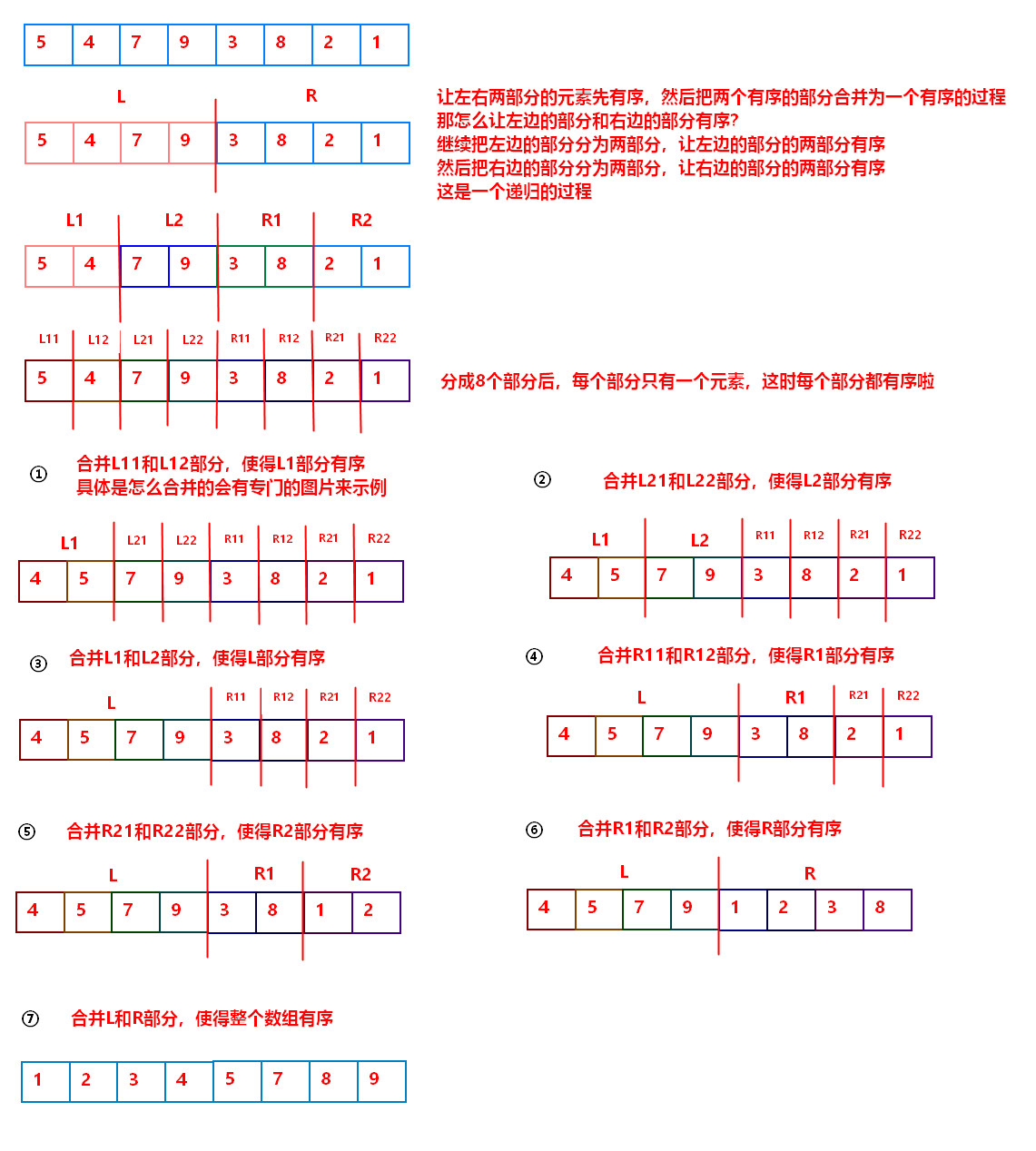
以后采用递归的方式分别对前半部分和后半部分排序，当前半部分和后半部分均有序时该数组就自然有序了。

public static void quickSort(int[] a, int  low, int high) {

       if (low < high) {

           int index = getIndex(a, low,  high);

           quickSort(a, low, index - 1);

           quickSort(a, index + 1, high);

       }

    }

    public static int getIndex(int[] a, int  low, int high) {

       int temp = a[low];

       while (low < high) {

           while (high > low && a[high] >=  temp) {

               high--;

           }

           a[low] = a[high];

           while (high > low && a[low] <=  temp) {

               low++;

           }

           a[high] = a[low];

       }

       a[low] = temp;

       return low;

    }

 

5.选择排序

1. 思想：每次从未排序的序列中选择一个最小的数未排序序列第一个数交换，相当于每次从未排序的序列中选择一个最小的数放到排好序的序列最后一个位子，当未排序序列为空的时候整个序列即为有序

 

2. 举例：例如序列8 7 3 4 5 0 1

 

    第一次：序列 8 7 3 4 5 0 1，未排序序列最小的数0，和8交换，此时排好序序列为0

 

    第二次：序列 0 7 3 4 5 8 1，未排序序列最小的数1，和7交换，此时排好序序列为0 1

 

    第三次：序列 0 1 3 4 5 8 7，未排序序列最小的数3，本身不用交换，此时排好序序列为0 1 3

    public static void chooseSort(int[] a) {

       for (int i = 0; i < a.length; i++) {

           int temp = i;

           for (int j = i + 1; j < a.length;  j++) {

               if (a[j] < a[temp]) {

                  temp = j;

               }

           }

           int temp1 = a[i];

           a[i] = a[temp];

           a[temp] = temp1;

       }

 

6.堆排序

 

7.归并排序

（1）流程

（2）合并两个有序数组

 

    public static void guiBingSort(int[] a,  int start, int end, int mid) {

       int[] temp = new int[end - start +  1];

       int p1 = start;

       int p2 = mid + 1;

       int i = 0;

       while (p1 <= mid && p2 <= end) {

           if (a[p1] < a[p2]) {

               temp[i] = a[p1];

               p1++;

           } else {

               temp[i] = a[p2];

               p2++;

           }

           i++;

       }

       while (p1 <= mid) {

           temp[i] = a[p1];

           i++;

           p1++;

       }

       while (p2 <= end) {

           temp[i] = a[p2];

           i++;

           p2++;

       }

       for (int j = 0; j < temp.length;  j++) {

           a[start + j] = temp[j];

       }

    }