对角矩阵压缩

尝试对角矩阵的压缩

矩阵元素a_ij的下标i、j与其存储在数组中的位置下标k（从0开始计数）存在如下的对应关系：当i=1时，k=j-1(1≤j≤2)；当i＞1时，k=2×i+j-3(|i-j|≤1)。
　　① 当i=1时，j的取值就是矩阵元素a_ij在数组中的存储次序，数组中存储下标为次序减1，故k=j-1。
　　② 当i＞1时，在矩阵元素a_ij之前已经存储了i-1行矩阵元素和第i行的j-i+1个元素，又已知矩阵的第1行需要存储2个元素，第2～i-1行均需要存储3个元素，故矩阵元素a_ij之前一共存储的元素数有2+(i-1-2+1)×3+(j-i+1)=2×i+j-3。故aij的存储下标为2×i+j-3。

 

 

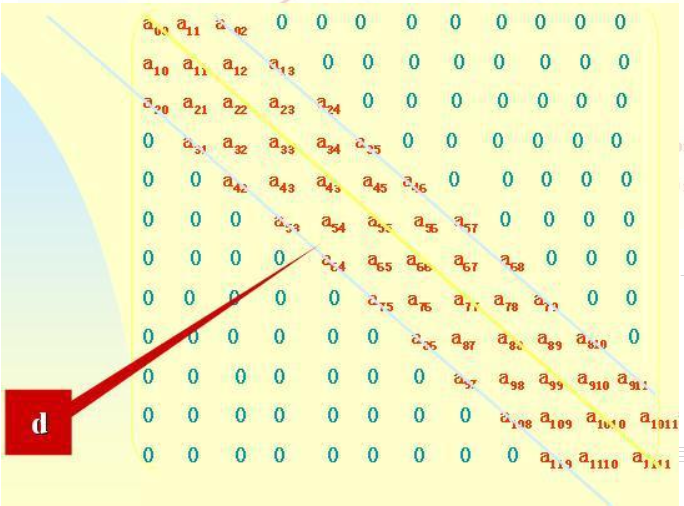
非零元素仅出现在主对角上(aii，0≤i≤n-1)，对角线上面的那条线上和下面的那条线上

当|i-j|>1时，元素aij=0。
    　由此可知，一个k对角线矩阵(k为奇数)A是满足下述条件的矩阵：

 若|i-j|>(k-1)／2，则元素aij=0。
　　　若|i-j|<=(k-1)／2  
　　　 　对角矩阵可按行优先顺序或对角线的顺序，将其压缩存储到一个向量中，并且也能找到每个非零元素和向量下标的对应关系。

这里若|i-j|>(k-1)／2，则元素aij=0。