重试语义下的幂等性与正确性

在分布式系统中，重试是默认常态而非边缘情况（edge case）。网络超时、进程重启、部分失败意味着：即使客户端行为完全正确，同一个逻辑请求也可能被执行多次。

本文解释系统如何为非幂等操作实现 幂等性（idempotency），并以“创建群组（group creation）”作为具体例子。重点在于当重试不可避免发生时，如何保持系统的正确性（correctness）。

为什么幂等性是一等关注点

创建一个群组涉及：

• 生成新的标识符
• 创建多个领域记录
• 建立群主归属与会话状态

如果同一个请求在缺乏保护的情况下被处理两次，系统将创建两个不同的群组。这不是性能问题，而是一个正确性违规（correctness violation）。一旦接受 at-least-once 执行语义，幂等性就不可回避。

核心设计问题

系统必须回答一个看似简单的问题：

如果同一个请求被执行多次，我们如何确保结果要么被复用，要么被安全拒绝？

解决方案受到几个约束：

• 领域校验在上游已假定正确
• 请求可能被并发重试
• 基础设施失败可能在任何时刻中断执行
• 我们希望方案简单、显式，并局部化在单个用例中

最终系统采用了一个带 key 的幂等协议（keyed idempotency protocol），作用域限定在单个操作上。

具体实现

 

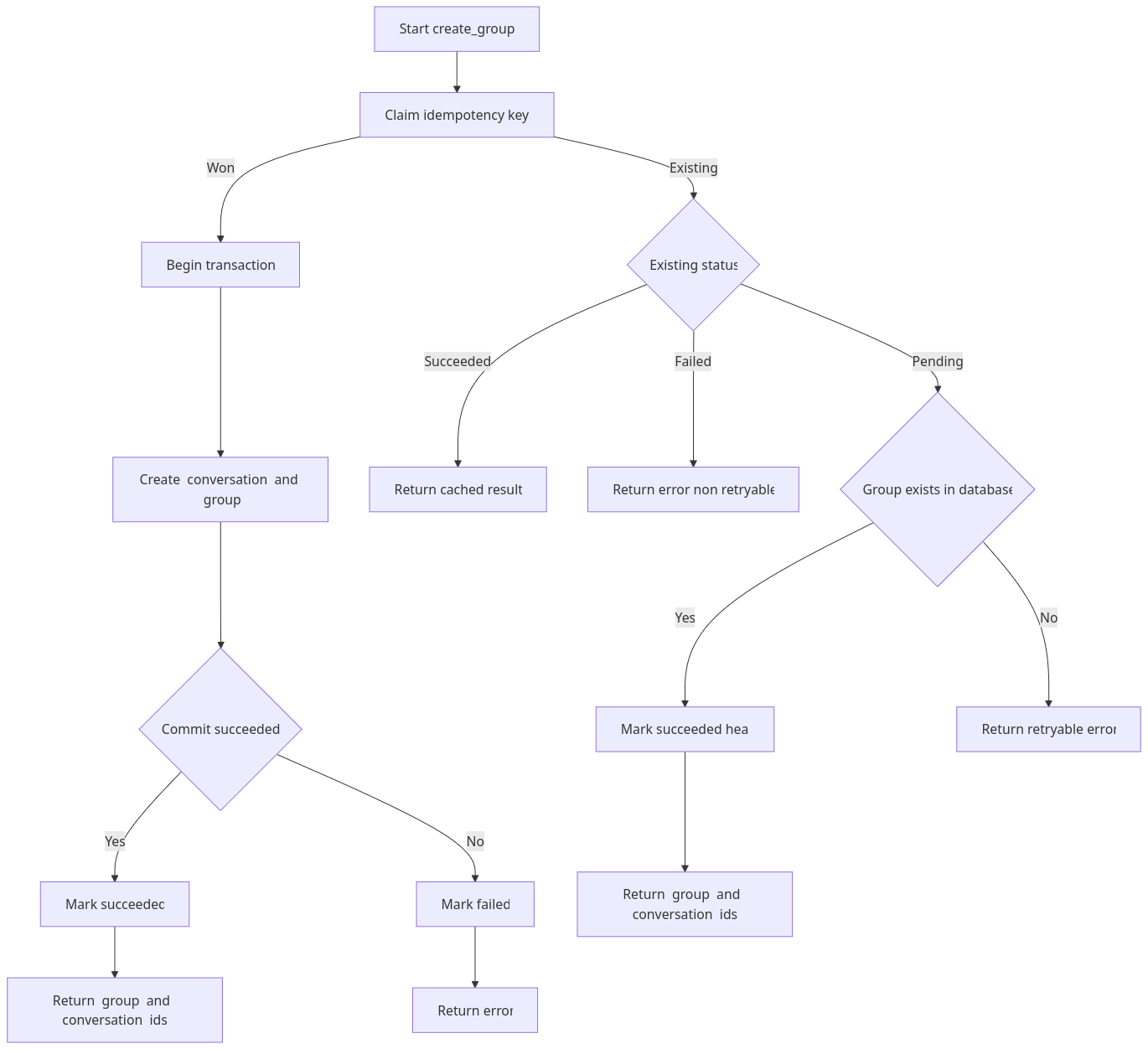
幂等性作为显式协议

对于群组创建，客户端需要提供一个 幂等 key（idempotency key）。这个 key 标识的是一次 attempt（尝试），而不是抽象意义上的“意图请求”。

系统内部为每个 key 维护三种状态：

• Pending（进行中） —— 该 attempt 可能提交了，也可能没有
• Succeeded（成功） —— 群组已成功创建
• Failed（失败） —— attempt 已终结，不允许再重试

核心思想是：

只有一个执行路径可以“获胜”，并真正执行领域写入。

Claim：获得执行权

当 create_group 请求到达时：

• 服务首先尝试 claim 该幂等 key
• 如果 claim 成功，该请求成为 leader
• 如果 key 已存在，该请求成为 follower

这一步在不需要全局锁的情况下建立了互斥性，协调范围仅限数据库。

Leader 的职责

获胜的执行负责：

• 完成所有领域写入
• 保证群组与会话创建的原子性
• 记录 attempt 的最终结果

如果事务提交成功：

• 幂等记录标记为 Succeeded
• 创建出的 identifiers 会被缓存，以便未来重试复用

如果在提交前失败：

• 幂等记录标记为 Failed

这里有一个关键规则：

只有在“确认没有 commit 发生”时，才允许写入 Failed。

违反这一规则会永久污染该幂等 key。

Follower 的职责与 Healing（修复）

Follower 永远不会直接执行领域写入，它们只是观察者。当发现已有幂等记录时：

• Succeeded → 返回缓存结果
• Pending → 查询领域表
• Failed → 拒绝请求

其中最关键的是 Pending 情况。

因为数据库才是最终真相（source of truth），follower 可以：

• 检查群组是否实际已经创建
• 将幂等记录“修复”为 succeeded
• 即使 leader 崩溃，也能返回正确结果

这使系统对以下情况具备韧性：

• 进程崩溃
• 网络失败
• 部分执行中断

为什么允许 Pending 泄漏

一个刻意的设计选择是：Pending 记录不保证被清理。

如果：

• leader 崩溃
• follower 没有成功修复
• 客户端最终放弃

那么该幂等记录可能永远停留在 Pending。

这是可以接受的，因为：

• Pending 不会阻塞新的幂等 key
• 不会产生重复领域状态
• 不影响其他无关请求

在本系统中，幂等记录是 best-effort 元数据，而不是关键基础设施。

将 Failed 视为终态

另一个刻意简化是：Failed 被视为 不可重试（non-retryable）。一旦 attempt 被标记为失败：

• 相同 key 永远失败
• 客户端必须生成新的幂等 key 才能重试

这种选择牺牲了一些灵活性，换来更强的清晰性：

• key 标识 attempt，而不是 intention
• 重试行为显式由客户端控制

避免复杂状态转换，同时保持安全。

保证与非保证（Guarantees and Non-guarantees）

该幂等设计保证：

• 每个幂等 key 最多创建一个群组
• 已提交的群组一定能被重试发现
• 并发执行最终收敛为单一结果

它不保证：

• 幂等元数据最终一定被清理
• 失败 attempt 可以用相同 key 重试
• 所有失败都能自动恢复

这些取舍是刻意且明确记录的。

为什么它与系统整体一致

该幂等模型与前文设计天然契合：

• at-least-once 事件发布（Outbox fanout）
• best-effort 实时投递（SessionHub actor）
• 领域状态作为 source-of-truth

通过将重试视为常态，将重复视为必然，系统在不引入过度复杂性的情况下保持正确。

结语

通过显式建模 attempt ownership、将元数据与领域真相分离，并定义清晰终态，系统在无需全局协调或后台修复进程的前提下，实现了故障条件下的正确性。

至此，聊天服务器的设计叙事闭环完成：

从结构 → 流程 → 并发 → 可靠性 → 最终到正确性。

文章目录

聊天服务器设计：架构、核心流程与可靠性保证