用于不相交集合的数据结构（并查集）（上 操作与实现）

一、并查集的操作

不相交集合之间可能有这些操作

1. MAKE-SET(x):建立一个新的集合，它的唯一成员是x（作为代表）。因为各个集合是不相交的，故x不会出现在别的某个集合中。
2. UNION(x, y):将包含x和y的两个集合合并为一个集合。
3. FIND-SET(x):返回一个指针，这个指针指向包含x的唯一的集合代表。

二、并查集的实现

1. 用链表表示并查集

可以用这样一个链表表示并查集。
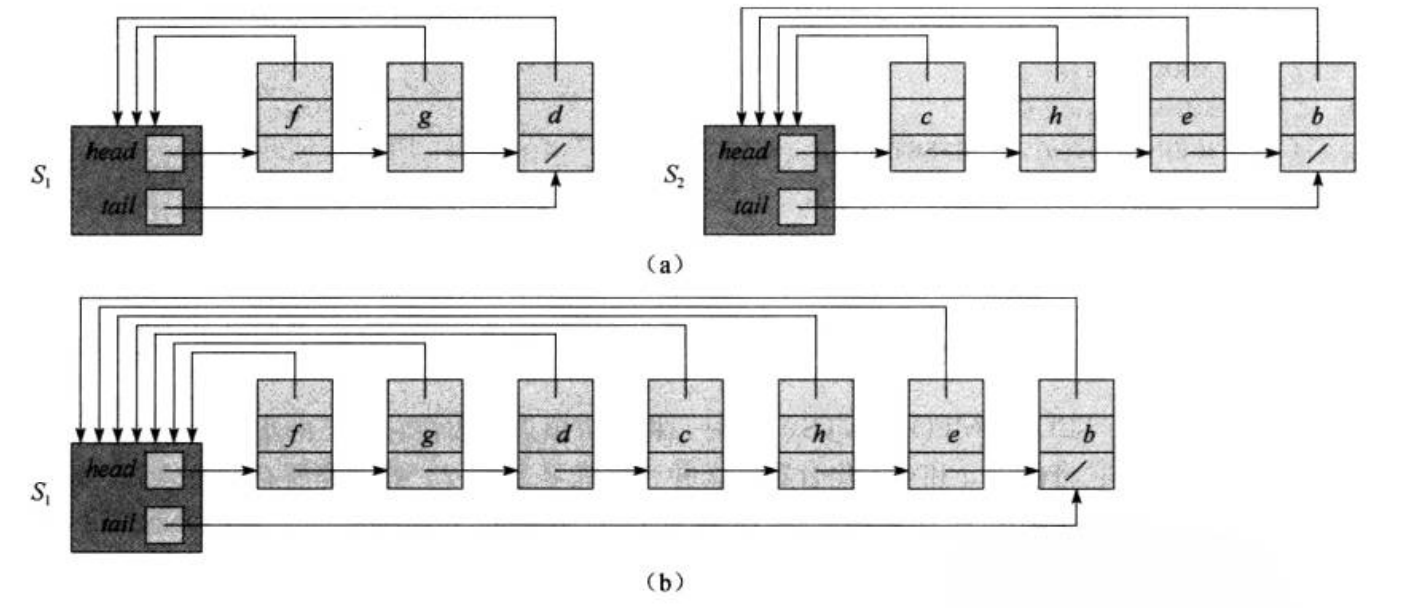
它含有一个头节点，头节点含有一个head指针和一个tail指针，分别指向队列的队首和队尾，队列中的每个节点都含有两个指针，一个指向头节点，一个指向队列中的下一个节点。显然，由这样的队列构成的并查集MAKE-SET(x)和FIND-SET(x)操作的时间复杂度都是O(1)，MAKE-SET(x)操作就是创建一个新的链表，FIND-SET(x)操作的时间复杂度就是返回x所在节点指向的头节点，它的时间复杂度也是O(1)。而UNION(x,y)的时间复杂度是O(n)，这是因为虽然拼接两个链表需要的操作数与n无关，但是被合并的集合中的每一个指向头节点的指针都需要改成指向新的头节点，这样可以看出用链表表示的并查集的UNION(x,y)操作时间复杂度为O(n)，其中n为被合并的集合的大小。

2. 不相交集合森林

如果用树表示单个集合，那么并查集就组成一个森林。用树表示并查集更简洁，它的每个节点都只有一个指向父节点的指针，最终指向根节点，根节点的父指针指向自己。这样FIND-SET(x)操作只需要找到根节点，就可以确认在哪个集合，那么这个集合最好的状态就是每一个节点的父指针都指向根节点。如下图

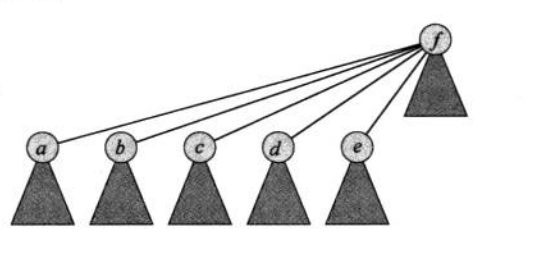
这种集合在进行UNION(x,y)操作时只需将一个集合的根的父指针指向另一个集合的根的父指针。

运行时间的改进

如上面所述，只有在一个集合中所有节点的父指针都指向根节点的时候集合的所有操作时间复杂度才为O(1)，否则时间复杂度与合并后的集合结构有关。

假设我们有这样一个集合：

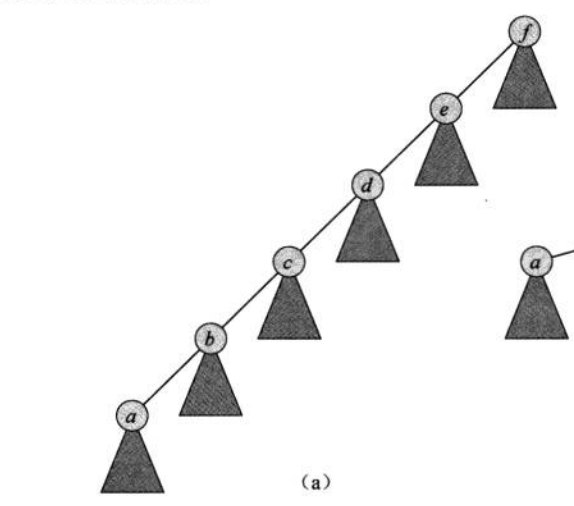
这是最坏情况，FIND-SET(x)操作需要遍历整个集合，合并a所在的集合也需要遍历整个集合。
为了降低各个操作时间复杂度，这里有两种启发策略：

1. 按秩合并：很容易想到的是使较少节点的树的根节点指向较多节点的树的根，具体做法是给每个节点维护一个秩，用于记录该节点高度的上界。这样，就可以在UNION(x,y)操作中将较小树节点的根指向较大树节点的根。
2. 路径压缩：在FIND-SET(x)操作中将遍历到的每个节点的父指针指向根节点，这样这些节点的后续操作次数都是常数。

下面是实现了按秩合并 路径压缩两种启发策略的代码：

import java.util.HashMap;
import java.util.List;

public class UnionFind {

	public static class Node {
		// whatever you like
	}

	public static class UnionFindSet {
		public HashMap<Node, Node> fatherMap;
		public HashMap<Node, Integer> sizeMap;

		public UnionFindSet() {
			fatherMap = new HashMap<Node, Node>();
			sizeMap = new HashMap<Node, Integer>();
		}

		public void makeSets(List<Node> nodes) { // 这里为了快速使用，采用List快速构造一个集合森林
			fatherMap.clear();
			sizeMap.clear();
			for (Node node : nodes) {
				fatherMap.put(node, node);
				sizeMap.put(node, 1);
			}
		}

		private Node findHead(Node node) {
			Node father = fatherMap.get(node);
			if (father != node) {
				father = findHead(father);
			}
			fatherMap.put(node, father);// 合并操作中将父指针指向根节点
			return father;
		}
		
		public boolean isSameSet(Node a, Node b) {
			return findHead(a) == findHead(b);
		}

		public void union(Node a, Node b) {
			if (a == null || b == null) {
				return;
			}
			Node aHead = findHead(a);
			Node bHead = findHead(b);
			if (aHead != bHead) {
				int aSetSize= sizeMap.get(aHead);
				int bSetSize = sizeMap.get(bHead);
				if (aSetSize <= bSetSize) {
					fatherMap.put(aHead, bHead);
					sizeMap.put(bHead, aSetSize + bSetSize);
				} else {
					fatherMap.put(bHead, aHead);
					sizeMap.put(aHead, aSetSize + bSetSize);
				}
			}
		}

	}
}

关于带路径压缩的按秩合并时间复杂度分析可以参考《算法导论 第三版》p331-335，有5页数学证明，这里不详述。