手撕排序算法
排序
大多数人学习编程语言学到循环的时候,接触到的第一个算法可能就是排序吧。所以关于数据结构与算法的第一篇博客从排序开始写起。
首先是三种时间复杂度为O(N²)的排序算法
一、选择排序
选择排序是最容易理解的排序算法,在待排序的顺序表中,每次都从未排好序的区域中找到最小值,放到排好序的后面,直到所有顺序都排好。
public static void selectSort(int[] arr) {
if(arr == null) return;
for (int i = 0; i < arr.length; i++) {
for (int j = i; j < arr.length; j++) {
if (arr[j] < arr[i]) {
swap(arr, i, j);
}
}
}
}
private static void swap(int[] arr, int x, int y) {
int temp = arr[x];
arr[x] = arr[y];
arr[y] = temp;
}
二、冒泡排序
冒泡排序的思路非常容易,依次向后比较相邻的两个值,将大值放后面,这样值就像气泡一样,最大的最先冒出水面,这样每次都把最大的值放到未排好序的位置之后,就可以依次排好顺序了。
public static void bubbleSort(int[] arr) {
if (arr == null) return;
for (int i = arr.length; i > 0; i--) {
for (int j = 0; j < i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
}
}
}
}
private static void swap(int[] arr, int x, int y) {
int temp = arr[x];
arr[x] = arr[y];
arr[y] = temp;
}
三、插入排序
插入排序思路就像我们打扑克牌时理牌的过程,我们每拿起一张新牌,都将它插入到原来排好序的顺序表中,直到拿完所有的牌就排好了序,反应到程序中,就是每次都从未排好序的序列中拿出一个值与前面的值进行比较,直到插入到合适的位置。
public static void insertSort(int[] arr) {
if (arr == null) return;
for (int i = 1; i < arr.length; i++) {
for (int j = i; j > 0; j--) {
if (arr[j] < arr[j - 1]) {
++count;
swap(arr, j, j - 1);
} else {
break;
}
}
}
}
private static void swap(int[] arr, int x, int y) {
int temp = arr[x];
arr[x] = arr[y];
arr[y] = temp;
}
四、希尔排序
希尔排序是在插入排序的基础上改进出来的排序算法。它不再将每个数单独插入,而是分组插入。首先 将待排序的数组平均分成两组,将第二组与第一组对应的数进行比较
假如有这样一个序列
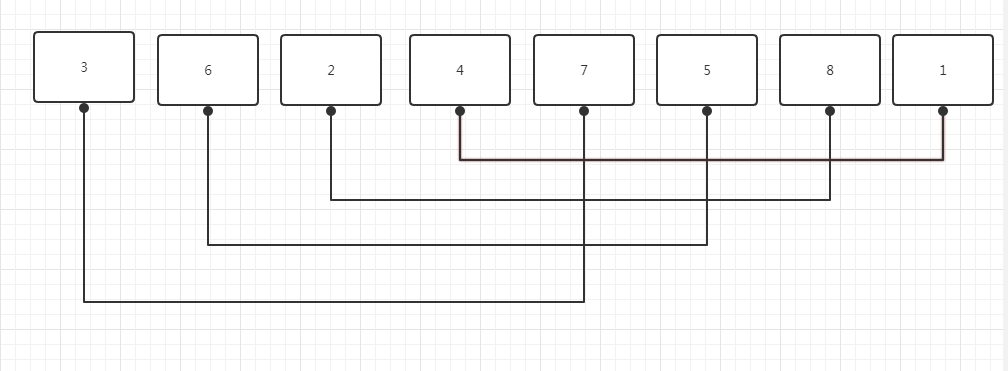
第一步 前4个一组 后4个一组 然后将两组的数一一对应,将顺序不对的位置进行交换
交换之后的结果是这样:

第二步 继续将序列分为2² = 4 组,然后按类似插入排序的方式每组按第一步的形式插入
后面依次分为 8 16 32 ...... 直到每组只有一个数据,进行一轮插入,就完成了排序
反应到代码如下:
public static void shellSort(int[] arr) {
for (int r = arr.length / 2; r > 0; r /= 2) {
for (int i = r; i < arr.length; i++) {
for (int j = i - r; j >= 0; j -= r) {
if (arr[j] > arr[j + r]) {
swap(arr, j, j + r);
} else break;
}
}
}
}
private static void swap(int[] arr, int x, int y) {
int temp = arr[x];
arr[x] = arr[y];
arr[y] = temp;
}
五、归并排序
1.我们需要理解这样一个过程:
假如有两个已经排好序的序列,我们将他们合并成一个新的有序序列,应该怎么做?
比如
1 2 4 7 和 3 5 6 8
很简单 两个下标指针指向两个序列的头,谁小谁就填入新数组,并且指针向后移动,当其中一个指针到达最后时,再将另一个数组剩余的数全部填入新数组。
2.有了上述方法,再想到每个只有一个元素的数组都是已经排号序的数组,那么可以想到,无论多长的序列都是由单元素数组组成的,并且合并之后的数组还是有序的,那么只需递归的执行这个合并的过程,最后得到的数组也是有序的。
归并排序代码如下:
public static void mergeSort(int[] arr) {
if (arr == null || arr.length < 1) return;
help = new int[arr.length];
mergeSort(arr, 0, arr.length - 1);
}
public static void mergeSort(int[] arr, int l, int r) {
if (r == l) return;
int mid = l + ((r - l) >> 1);
mergeSort(arr, l, mid);
mergeSort(arr, mid + 1, r);
merge(arr, l, mid, r);
}
private static void merge(int[] arr, int l, int mid, int r) {
int cur1 = l, cur2 = mid + 1;
int i = l;
while (cur1 <= mid && cur2 <= r) {
help[i++] = arr[cur1] < arr[cur2] ? arr[cur1++] : arr[cur2++];
}
while (cur1 <= mid) {
help[i++] = arr[cur1++];
}
while (cur2 <= r) {
help[i++] = arr[cur2++];
}
for (int j = l; j <= r; j++) {
arr[j] = help[j];
}
}
六、堆排序
-
堆排序需要理解堆结构,通常我们所说的大根堆就是一个完全二叉树,它的任意一个子树的根都是最大值。通过大根堆这个结构可以很快找到最大值,然后我们将整个堆的跟交换到已排号序的序列前面,然后将前面的堆继续调整为大根堆,以此类推,就可以将整个序列排好序。
-
然后我们需要知道如何构建一个堆,这里的堆是一个逻辑结构,没必要在内存中构建一个树形结构,而是通过数组下标表示。假设某个节点下标是index,那么它的父节点下标是(index - 1) / 2。那么我们构建一个堆的方式就是每加入一个元素,就与父节点进行比较。如果父节点小于新插入节点,就交换本节点与父节点位置,直到该节点小于父节点或者成为根节点。
-
还需要理解的是,根节点被替换后,如何将其重新调整为一个大根堆。当根节点被替换后,需要跟子节点的最大值比较,如果本节点小于子节点最大值,就需要与最大值节点交换,直到该节点到合适位置。
理解上面3点之后就可以理解堆排序的流程了
下面是代码:
public static void heapSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
heapInsert(arr, i);
}
for (int i = arr.length - 1; i > 0; i--) {
swap(arr, i, 0);
heapIfy(arr, i);
}
}
private static void heapIfy(int[] arr, int heapSize) {
int i = 0;
int p;
int left = i * 2 + 1;
while (left < heapSize) {
int right = left + 1;
if (right < heapSize) {
p = arr[left] > arr[right] ? left : right;
} else {
p = left;
}
if (arr[i] < arr[p]) {
swap(arr, i, p);
i = p;
left = i * 2 + 1;
} else {
break;
}
}
}
private static void heapInsert(int[] arr, int index) {
while (arr[index] > arr[(index - 1) / 2]) {
swap(arr, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
private static void swap(int[] arr, int x, int y) {
int temp = arr[x];
arr[x] = arr[y];
arr[y] = temp;
}
七、快速排序
- 在理解快速排序之前需要理解一个荷兰国旗问题:就是从数组中随机抽取一个数(称之为轴),并将数组划分为 小于该数,等于该数,大于该数 三个部分
首先 随机抽取一个数,设定less作为小于区域的指针位于-1位置,more作为大于区域指针位于length区域位置。
然后扫描数组,遇到小于轴的数时,与++less交换,并继续扫描下一个;遇到等于轴的数时,继续扫描下一个;遇到大于轴的数时,则与--more交换,并继续扫描当前数。直到扫描下标与more相遇则完成了划分。
2.与归并排序相似,将大问题拆分成小问题,每次将待排序区域划分为荷兰国旗形式,直到待划分区域只有一个数,则完成了排序。
代码如下:
public static void quickSort(int[] arr) {
if(arr == null) return;
quickSort(arr, 0, arr.length - 1);
}
private static void quickSort(int[] arr, int l, int r) {
if (r > l) {
int[] partition = partition(arr, l, r);
quickSort(arr, l, partition[0]);
quickSort(arr, partition[1], r);
}
}
private static int[] partition(int[] arr, int l, int r) {
int pivot = arr[(int) ((Math.random() * (r - l)) + l)];
int less = l - 1;
int more = r + 1;
int i = l;
while (i < more) {
if (arr[i] < pivot) {
swap(arr, ++less, i++);
} else if (arr[i] > pivot) {
swap(arr, --more, i);
} else {
++i;
}
}
return new int[]{less, more};
}
private static void swap(int[] arr, int x, int y) {
int temp = arr[x];
arr[x] = arr[y];
arr[y] = temp;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号