首先，我们需要明确矩阵是一个数表，行列式是数表所确定的一个数，所以行列式可以看作是矩阵的函数，行列式也是矩阵划分奇异矩阵和非奇异矩阵的标志。
        矩阵的逆的引入有多种角度，按书中如果同型矩阵AB=E那么他们他们互为逆矩阵，如果一个方阵其行列式不等于零，那么这个方阵可逆等等，从表面上看讲不出它们之间的联系，我们会在以后矩阵的初等变换中有深入的理解。下面我不加证明的列出一些常用结论，我会在学习中继续总结补充并更新。
1、如果A是可逆矩阵，那么包括对称性，可逆性，正交性等矩阵的重要性质A与A*同时具有或同时不具有，即互为充要条件。
2、如果N阶方阵A、B及A+B均可逆则   可以逆且等于

3、对于分块巨阵求逆，有以下结论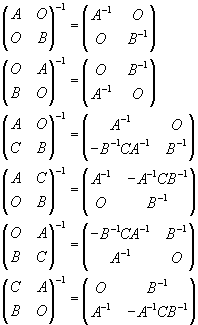


同时我们加上这个求伴随分块矩阵的这个结论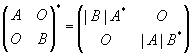

对于矩阵的幂的运算有如下结论


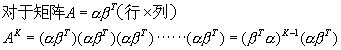
以上没有列出有关矩阵的逆的简单公式，这些仅是学习中的总结我会及时补充发现的新结论，如需要证明过程的网友，请给我留言
补充：
1.R(A)=R(A^T);
2.R(A)+R(B)<=R(A+B)
3.R(AB)=MIN(R(A),R(B))
4.如果A可逆，则R(AB)=R(B);如果B可逆，则R(AB)=R(A)
5.A是m*n矩阵，b是n*p阶矩阵，如果AB=0那么R(A)+R(B)<=N
6.设A是N阶方阵（N>2），那么
R(A*)=N，当R(A)=N;
R(A*)=1,当R(A)=N-1；
R(A*)=0；当R(A)<=N-1；
对于2。
AB矩阵是由A的行和B的列决定的，它的稚也限制于A的行和B的列即R(AB)小于等于AB行和列中最少的那个
而A,B行列最少那个同时也是R(A),R(B)的制约条件，当等号成立时即m*n阶A和n*p阶B中的n比m和p都小
对于4
对AB实行初等变换后的稚与AB的稚相同而乘以A.B的逆就相当于对AB实行初等变换。
对于5
AB=0可以看成是奇次方程组A(b1,b2,b3...)
设R(A)=r, R(B)=t;那么A有n-r个自由变量所以B中每个向量都可以用这n-r个自由变量线性表示由（李永乐书    P391定理3.10）得T<=N-R所以...