YOLOv11改进大全：卷积层、轻量化、注意力机制、损失函数、Backbone、SPPF、Neck、检测头全方位优化汇总

前言

本文介绍了 DiffCLIP，一种将差分注意力机制集成到 CLIP 架构的视觉 - 语言模型，并将其应用于 YOLOv11。差分注意力机制通过计算两个互补注意力分布的差值，抵消无关信息干扰。单头差分注意力将 Q 和 K 拆分，分别计算注意力分布后做差值融合；多头差分注意力则每个头独立执行差分操作后聚合输出。关键参数 λ 可动态调控噪声抵消强度。我们将 DiffAttention 代码集成到 YOLOv11 中，替换原有模块。实验表明，改进后的 YOLOv11 在图像 - 文本理解任务中表现出色。

文章目录： YOLOv11改进大全：卷积层、轻量化、注意力机制、损失函数、Backbone、SPPF、Neck、检测头全方位优化汇总

专栏链接: YOLOv11改进专栏

介绍

摘要

我们提出DiffCLIP，一种新颖的视觉-语言模型，它将差分注意力机制扩展到CLIP架构中。差分注意力机制最初是为大型语言模型开发的，用于放大相关上下文同时消除噪声信息。在本研究中，我们将这一机制整合到CLIP的双编码器（图像和文本）框架中。通过引入少量额外参数，DiffCLIP在图像-文本理解任务上取得了卓越的性能。在零样本分类、检索和鲁棒性基准测试中，DiffCLIP始终优于基准CLIP模型。值得注意的是，这些改进几乎不增加计算开销，表明差分注意力机制可以显著增强多模态表征而不牺牲效率。代码可在https://github.com/hammoudhasan/DiffCLIP获取。

文章链接

论文地址：论文地址

代码地址：代码地址

基本原理

DiffAttention（差分注意力）是一种针对传统Transformer注意力机制“注意力噪声”问题提出的改进方案，核心思路是通过两个互补注意力分布的差值计算，抵消无关信息干扰，强化对关键特征的聚焦。其技术原理可从核心设计理念、单头/多头实现细节、参数调控机制及与传统注意力的差异四个维度展开，同时结合跨领域应用逻辑（如语言模型、图文模型）进行完整解析。

单头差分注意力（Single-Head DiffAttention）：基础实现单元

单头DiffAttention是DiffAttention的核心模块，通过“拆分Q/K→双Softmax计算→差值融合”三步，实现噪声抵消。具体流程如下：

步骤1：拆分Q和K为两组互补子空间

将传统注意力中的查询（Q）和键（K）沿特征维度（$d$）均分为两组，形成两个独立的子空间，用于捕捉不同类型的注意力信号（一组侧重关键信息，一组侧重噪声）：

• 设输入序列$X \in \mathbb{R}^{N \times d}$，生成Q和K后，拆分得到：
  $Q_1, Q_2 \in \mathbb{R}^{N \times \frac{d}{2}}$（Q的两组子查询），$K_1, K_2 \in \mathbb{R}^{N \times \frac{d}{2}}$（K的两组子键）；
• 值（V）不拆分，仍为$V \in \mathbb{R}^{N \times d}$，确保输出特征维度与输入一致。

步骤2：分别计算两组注意力分布（双Softmax）

对两组子Q和子K，分别计算独立的注意力权重矩阵$A_1$ 和$A_2$，模拟“信号”和“噪声”两种分布：

• 第一组注意力（侧重关键信号）：$A_1 = softmax\left( \frac{Q_1 K_1^\top}{\sqrt{\frac{d}{2}}} \right)$；
• 第二组注意力（侧重噪声）：$A_2 = softmax\left( \frac{Q_2 K_2^\top}{\sqrt{\frac{d}{2}}} \right)$；
• 分母$\sqrt{\frac{d}{2}}$ 是对拆分后子空间维度的缩放，避免因维度减半导致注意力分数过大（与传统注意力的“$\sqrt{d}$”缩放逻辑一致，保证数值稳定性）。

步骤3：差值融合与加权输出（核心“差分”操作）

通过可学习参数$\lambda$ 平衡两组注意力的贡献，用$A_1$ 减去“$\lambda$ 缩放后的$A_2$”，抵消噪声并保留关键信号，最终与V加权得到输出：

1. 差分注意力权重计算：$A_{diff} = A_1 - \lambda \cdot A_2$；
2. 加权输出：$DiffAttn(X) = A_{diff} \cdot V$。

关键逻辑：$A_1$ 和$A_2$ 中对“无关token”的注意力权重（噪声）具有较强的一致性，相减后会相互抵消；而对“关键token”的注意力权重（信号）在两组中差异较大，会被保留甚至强化，最终形成更稀疏、聚焦的注意力分布（如图2中DiffCLIP对“杯子”“花朵”的聚焦，相比CLIP避免了背景干扰）。

3. 多头差分注意力（Multi-Head DiffAttention）：工程化扩展

为捕捉多维度的特征依赖（如文本中的语法依赖、语义依赖，图像中的局部纹理、全局结构），DiffAttention需扩展为多头形式（类似传统Transformer的Multi-Head Attention），核心是“每个头独立执行差分操作，最后聚合输出”。具体流程如下：

步骤1：多头拆分与独立差分计算

设多头数量为$h$，将输入特征维度$d$ 拆分为$h$ 个小头维度$d_h = \frac{d}{h}$，每个头$i$ 独立执行单头DiffAttention：

• 对第$i$ 个头，拆分Q/K为两组子空间：$Q_{1,i}, Q_{2,i} \in \mathbb{R}^{N \times \frac{d_h}{2}}$，$K_{1,i}, K_{2,i} \in \mathbb{R}^{N \times \frac{d_h}{2}}$；
• 计算该头的差分注意力权重：$A_{diff,i} = softmax\left( \frac{Q_{1,i} K_{1,i}^\top}{\sqrt{\frac{d_h}{2}}} \right) - \lambda_i \cdot softmax\left( \frac{Q_{2,i} K_{2,i}^\top}{\sqrt{\frac{d_h}{2}}} \right)$；
• 该头输出：$DiffAttn_i(X) = A_{diff,i} \cdot V_i$（$V_i \in \mathbb{R}^{N \times d_h}$ 为第$i$ 头的子值）。

步骤2：多头输出聚合

将$h$ 个小头的输出沿特征维度拼接，再通过一个线性投影层（$W^O \in \mathbb{R}^{h \cdot d_h \times d}$）恢复为原输入维度，得到最终多头DiffAttention输出：
$DiffMHA(X) = \left[ DiffAttn_1(X) \parallel DiffAttn_2(X) \parallel \dots \parallel DiffAttn_h(X) \right] \cdot W^O$。

优势：每个头可捕捉不同类型的关键特征（如文本头1关注语法结构、头2关注语义关联），通过独立差分操作分别降噪，聚合后能更全面地保留有用信息，进一步提升模型对复杂依赖的建模能力。

4. 关键参数$\lambda$：动态调控噪声抵消强度

参数$\lambda$ 是DiffAttention的核心调控因子，用于平衡“信号保留”和“噪声抵消”的强度，其取值直接影响差分注意力的效果。根据论文（Ye et al., 2024; Hammoud et al., 2025），$\lambda$ 的设计遵循以下原则：

（1）$\lambda$ 的计算方式：动态学习而非固定

$\lambda$ 并非人工设定的超参数，而是通过模型训练动态学习，具体公式为：
$\lambda = exp(\lambda_{q1} \cdot \lambda_{k1}) - exp(\lambda_{q2} \cdot \lambda_{k2}) + \lambda_{init}$
-$\lambda_{q1}, \lambda_{k1}, \lambda_{q2}, \lambda_{k2}$：可学习权重，分别与两组Q/K的子空间关联，用于适配不同任务中Q/K的特征分布；
-$\lambda_{init}$：初始超参数（如DiffCLIP中设为0.8），为训练提供稳定初始值，避免初期差分过度导致信号丢失。

（2）$\lambda$ 的作用逻辑

• 当$\lambda$ 较大时：$A_2$ 的权重被强化，噪声抵消更彻底，但可能误删部分弱关键信号（如长文本中的次要逻辑词）；
• 当$\lambda$ 较小时：$A_2$ 的权重被削弱，噪声抵消不充分，但能保留更多潜在关键信息；
• 训练过程中，模型会根据任务需求（如文本生成需保留语法信号、图文检索需保留视觉物体信号）自适应调整$\lambda$，实现“降噪”与“信号保留”的平衡。

核心代码

class DiffAttention(nn.Module):
r"""
Differential Attention Module.

Given an input tensor X ∈ ℝ^(B×N×d_model), we first compute the linear projections:

Q = X Wᵠ, K = X Wᵏ, V = X Wᵛ

The queries and keys are then reshaped and split into two parts:
Q → [Q₁; Q₂] ∈ ℝ^(B, N, 2·h_effective, d_head)
K → [K₁; K₂] ∈ ℝ^(B, N, 2·h_effective, d_head)
with h_effective = num_heads // 2 and d_head = d_model / num_heads.

The value projection is reshaped to:
V ∈ ℝ^(B, N, h_effective, 2·d_head)

We then compute two attention maps:
A₁ = softmax((Q₁ K₁ᵀ) / √d_head)
A₂ = softmax((Q₂ K₂ᵀ) / √d_head)

A learnable scalar λ is computed via:
λ = exp(λ_{q1} ⋅ λ_{k1}) − exp(λ_{q2} ⋅ λ_{k2}) + λ_init

Finally, the differential attention output is:
DiffAttn(X) = (A₁ − λ · A₂) · V

The per-head outputs are then normalized headwise with RMSNorm and projected back to d_model.

Args:
dim (int): Embedding dimension (d_model).
num_heads (int): Number of heads in the original transformer (must be even).
qkv_bias (bool): If True, add a bias term to the Q, K, V projections.
attn_drop (float): Dropout probability after softmax.
proj_drop (float): Dropout probability after the output projection.
lambda_init (float): Initial constant for lambda re-parameterization.
"""
def __init__(self, dim, num_heads=8, qkv_bias=True, attn_drop=0., proj_drop=0., lambda_init=0.8):
super().__init__()
if num_heads % 2 != 0:
raise ValueError("num_heads must be even for Differential Attention.")
self.dim = dim
self.num_heads = num_heads # original number of heads
self.effective_heads = num_heads // 2 # differential attention operates on half as many heads
self.head_dim = dim // num_heads # per-head dimension
self.scaling = self.head_dim ** -0.5

# Linear projections for Q, K, V: mapping from dim → dim.
self.q_proj = nn.Linear(dim, dim, bias=qkv_bias)
self.k_proj = nn.Linear(dim, dim, bias=qkv_bias)
self.v_proj = nn.Linear(dim, dim, bias=qkv_bias)
self.out_proj = nn.Linear(dim, dim, bias=True) # final output projection

self.attn_drop = nn.Dropout(attn_drop)
self.proj_drop = nn.Dropout(proj_drop)

# RMSNorm for headwise normalization on outputs (each head's output has dimension 2·head_dim)
self.diff_norm = RMSNorm(2 * self.head_dim, eps=1e-5, elementwise_affine=True)

# Learnable lambda parameters (shared across all heads)
self.lambda_q1 = nn.Parameter(torch.zeros(self.head_dim, dtype=torch.float32).normal_(mean=0, std=0.1))
self.lambda_k1 = nn.Parameter(torch.zeros(self.head_dim, dtype=torch.float32).normal_(mean=0, std=0.1))
self.lambda_q2 = nn.Parameter(torch.zeros(self.head_dim, dtype=torch.float32).normal_(mean=0, std=0.1))
self.lambda_k2 = nn.Parameter(torch.zeros(self.head_dim, dtype=torch.float32).normal_(mean=0, std=0.1))
self.lambda_init = lambda_init

def forward(self, x: torch.Tensor) -> torch.Tensor:
"""
Args:
x (Tensor): Input tensor of shape (B, N, d_model).

Returns:
Tensor of shape (B, N, d_model) after applying differential attention.
"""
B, N, _ = x.shape

# Compute Q, K, V projections.
q = self.q_proj(x) # shape: (B, N, d_model)
k = self.k_proj(x) # shape: (B, N, d_model)
v = self.v_proj(x) # shape: (B, N, d_model)

# Reshape Q and K into (B, N, 2 * h_effective, head_dim)
q = q.view(B, N, 2 * self.effective_heads, self.head_dim)
k = k.view(B, N, 2 * self.effective_heads, self.head_dim)
# Reshape V into (B, N, h_effective, 2 * head_dim)
v = v.view(B, N, self.effective_heads, 2 * self.head_dim)

# Transpose to bring head dimension forward.
# q, k: (B, 2 * h_effective, N, head_dim)
q = q.transpose(1, 2)
k = k.transpose(1, 2)
# v: (B, h_effective, N, 2 * head_dim)
v = v.transpose(1, 2)

# Scale Q.
q = q * self.scaling

# Compute raw attention scores: (B, 2 * h_effective, N, N)
attn_scores = torch.matmul(q, k.transpose(-1, -2))

# Compute attention probabilities.
attn_probs = F.softmax(attn_scores, dim=-1)
attn_probs = self.attn_drop(attn_probs)

# Reshape to separate the two halves: (B, h_effective, 2, N, N)
attn_probs = attn_probs.view(B, self.effective_heads, 2, N, N)

# Compute lambda via re-parameterization.
lambda_1 = torch.exp(torch.sum(self.lambda_q1 * self.lambda_k1))
lambda_2 = torch.exp(torch.sum(self.lambda_q2 * self.lambda_k2))
lambda_full = lambda_1 - lambda_2 + self.lambda_init

# Differential attention: subtract the second attention map scaled by lambda_full.
diff_attn = attn_probs[:, :, 0, :, :] - lambda_full * attn_probs[:, :, 1, :, :] # shape: (B, h_effective, N, N)

# Multiply the differential attention weights with V.
attn_output = torch.matmul(diff_attn, v) # shape: (B, h_effective, N, 2 * head_dim)

# Apply RMSNorm (headwise normalization) and scale by (1 - lambda_init)
attn_output = self.diff_norm(attn_output) * (1 - self.lambda_init)

# Concatenate heads: reshape from (B, h_effective, N, 2 * head_dim) → (B, N, 2 * h_effective * head_dim)
attn_output = attn_output.transpose(1, 2).reshape(B, N, 2 * self.effective_heads * self.head_dim)

# Final linear projection.
x_out = self.out_proj(attn_output)
x_out = self.proj_drop(x_out)
return x_out

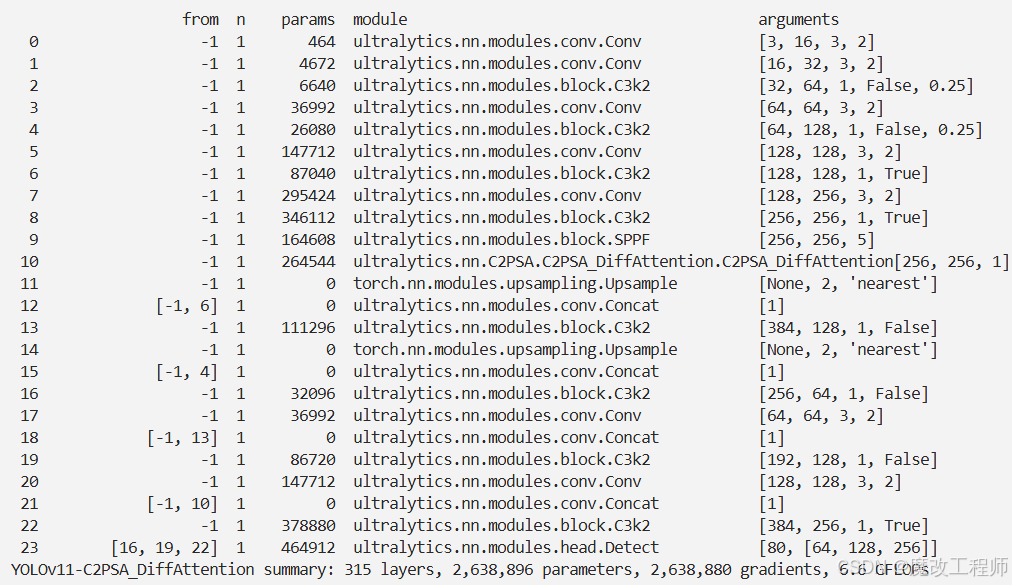
结果