无向图的割点与桥
无向图的割点与桥
写在前面:割边和割点都是对于无向图而言的
给定无向连通图\(G=(V,E)\),
若对于\(x\)属于\(V\),从图中删去节点\(x\)以及所有和\(x\)关联的边之后,G分裂成两个或者两个以上的不相连的子图,则称\(x\)是\(G\)的割点
若对于\(e\)属于\(E\)从图中边\(e\)后,\(G\)分裂成两个不相连的子图,则称\(e\)是\(G\)的桥或割边
\(tarjan\)基于无向图的深度优先遍历
引入时间戳这个概念
时间戳
在图的深度优先搜索中,按照每个节点第一次访问的时间顺序,一次给予\(N\)个节点\(1~N\)的整数标记,记为\(dfn[i]\)
搜索树
在无向图联通图中,任意选择一个节点出发进行深度优先遍历,每个点只访问一次,所有发生递归的边\((x,y)\)构成一棵树,我们把它称为无向连通图的搜索树。当然,一般无向图(不一定联通)的各个连通块的搜索树构成无向图的搜索森林
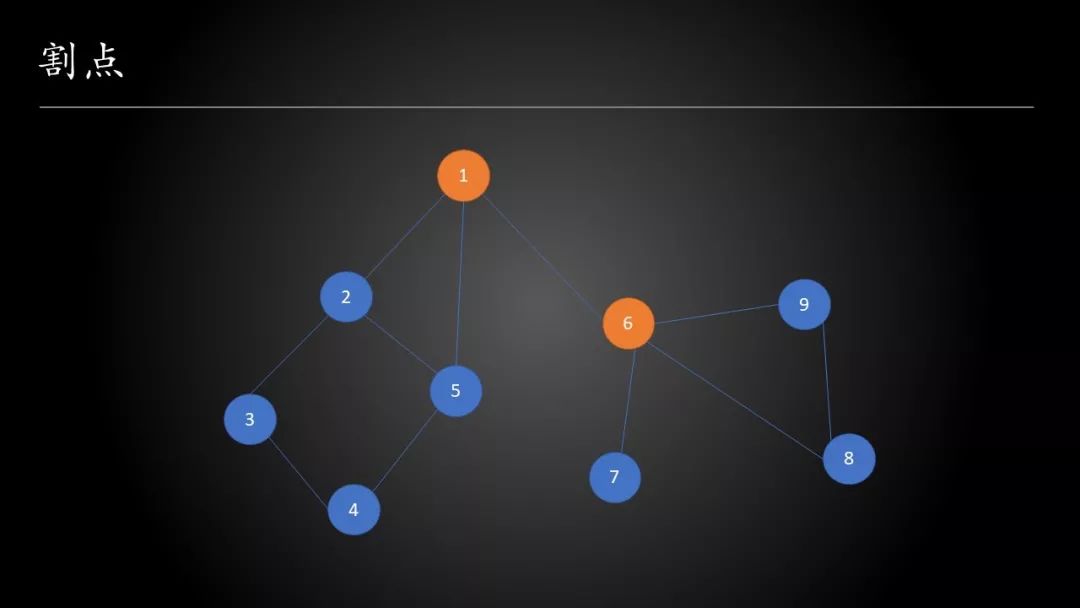
下图是一张无向连通图,图中的节点标明了时间戳
追溯值
除了时间戳之外,\(tarjan\)算法还引入了一个追溯值\(low[i]\),设\(subtree(x)\)表示搜索树中以\(x\)为根的子树
\(low[x]\)定义为以下节点的时间戳的最小值
- \(subtree(x)\)中的节点
- 通过一条不在搜索树上的边,能够达到\(subtree(x)\)的节点
比如在上面的这张图中,为了叙述方便,我们用时间戳来代表节点的编号,subtree(2)={2,3,4,5}
另外,1号节点可以通过\((1,5)\)这条不在搜索树上的边到达subtree(2),所以\(low[2]=1\)
根据定义,为了计算\(low[x]\),应该先令\(low[x]=dfn[x]\),然后考虑从\(x\)出发的每条边\((x,y)\)
若在搜索树上\(x\)是\(y\)的父节点,则令\(low[x]=min(low[x],low[y])\)
若无向边\((x,y)\)不是搜索树上的边,则令\(low[x]=min(low[x],dfn[x])\),对应上图的边\((1,5)\)
下图中的中括号[ ]里的数值,标明了每个节点的追溯值\(low[ \ ]\)

割边判定法则
无向边\((x,y)\)是桥,当且仅当搜索树上存在\(x\)的一个子节点\(y\)满足:
\(dfn[x]<low[y]\)
根据定义,\(dfn[x]<low[y]\)说明从\(subtree(y)\)出发,在不经过\((x,y)\)前提下,不管走哪一条边,都无法到达\(x\)或者比\(x\)更早访问的节点,若把\((x,y)\)删除,则\(subtree(y)\)好像构成了一个封闭的环境,与节点\(x\)没有边相连,图断开成为了两部分,因此\((x,y)\)是割边
反之,若不存在这样的节点\(y\),使得\(dfn[x]<low[y]\),则说明每个\(subtree(y)\)都能够绕行其他边到达\(x\)后者比\(x\)更早访问的节点,\((x,y)\)自然就不是割边
下面的无向图中有两条桥边,用虚线表示,红色表示递归边,不难发现,桥一定是搜索树种的边,并且一个简单环中的边一定都不是桥

下面的程序能求出一张无向图中中所有的桥,特别需要注意,因为我们遍历的是无向图,所以从每个点\(x\)出发,总能访问到它的父亲节点 \(fa\) ,根据\(low\)的计算方法,\((x,fa)\)属于搜索树上的边,且\(fa\)不是\(x\)的子节点,所以不能用 \(fa\) 的时间戳 \(dfn\) 来更新 \(low[x]\)
一个好的解决方案是:改为记录"递归进入每个节点的边的编号"编号可以认为是边在邻接表中存储的下标的位置。若沿着编号为\(i\)的边递归进入了节点\(x\),则忽略从\(x\)出发的编号为\(x \ xor \ 1\)的边,通过其他边计算\(low[x]\)即可
代码
#include<bits/stdc++.h>
using namespace std;
const int N=200000;
int ne[N],ver[N],head[N],idx;
int dfn[N],low[N];
bool bridge[N];
int timespace;
int n,m;
void add(int u,int v)
{
ne[idx]=head[u];
ver[idx]=v;
head[u]=idx;
idx++;
}
void tarjan(int x,int edge)
{
dfn[x]=low[x]=++timespace;
for(int i=head[x];i!=-1;i=ne[i])
{
int j=ver[i];
if(!dfn[j])
{
tarjan(j,i);//对应我们的搜索树中的边,也就是我们上面加粗的边,不断沿着它递归下去
low[x]=min(low[x],low[j]);//在回溯的时候进行更新,因为j是x的儿子节点,并且i这条边在搜索树上,所以我们用low[j]的值去更新low[x]的值
if(low[j]>dfn[x])//割边法则
bridge[i]=bridge[i^1]=1;//将其设为是割边
}
else if(i!=(edge^1))
{
low[x]=min(low[x],dfn[j]);
}
}
}
int main()
{
memset(head,-1,sizeof(head));
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int a,b;
cin>>a>>b;
add(a,b);
add(b,a);//加入无向边
}
for(int i=1;i<=n;i++)
{
if(!dfn[i])
tarjan(i,0);
}
for(int i=0;i<idx;i+=2)//因为我们加的是无向边,不同边的编号相差2
if(bridge[i])
{
printf("%d %d\n",ver[i],ver[i^1]);
}
return 0;
}
/*
8 11
1 2
1 5
2 5
2 3
3 4
4 5
1 6
6 7
6 9
8 9
6 8
*/
割点判定法则
若\(x\)不是搜索树的根节点(深度优先遍历的起点),则\(x\)是割点当且仅当搜索树上存在\(x\)的一个子节点\(y\)满足
\(dfn[x]<=low[y]\)
特别的,若\(x\)是搜索树的根节点,则\(x\)是割点,当且仅当搜索树上存在至少两个子节点满足上面的条件
证明:根据定义,\(dfn[x]<=low[y]\),说明\(y\)这个点不能回到自己的祖先节点,那么\(x\)为割点
因为割点的判定法则是小于等于号,所以我们并不用考虑父亲节点和重边的问题,从\(x\)出发能访问到的所有点的时间戳都可以用来更新\(low[x]\)
#include<bits/stdc++.h>
using namespace std;
const int N=200000;
int ne[N],ver[N],idx,head[N];
int dfn[N],low[N],timespace;
int n,m;
int cnt[N];
int root;
int tot;
void add(int u,int v)
{
ne[idx]=head[u];
ver[idx]=v;
head[u]=idx;
idx++;
}
void tarjan(int x)
{
dfn[x]=low[x]=++timespace;
int flag=0;
for(int i=head[x]; i!=-1; i=ne[i])
{
int j=ver[i];
if(!dfn[j])
{
tarjan(j);
low[x]=min(low[x],low[j]);
if(low[j]>=dfn[x])
{
flag++;
if(flag>1||x!=root)
{
cnt[x]=true;
}
}
}
else
{
low[x]=min(low[x],dfn[j]);
}
}
}
int main()
{
memset(head,-1,sizeof(head));
cin>>n>>m;
for(int i=1; i<=m; i++)
{
int a,b;
cin>>a>>b;
add(a,b);
add(b,a);
}
for(int i=1; i<=n; i++)
if(dfn[i]==0)
root=i,tarjan(i);
for(int i=1; i<=n; i++)
if(cnt[i]) tot++;
printf("%d\n",tot);
for(int i=1; i<=n; i++)
if(cnt[i])
printf("%d ",i);
return 0;
}
注意:这里我们在统计的时候,割点的个数不能放在tarjan里面去统计,因为如果在某个点时多次\(low[y]>=dfn[x]\),cnt会多次++,切记切记



 浙公网安备 33010602011771号
浙公网安备 33010602011771号