房屋积水

B3731 [信息与未来 2017] 房屋积水

题目描述

乌龟家的屋顶是凹凸不平的，所以每次雨后都会积水。为了知道屋顶是否会在暴雨后塌掉，他把屋顶的形状给了你，希望你帮他计算暴雨后屋顶的积水总量。

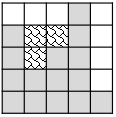
乌龟的屋顶由顺次排在同一水平线上的 \(n\) 个宽度为 \(1\)、高度为整数 (分别给出) 的瓦片组成。例如给定 \(n=5\)，瓦片的高度分别为 \(4,2,3,5,1\)，屋顶可以画在下图所示的网格中，灰色格子为瓦片。

暴雨过后，如果一个方格向左右两侧延伸都能到达瓦片占据的方格，它就会积水。所以图中波浪线格子在暴雨后会积水，屋顶的积水方格总数为 \(3\)。

---

试题中使用的生成数列 \(R\) 定义如下：整数 \(0\leq R_1\lt 201701\) 在输入中给出。

对于 \(i\gt 1,R_i=(R_{i−1}\times 6807+2831)\mod 201701\)。

输入格式

两个整数 \(n,R_1\)，表示屋顶的宽度和生成数列的首项。从左向右数第 \(i(1\leq i\leq n)\) 个瓦片的高度 \(a_i=R_i\mod 10\)。

输出格式

一个整数，表示暴雨后屋顶积水方格的总数。

输入输出样例 #1

输入 #1

10 1

输出 #1

23

说明/提示

\(1\leq n\leq100\)。

本题原始满分为 \(15\text{pts}\)。

gpt分析

这个问题是经典的接雨水（Trapping Rain Water）问题。我们可以使用双指针或者前后缀数组的方法高效计算积水量。

---

解题思路

1. 生成瓦片高度
   题目要求根据给定的递推公式生成瓦片高度：
   [
   a_i = R_i \mod 10
   ]
   [
   R_i = (R_{i-1} \times 6807 + 2831) \mod 201701
   ]
   我们可以直接按照这个公式依次计算 ( R_i ) 并存储其对应的 ( a_i )。

2. 计算每个位置的积水量
   关键点：对于第 ( i ) 个位置，它能存的水取决于它左侧的最高瓦片和右侧的最高瓦片中的较小者：
   [
   \text{water}[i] = \max(0, \min(\text{leftMax}[i], \text{rightMax}[i]) - a[i])
   ]

   • leftMax[i] 表示位置 ( i ) 左边（包括自己）的最大高度
   • rightMax[i] 表示位置 ( i ) 右边（包括自己）的最大高度
   • 取两者的较小值，减去当前位置的高度 ( a[i] )，得到积水量

3. 计算总积水量
   直接累加所有位置的积水。

---

代码实现

我们使用 O(n) 预处理 leftMax 和 rightMax，然后 O(n) 计算积水量，整体时间复杂度是 O(n)，完全适用于 n ≤ 100 的范围。

#include <iostream>
using namespace std;

const int MAX_N = 100; 
int a[MAX_N]; // 瓦片高度
int leftMax[MAX_N], rightMax[MAX_N];

int main() {
    int n, R;
    cin >> n >> R;

    // 生成瓦片高度
    for (int i = 0; i < n; ++i) {
        a[i] = R % 10;
        R = (R * 6807 + 2831) % 201701;
    }

    // 计算 leftMax 数组
    leftMax[0] = a[0];
    for (int i = 1; i < n; ++i) {
        leftMax[i] = max(leftMax[i - 1], a[i]);
    }

    // 计算 rightMax 数组
    rightMax[n - 1] = a[n - 1];
    for (int i = n - 2; i >= 0; --i) {
        rightMax[i] = max(rightMax[i + 1], a[i]);
    }

    // 计算总积水量
    int totalWater = 0;
    for (int i = 0; i < n; ++i) {
        totalWater += max(0, min(leftMax[i], rightMax[i]) - a[i]);
    }

    cout << totalWater << endl;
    return 0;
}

---

代码解析

1. 生成瓦片高度：

   • 通过给定递推公式计算 ( R_i )，并取 R_i % 10 得到瓦片高度 a[i]。

2. 预处理 leftMax 和 rightMax：

   • leftMax[i] 存储从 左到右扫描 时的最高高度。
   • rightMax[i] 存储从 右到左扫描 时的最高高度。

3. 计算积水量：

   • 对于每个位置，积水量是 min(leftMax[i], rightMax[i]) - a[i]，若为负则取 0。

4. 输出最终结果。

---

复杂度分析

• 生成瓦片高度：O(n)
• 计算 leftMax 和 rightMax：O(n)
• 计算积水量：O(n)
• 总时间复杂度：O(n)，适用于 n ≤ 100。

---

示例运行

输入

10 1

计算过程

生成的瓦片高度：

1 5 7 2 3 1 4 8 9 6

计算 leftMax：

1 5 7 7 7 7 7 8 9 9

计算 rightMax：

9 9 9 9 9 9 9 9 9 6

计算积水：

8 0 0 5 4 6 3 0 0 0

积水总量 = 23

输出

23

---

总结

这个方法利用前缀和后缀最大值预处理，时间复杂度 O(n)，非常高效，适用于这道题的限制条件。