数据结构与算法之美-5 排序算法2

本文地址

12 | 排序（下）：如何用快排思想在O(n)内查找第K大元素？

归并排序和快速排序比较

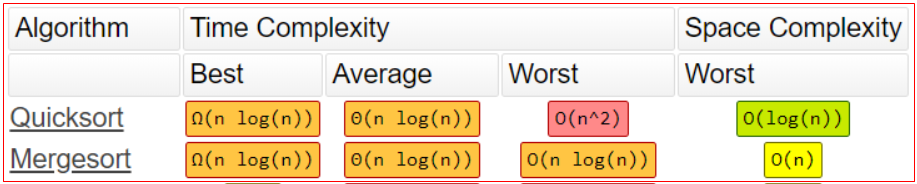
归并排序和快速排序的平均时间复杂度都是 O(nlogn)，但是归并排序的时间复杂度比较稳定
归并排序是稳定的排序算法，快速排序不是稳定的排序算法
归并排序空间复杂度是 O(n)(因为合并函数无法在原地执行)，快速排序空间复杂度是 O(logn)(主要是递归造成的栈空间的使用)

归并排序和快速排序用的都是分治的思想，代码都通过递归来实现，过程非常相似。
- 归并排序的处理过程是由下到上的，先处理子问题，然后再合并；而快排正好相反，它的处理过程是由上到下的，先分区，然后再处理子问题
- 理解归并排序的重点是理解递推公式和 merge() 合并函数，理解快排的重点也是理解递推公式和 partition() 分区函数
归并排序算法是一种在任何情况下时间复杂度都比较稳定的排序算法，但是它存在致命的缺点，即归并排序不是原地排序算法，空间复杂度是 O(n)。正因为此，归并排序没有快速排序应用广泛。
快速排序算法平均情况下时间复杂度是 O(nlogn)。虽然最坏情况下的时间复杂度是 O(n^2)，但是时间复杂度退化到 O(n^2) 的概率非常小，我们可以通过合理地选择 pivot 来避免这种情况。

归并排序 Merge Sort

如果要排序一个数组，我们先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。

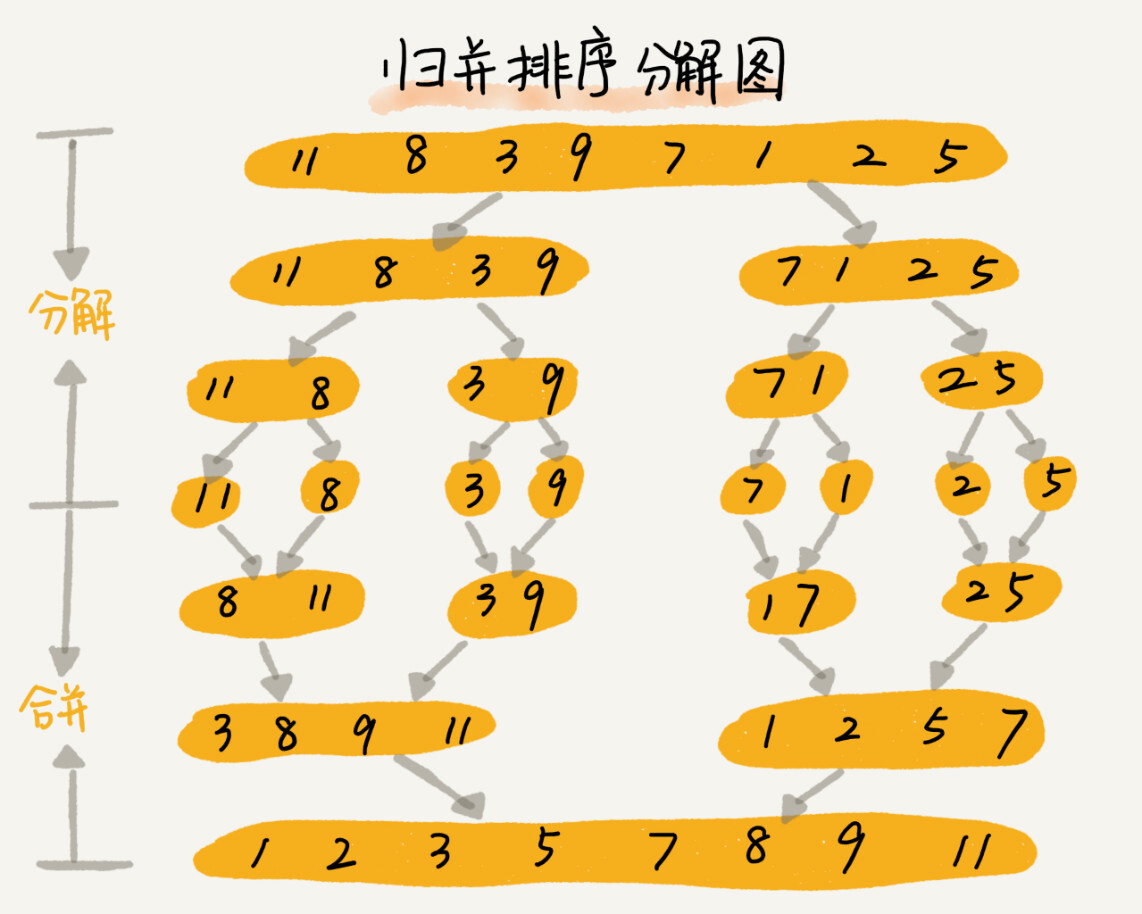
归并排序使用的就是分治思想，将一个大问题分解成小的子问题来解决，小的子问题解决了，大问题也就解决了。

分治算法一般都是用递归来实现的，分治是一种解决问题的处理思想，递归是一种编程技巧。

代码实现

要想写出归并排序的代码，我们先写出归并排序的递推公式。

递推公式：merge_sort(p,r) = merge(merge_sort(p,q), merge_sort(q+1,r))
终止条件：p >= r 不用再继续分解

其中 merge_sort(p,r) 表示：给下标从 p 到 r 之间的数组排序
我们将这个排序问题转化为了两个子问题：merge_sort(p,q) 和 merge_sort(q+1,r)，其中下标 q 等于 p 和 r 的中间位置，也就是 (p+r)/2
当下标从 p 到 q 和从 q+1 到 r 这两个子数组都排好序之后，我们再将两个有序的子数组合并在一起，这样下标从 p 到 r 之间的数据就也排好序了

// 归并排序算法，A是数组，n表示数组大小
merge_sort(A) {
  merge_sort_c(A, 0, n-1)
}

// 递归调用函数
merge_sort_c(A, p, r) {
  // 递归终止条件
  if p >= r  then return

  // 取 p 到 r 之间的中间位置 q
  q = (p+r) / 2
  // 分治递归
  merge_sort_c(A, p, q)
  merge_sort_c(A, q+1, r)
  // 将已经有序的两个子数组 A[p,q] 和 A[q+1,r] 合并为一个有序的数组 A[p,r]
  merge(A[p,r], A[p,q], A[q+1,r])
}

合并函数分析

上述合并函数 merge(A[p,r], A[p,q], A[q+1,r]) 的作用是：将已经有序的两个子数组 A[p,q] 和 A[q+1,r] 合并为一个有序的数组 A[p,r]，那这个过程具体该如何做呢？

我们申请一个临时数组 tmp，大小与 A[p,r] 相同。我们用两个游标 i 和 j，分别指向 A[p,q] 和 A[q+1,r] 的第一个元素。比较这两个元素 A[i] 和 A[j]，如果 A[i]<=A[j]，我们就把 A[i] 放入到临时数组 tmp，并且 i 后移一位，否则将 A[j] 放入到数组 tmp，j 后移一位。

继续上述比较过程，直到其中一个子数组中的所有数据都放入临时数组中，再把另一个数组中的数据依次加入到临时数组的末尾，这个时候，临时数组中存储的就是两个子数组合并之后的结果了。最后再把临时数组 tmp 中的数据拷贝到原数组 A[p,r]中。

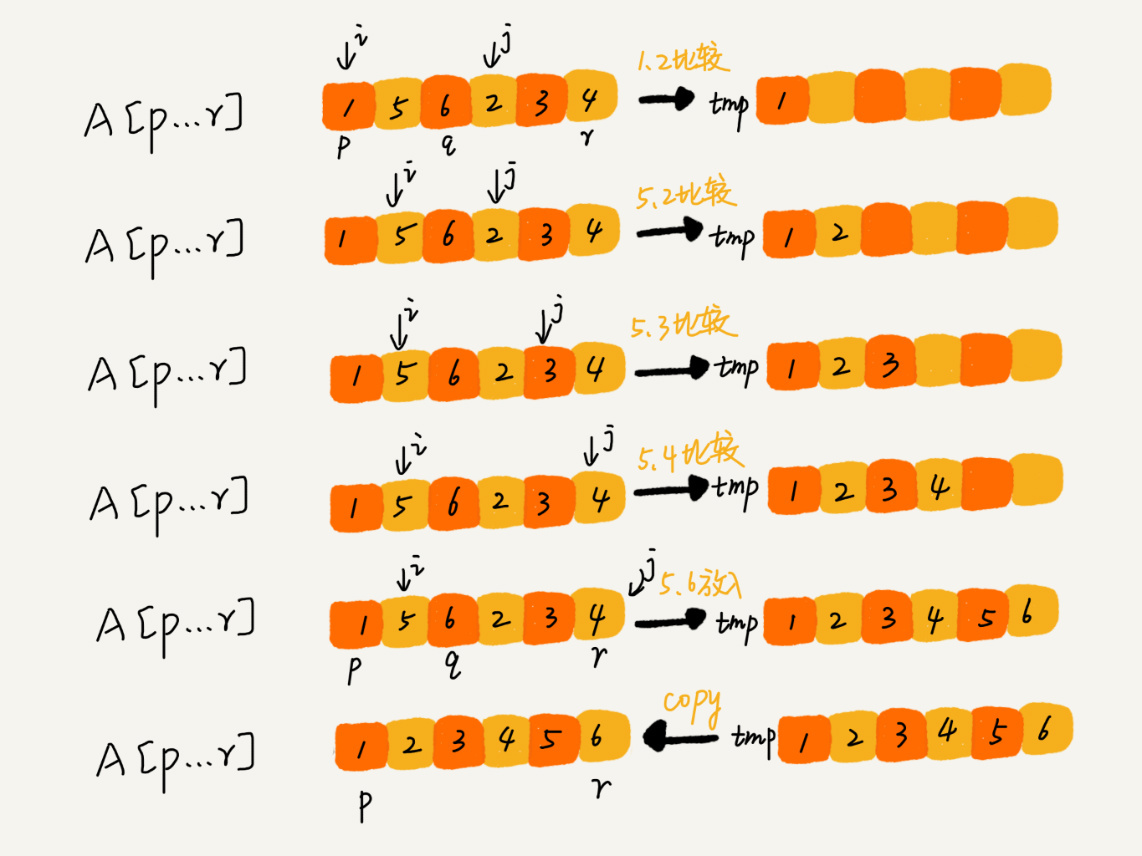
稳定性分析

归并排序稳不稳定关键要看 merge() 函数，也就是两个有序子数组合并成一个有序数组的那部分代码。

在合并的过程中，如果两个有序子数组之间有值相同的元素，那我们可以先把第一个有序子数组中的元素放入 tmp 数组。这样就保证了值相同的元素，在合并前后的先后顺序不变。所以，归并排序是一个稳定的排序算法。

时间复杂度

不仅递归求解的问题可以写成递推公式，递归代码的时间复杂度也可以写成递推公式。

如果我们定义求解问题 a 的时间是 T(a)，求解问题 b、c 的时间分别是 T(b) 和 T(c)，那我们就可以得到这样的递推关系式：

T(a) = T(b) + T(c) + K       // 其中 K 等于将两个子问题 b、c 的结果合并成问题 a 的结果所消耗的时间

我们假设对 n 个元素进行归并排序需要的时间是 T(n)，那分解成两个子数组排序的时间都是 T(n/2)。所以，套用前面的公式，归并排序的时间复杂度的计算公式就是：

T(1) = C；              n = 1   // n = 1 时，只需要常量级的执行时间，所以表示为 C
T(n) = 2 * T(n/2) + n； n > 1   // 合并两个有序子数组的时间复杂度是 O(n)

我们再进一步分解一下计算过程

T(n) = 2*T(n/2) + n
     = 2*(2*T(n/4) + n/2) + n     = 4*T(n/4) + 2*n
     = 4*(2*T(n/8) + n/4) + 2*n   = 8*T(n/8) + 3*n
     = 8*(2*T(n/16) + n/8) + 3*n  = 16*T(n/16) + 4*n
     ......
     = 2^k * T(n/2^k) + k * n

通过这样一步一步分解推导，我们可以得到 T(n) = 2^k * T(n/2^k) + kn。当 T(n/2^k)=T(1) 时，也就是 n/2^k = 1，我们得到 k=logn 。我们将 k 值代入上面的公式，得到 T(n) = Cn + nlogn。用大 O 标记法来表示的话，T(n) 就等于 O(nlogn)。所以归并排序的时间复杂度是 O(nlogn)。

可以看出，归并排序的执行效率与要排序的原始数组的有序程度无关，所以其时间复杂度是非常稳定的，不管是最好情况、最坏情况，还是平均情况，时间复杂度都是 O(nlogn)。

空间复杂度

归并排序的时间复杂度任何情况下都是 O(nlogn)，看起来非常优秀，但是，归并排序并没有像快排那样应用广泛，这是为什么呢？因为它有一个致命的弱点，那就是归并排序不是原地排序算法。

这是因为归并排序的合并函数，在合并两个有序数组为一个有序数组时，需要借助额外的存储空间。但是，归并排序的空间复杂度到底是多少呢？

递归代码的空间复杂度并不能像时间复杂度那样累加，因为，尽管每次合并操作都需要申请额外的内存空间，但在合并完成之后，临时开辟的内存空间就被释放掉了。在任意时刻，CPU 只会有一个函数在执行，也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小，所以空间复杂度是 O(n)。

快速排序 Quick Sort

快排的原理

快排利用的也是分治思想，它有点像归并排序，但是思路其实完全不一样：

如果要排序数组中下标从 p 到 r 之间的一组数据，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点）
我们遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间
经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot 的
根据分治、递归的处理思想，我们可以用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据，直到区间缩小为 1，就说明所有的数据都有序了

快排的伪代码实现

递推公式：quick_sort(p,r) = quick_sort(p,q-1) + quick_sort(q+1,r)
终止条件：p >= r

// 快速排序，A是数组，n表示数组的大小
quick_sort(A) {
  quick_sort_c(A, 0, n-1)
}
// 快速排序递归函数，p,r为下标
quick_sort_c(A, p, r) {
  if p >= r then return

  q = partition(A, p, r) // 获取分区点，这是快排的核心
  quick_sort_c(A, p, q-1)
  quick_sort_c(A, q+1, r)
}

//原地分区函数
partition(A, p, r) {
  pivot = A[r]
  i = p
  for j = p to r-1 do {
    if A[j] < pivot {
      swap A[i] with A[j]
      i = i+1
    }
  }
  swap A[i] with A[r]
  return i

快排的性能分析

快排是一种原地、不稳定的排序算法。

因为分区的过程涉及交换操作，如果数组中有两个相同的元素，在分区操作之后，相同元素的相对先后顺序就可能会改变。所以，快速排序并不是一个稳定的排序算法。

快排也是用递归来实现的。对于递归代码的时间复杂度，我前面总结的公式，这里也还是适用的。如果每次分区操作，都能正好把数组分成大小接近相等的两个小区间，那快排的时间复杂度递推求解公式跟归并是相同的，此时，快排的时间复杂度也是 O(nlogn)。

但是，公式成立的前提是每次分区操作，我们选择的 pivot 都很合适，正好能将大区间对等地一分为二。但实际上这种情况是很难实现的。此时使用递推求解的话过程非常复杂。实际上，递归的时间复杂度的求解方法除了递推公式之外，还有递归树，这里暂时不说。

这里直接给出结论：快排在大部分情况下的时间复杂度都可以做到 O(nlogn)，只有在极端情况下，才会退化到 O(n^2)。而且，我们也有很多方法将这个概率降到很低。

比如：找三个数，分别是两个端点以及中数，找这三个数的中间数作为 pivot 来尽量将数组能够划开一些，这样出现一头大一头小的概率会比较小。

快排过程讲解-1

参考文章

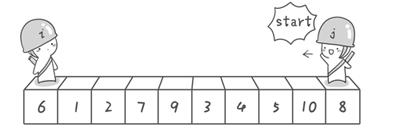
假设我们现在对6 1 2 7 9 3 4 5 10 8这个序列进行排序。首先在这个序列中随便找一个数作为基准数。为了方便，就让第一个数 6 作为基准数吧。接下来，需要将这个序列中所有比基准数大的数放在 6 的右边，比基准数小的数放在 6 的左边。

在初始状态下，数字 6 在序列的第 1 位。我们的目标是将 6 挪到序列中间的某个位置，假设这个位置是 k。现在就需要寻找这个 k，并且以第 k 位为分界点，左边的数都小于等于 6，右边的数都大于等于 6。

方法其实很简单：分别从初始序列的两端开始探测，先 从右往左 找一个小于 6 的数，再 从左往右 找一个大于 6 的数，然后交换他们。这里可以用两个变量(哨兵) i 和 j，分别指向序列最左边和最右边。

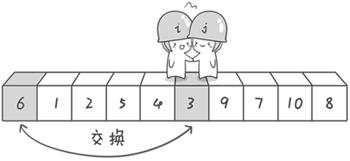
刚开始的时候让哨兵 i 指向序列的最左边(即 i = 1，i 指向数字 6)，让哨兵 j 指向序列的最右边(即 j = 10，指向数字 8)。

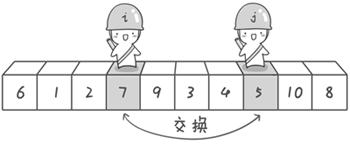
首先哨兵 j 开始出动，哨兵 j 一步一步地向左挪动（即 j-–），直到找到一个小于 6 的数（即数字 5）停下来。然后哨兵 i 再一步一步向右挪动（即 i++），直到找到一个数大于 6 的数（即数字 7）停下来。

原文说：因为此处设置的基准数是最左边的数，所以需要让哨兵 j 先出动，这一点非常重要。
实际上：实现方案不止这一种，并非一定要按照作者的思路来实现。

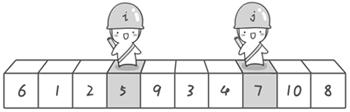
现在交换哨兵 i 和哨兵 j 所指向的元素的值，交换之后的序列如下：

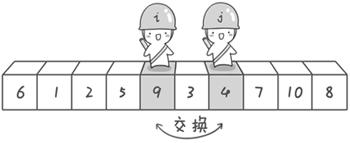
接下来开始哨兵 j 继续向左挪动，直到找到 4 后停了下来；哨兵 i 也继续向右挪动的，直到找到 9 之后停了下来。

此时再次进行交换，交换之后的序列如下：

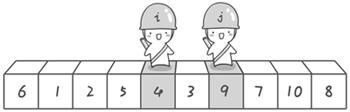
接下来开始哨兵 j 继续向左挪动，直到找到 3 后又停了下来；哨兵 i 继续向右移动，糟啦，此时哨兵 i 和哨兵 j 相遇了，说明此时探测结束。

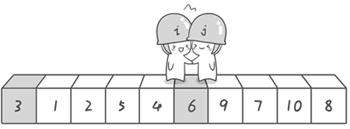
我们将基准数 6 和 3 进行交换，交换之后的序列如下：

到此第一轮探测结束。此时以基准数 6 为分界点，6 左边的数都小于等于 6，6 右边的数都大于等于 6。

回顾一下刚才的过程，其实哨兵 j 的使命就是要找小于基准数的数，而哨兵 i 的使命就是要找大于基准数的数，直到 i 和 j 碰头为止。

现在基准数 6 已经归位，它已经处在最终排序序列的正确的位置。此时我们已经将原来的序列以 6 为分界点拆分成了两个子序列，接下来分别处理这两个子序列即可。

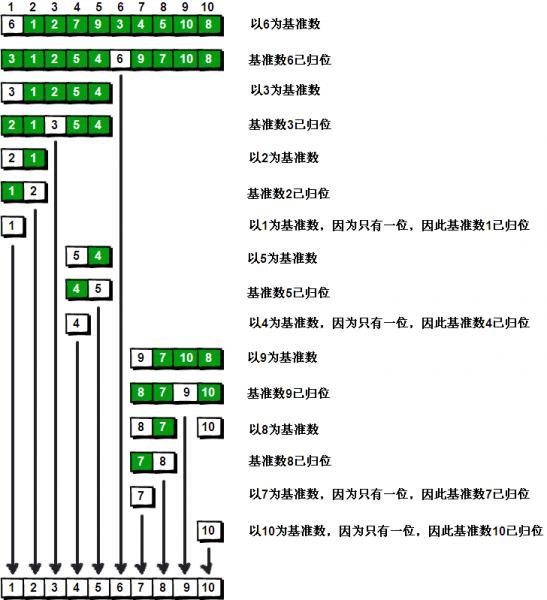
快速排序的每一轮处理其实就是将这一轮的基准数归位，直到所有的数都归位为止，排序就结束了。

快速排序之所比较快，因为相比冒泡排序，每次交换是跳跃式的。每次排序的时候设置一个基准点，将小于等于基准点的数全部放到基准点的左边，将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样每次只能在相邻的数之间进行交换，交换的距离就大的多了。因此总的比较和交换次数就少了，速度自然就提高了。当然在最坏的情况下，仍可能是相邻的两个数进行了交换。

快排的过程讲解-2

for each (unsorted) partition
set first element as pivot
  storeIndex = pivotIndex + 1
  for i = pivotIndex + 1 to rightmostIndex
    if element[i] < element[pivot]
      swap(i, storeIndex); storeIndex++
  swap(pivot, storeIndex - 1)

Working on partition [3,44,38,5,47,15,36,26,27,2,46,4,19,50,48] (index 0 to 14). Selecting 3 as pivot (pivotIndex = 0, storeIndex = pivotIndex + 1 = 0 + 1 = 1)
- Checking if 44 < 3 (pivot), Checking if 38 < 3 (pivot)......Checking if 2 < 3 (pivot). 2 < 3 (pivot) is true.
  - Swapping 2 (index = 9) with element 44 (storeIndex = 1). set storeIndex = storeIndex + 1 = 1 + 1 = 2.
  - current partition is [3,2,38,5,47,15,36,26,27,44,46,4,19,50,48]
- Checking if 46 < 3 (pivot), Checking if 4 < 3 (pivot)......
- Iteration complete.
  - Swapping pivot (index = 0, value = 3) with element at storeIndex - 1 (index = 2 - 1 = 1, value = 2).
  - current partition is [2,3,38,5,47,15,36,26,27,44,46,4,19,50,48]
  - Pivot 3 is now at its sorted position.
Working on partition [2] (index 0 to 0). Since partition size == 1, element inside partition is necessarily at sorted position.
Working on partition [38,5,47,15,36,26,27,44,46,4,19,50,48] (index 2 to 14). Selecting 38 as pivot. (pivotIndex = 2, storeIndex = pivotIndex + 1 = 2 + 1 = 3)
- Checking if 5 < 38 (pivot). 5 < 38 (pivot) is true.
  - Swapping 5 (index = 3) with element 5 (storeIndex = 3). (实际上不需要交换)
  - set storeIndex = storeIndex + 1 = 3 + 1 = 4. (但是保存的索引需要 + 1)
- Checking if 15 < 38 (pivot). 15 < 38 (pivot) is true.
  - Swapping 15 (index = 5) with element 47 (storeIndex = 4). set storeIndex = storeIndex + 1 = 4 + 1 = 5.
  - current partition is [38,5,15,47,36,26,27,44,46,4,19,50,48]
- Checking if 36 < 38 (pivot). 36 < 38 (pivot) is true.
  - Swapping 36 (index = 6) with element 47 (storeIndex = 5). set storeIndex = storeIndex + 1 = 5 + 1 = 6.
  - current partition is [38,5,15,36,47,26,27,44,46,4,19,50,48]
- Checking if 26 < 38 (pivot). 26 < 38 (pivot) is true.
  - Swapping 26 (index = 7) with element 47 (storeIndex = 6). set storeIndex = storeIndex + 1 = 6 + 1 = 7.
  - current partition is [38,5,15,36,26,47,27,44,46,4,19,50,48]
- Checking if 27 < 38 (pivot). 27 < 38 (pivot) is true.
  - Swapping 27 (index = 8) with element 47 (storeIndex = 7). set storeIndex = storeIndex + 1 = 7 + 1 = 8.
  - current partition is [38,5,15,36,26,27,47,44,46,4,19,50,48]
- Checking if 44 < 38 (pivot). Checking if 46 < 38 (pivot). Checking if 4 < 38 (pivot). 4 < 38 (pivot) is true.
  - Swapping 4 (index = 11) with element 47 (storeIndex = 8). set storeIndex = storeIndex + 1 = 8 + 1 = 9.
  - current partition is [38,5,15,36,26,27,4,44,46,47,19,50,48]
- Checking if 19 < 38 (pivot). 19 < 38 (pivot) is true.
  - Swapping 19 (index = 12) with element 44 (storeIndex = 9). set storeIndex = storeIndex + 1 = 9 + 1 = 10.
  - current partition is [38,5,15,36,26,27,4,19,46,47,44,50,48]
- Checking if 50 < 38 (pivot). Checking if 48 < 38 (pivot).
- Iteration complete.
  - Swapping pivot (index = 2, value = 38) with element at storeIndex - 1 (index = 10 - 1 = 9, value = 19).
  - current partition is [19,5,15,36,26,27,4,38,46,47,44,50,48]
  - Pivot 38 is now at its sorted position.

current partition is [19,5,15,36,26,27,4,(38),46,47,44,50,48]

Working on partition [19,5,15,36,26,27,4] (index 2 to 8)...
- Working on partition [4,5,15] (index 2 to 4)...
  - Working on partition [5,15] (index 3 to 4)...
    - Working on partition [15] (index 4 to 4)...
- Working on partition [26,27,36] (index 6 to 8)...
  - Working on partition [27,36] (index 7 to 8)...
    - Working on partition [36] (index 8 to 8)...
Working on partition [46,47,44,50,48] (index 10 to 14)...
- Working on partition [44] (index 10 to 10)...
- Working on partition [47,50,48] (index 12 to 14)...
  - Working on partition [50,48] (index 13 to 14)...
    - Working on partition [48] (index 13 to 13)...

解答开篇

快排核心思想就是分治和分区，我们可以利用分区的思想，来解答开篇的问题：O(n) 时间复杂度内求无序数组中的第 K 大元素。

我们选择数组区间 A[0,n-1] 的最后一个元素 A[n-1] 作为 pivot，对数组 A[0,n-1] 原地分区，这样数组就分成了三部分，A[0,p-1]、A[p]、A[p+1,n-1]。

如果 p+1=K，那 A[p] 就是要求解的元素
如果 K>p+1, 说明第 K 大元素出现在 A[p+1,n-1] 区间，我们再按照上面的思路递归地在 A[p+1,n-1] 这个区间内查找
如果 K<p+1，那我们就在 A[0...p-1] 区间查找

为什么上述解决思路的时间复杂度是 O(n)？

第一次分区查找，我们需要对大小为 n 的数组执行分区操作，需要遍历 n 个元素。
第二次分区查找，我们只需要对大小为 n/2 的数组执行分区操作，需要遍历 n/2 个元素。
依次类推，分区遍历元素的个数分别为 n/2、n/4、n/8、n/16……直到区间缩小为 1。
如果我们把每次分区遍历的元素个数加起来，就是：n + n/2 + n/4 + n/8 + ... + 1。这是一个等比数列求和，最后的和等于 2n-1。
所以，上述解决思路的时间复杂度就为 O(n)。

2021-8-7

posted @ 2021-08-07 23:24 白乾涛阅读(106) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

白乾涛

个人站点(baiqiantao.github.io) 我的GitHub(github.com/baiqiantao)