Leetcode_动态规划_爬楼梯

70. 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

 

class Solution {
public:
    int climbStairs(int n) {
        if(n <= 1)
            return n;
        int* dp = new int[n+1];       //注意这里new分配空间
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 2;
        for(int i=3;i<=n; i++){
            dp[i] = dp[i-1]+dp[i-2];
        }
        return dp[n];
    }
};

优化版本：

class Solution {
public:
    int climbStairs(int n) {
        int p = 0, q = 0, r = 1;
        for (int i = 1; i <= n; ++i) {
            p = q; 
            q = r; 
            r = p + q;
        }
        return r;
    }
};

　　

62. 不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？ 

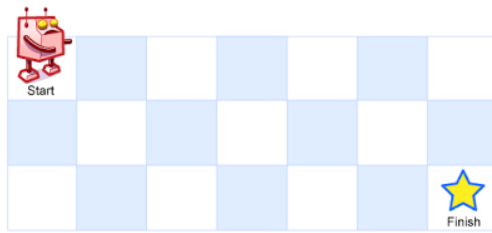
例如，上图是一个7 x 3 的网格。有多少可能的路径？

class Solution {
public:
    int uniquePaths(int m, int n) {
        if(m<=0 || n<=0){
            return 0;
        }
        vector<vector<int>> dp(m,vector<int>(n, 0));
        for(int i=0; i<m;i++){
            dp[i][0] = 1;
        }
        for(int j=0;j<n;j++){
            dp[0][j] = 1;
        }
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                dp[i][j] = dp[i-1][j]+dp[i][j-1];
                cout<<dp[i][j]<<" ";
            }
            cout<<endl;
        }
        return dp[m-1][n-1];
    }
};

优化-复用：

 

#include <iostream>
#include <vector>
using namespace std;

class Solution{
public:
    int uniquePaths(int m, int n){
        if(m<=0 || n<=0){
            return 0;
        }
        vector<int> dp(n, 1);
        for(int i=1; i<m; i++){
            for(int j=1; j<n; j++){
                dp[j] = dp[j] + dp[j-1];
                cout<<dp[j]<<" ";
            }
            cout<<endl;
        }
        return dp[n-1];
    }
};

int main(){
    Solution s;
    s.uniquePaths(3, 4);
    return 0;
}

303. 区域和检索 - 数组不可变

给定一个整数数组  nums，求出数组从索引 i 到 j  (i ≤ j) 范围内元素的总和，包含 i,  j 两点。

示例：

给定 nums = [-2, 0, 3, -5, 2, -1]，求和函数为 sumRange()

sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3

#include <iostream>
#include <vector>
using namespace std;

class NumArray {
public:
    vector<int> dp;
    NumArray(vector<int>& nums) {
        dp.resize(nums.size()+1);
        dp[0] = nums[0];
        for(int i=1; i<nums.size();i++){
            dp[i] = dp[i-1] + nums[i];
        }
    }
    
    int sumRange(int i, int j) {
        return dp[j] - dp[i];   
    }
};


int main(){
    vector<int> num = {-2, 0, 3, -5, 2, -1};
    NumArray s(num);
    cout<<s.sumRange(0, 3)<<endl;
    return 0;
}

理解：依次求和，时间复杂度很高。这里使用了类似动态规划的方式。。。