白昊翔

导航

 
数据结构之重中之重-----二叉树基础

二叉树是数据结构中的非常重要的概念；对初学者来讲这是数据结构的承上启下部分。

看二叉树有一段时间了，这里做一个相应的总结。

需要掌握的术语：

度：1.结点的度：子树个数；

　　2.  树的度：结点度的最大值；

叶子 ：度==0的结点；（终端结点）

分支：度！=0的结点；（非终端结点）

孩子：某结点的子树的根节点；

双亲：与孩子对应；

兄弟：同样双亲；

路径长度：经过的边数；

祖先：直系关联的上层；

子孙：与祖先对应；

有序树：交换各结点位置树发生变化；

无序树：反之；

------------------------------------------------------

二叉树的递归建树过程：（前序建树）

Node *Bitree::Creat(Node *p)
{
    DataType ch;
    cin>>ch;
    if(ch!='#')
        p=NULL;
    else
    {
        p=new Node;
        p->A=ch;
        p->Left=Creat(p->Left);
        p->Right=Creat(p->Right);
    }
    Root=p;
    return p;
}
View Code

 

二叉树的递归遍历操作：（依旧用前序为例）

1 void *Bitree::Print(Node *p)
2 {
3     if(p==NULL)
4         return;
5     cout<<p->A<<' ';
6     Print(p->Left);
7     Print(p->Right);
8     return;
9 }
View Code

 

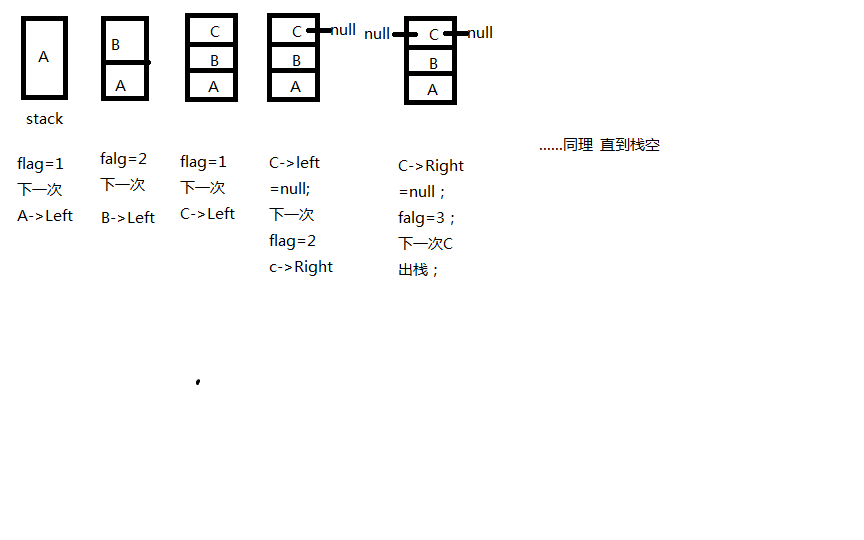
二叉树非递归建树过程：

方法：

用栈来控制进出；

然后当flag==1；表示需要建立栈顶元素的左孩子；

　　　flag==2；表示需要建立栈顶元素的右孩子；

　　　flag==3；表示右孩子建立完成需要出栈；

假设：ABC###D##

  1 #include<iostream>
  2 using namespace std;
  3 #ifndef BITREE
  4 #define BITREE
  5 typedef char DataType;
  6 struct Node 
  7 {
  8     DataType A;
  9     Node *Left,*Right;
 10 };
 11 class Bitree
 12 {
 13     Node *Root;
 14 public:
 15     Bitree(){Root=NULL;}
 16     void Creat();        
 17     void Remove();
 18     void Sort();
 19     void Print(Node *p)const;
 20     Node *GetRoot();
 21 };
 22 void Bitree::Creat()
 23 {
 24     Node *stack[100];int top=-1;
 25     char ch;
 26     cin>>ch;
 27     int flag=1;
 28     if(ch=='#')
 29         return;
 30     Root=new Node;
 31     Root->A=ch;
 32     Root->Left=NULL;
 33     Root->Right=NULL;
 34 
 35     stack[++top]=Root;
 36     while(top!=-1)
 37     {
 38         Node *p;
 39         
 40 
 41         if(flag==1)
 42         {
 43             cin>>ch;
 44             if(ch=='#')
 45             {
 46                 flag=2;
 47             }
 48             else
 49             {
 50                 p=new Node;
 51                 p->A=ch;
 52                 p->Left=NULL;
 53                 p->Right=NULL;
 54                 stack[top]->Left=p;
 55                 stack[++top]=p;
 56                 flag=1;
 57             }
 58         }
 59         else if(flag==2)
 60         {
 61             cin>>ch;
 62             if(ch=='#')
 63             {
 64                 flag=3;
 65             }
 66             else
 67             {
 68                 p=new Node;
 69                 p->A=ch;
 70                 p->Left=NULL;
 71                 p->Right=NULL;
 72                 stack[top]->Right=p;
 73                 stack[++top]=p;
 74                 flag=1;
 75             }
 76         }
 77         else if(flag==3)
 78         {
 79             Node *temp;
 80             temp = stack[top--];            
 81             while (top >= 0 && stack[top]->Right == temp)   
 82                 --top;
 83             flag=2;
 84         }
 85     }
 86 }
 87 void Bitree::Print(Node *p)const
 88 {
 89     if(p==NULL)
 90         return;
 91     cout<<p->A<<' ';
 92     Print(p->Left);
 93     Print(p->Right);
 94     return;
 95 }    
 96 Node *Bitree::GetRoot()
 97 {
 98     return Root;
 99 }
100 #endif
101 int main()
102 {
103     Bitree B;
104     B.Creat();
105     B.Print(B.GetRoot());
106 }
View Code

二叉树的递归求深度

 

int Bitree::Depth(Node *p)
{
    if(p==NULL)
    {
        return 0;
    }    
    int left=1;
    int right=1;
    left+=Depth(p->Left);
    right+=Depth(p->Right);
    return left>right?left:right;

}

 

 

二叉树的非递归求深度

方法：层序遍历每一层Depth++即可；

 

int TreeDepth(TreeNode* pRoot)
    {
     queue<TreeNode*> q;
        if(!pRoot) return 0;
        q.push(pRoot);
        int level=0;
        while(!q.empty()){
            int len=q.size();
            level++;
            while(len--){
                TreeNode* tem=q.front();
                q.pop();
                if(tem->left) q.push(tem->left);
                if(tem->right) q.push(tem->right);
            }
        }
        return level;
    }

 

二叉树前序遍历非递归写法；

 

void Bitree::PreOrder(Node *p)
{
    Node *stack[100];
    int top=-1;
    while(p!=NULL&&top!=-1)
    {
        while(p!=NULL)
        {
            cout<<p->A;
            stack[++top]=p;
            p=p->Left;
        }
        if(top!=-1)
        {
            p=stack[top--];
            p=p->Right;
        }

    }

}

 

 

 

二叉树删除子树；

方法：

先找到删除子树的双亲，然后双亲结点赋空；把子树的每一个地址前序遍历入栈；

对每一个地址进行delete；

 

 

二叉树层序遍历递归队列写法：

 

 1 //递归写法
 2 #include<iostream>
 3 using namespace std;
 4 #include<queue>
 5 struct Node 
 6 {
 7     struct Node *Left,*Right;
 8     char data;
 9 };
10 class Bitree
11 {
12     queue<Node *> s;
13     Node *root;
14 public:
15     Bitree(){root=NULL;}
16     Node *Create(Node *);
17     void Print(Node *);
18     Node *Getroot();
19     void CCC();
20 };
21 Node *Bitree::Create(Node *p)
22 {
23     char ch;
24     cin>>ch;
25     if(ch=='#')
26         p=NULL;
27     else
28     {
29         p=new Node;
30         p->data=ch;
31         p->Left=Create(p->Left);
32         p->Right=Create(p->Right);
33  
34     }
35     root=p;
36     return p;
37 }
38 void Bitree::Print(Node *p)
39 {
40     cout<<p->data<<' ';
41     if(p->Left!=NULL)
42         s.push(p->Left);
43     if(p->Right!=NULL)
44         s.push(p->Right);
45     s.pop();
46     if(!s.empty())
47         Print(s.front());
48 }
49 void Bitree::CCC()
50 {
51     s.push(root);
52     Print(s.front());
53 }
54 Node * Bitree::Getroot()
55 {
56     return root;
57 }
58 int main()
59 {
60     Bitree l;
61     l.Create(l.Getroot());
62     l.CCC();
63 }
View Code

 

 

 

二叉树层序遍历递归用深度求：

 1 //递归写法
 2 #include<iostream>
 3 #include<queue>
 4 using namespace std;
 5  
 6 struct Node 
 7 {
 8     char A;
 9     Node *Left,*Right;
10 };
11 class Bitree
12 {
13     Node *Root;
14     queue<Node *> Dui;
15 public:
16     Bitree(){Root=NULL;};
17     Node *Create(Node *);
18     int Depth(Node* pRoot);//计算二叉树深度;
19     void Print(Node *p,int level);
20     void ARR(Node *p);
21     Node * Back();
22 };
23 Node *Bitree::Create(Node *p)
24 {
25     char ch;
26     cin>>ch;
27     if(ch=='#')
28         p=NULL;
29     else
30     {
31         p=new Node ;
32         p->A=ch;
33         p->Left=Create(p->Left);
34         p->Right=Create(p->Right);
35     }
36     Root=p;
37     return p;
38 }
39 Node * Bitree::Back()
40 {
41     return Root;
42 }
43 void Bitree::Print(Node *p,int level)
44 {
45     if(p==NULL||level<1)
46         return;
47     else if(level==1)
48     {
49         cout<<p->A<<' ';
50         return;
51     }
52     Print(p->Left,level-1);
53     Print(p->Right,level-1);
54      
55 }
56 void Bitree::ARR(Node *p)
57 {
58     if(p==NULL)
59         return;
60     int depth=Depth(p);
61  
62     int i;
63     for(i=1;i<=depth;i++)
64     {
65         Print(p,i);
66  
67     }
68  
69 }
70 int Bitree::Depth(Node* pRoot)//计算二叉树深度
71 {
72     if(pRoot==NULL)//如果pRoot为NULL，则深度为0，这也是递归的返回条件
73         return 0;
74     //如果pRoot不为NULL，那么深度至少为1，所以left和right=1
75     int left=1;
76     int right=1;
77     left+=Depth(pRoot->Left);//求出左子树的深度
78     right+=Depth(pRoot->Right);//求出右子树深度
79   
80     return left>right?left:right;//返回深度较大的那一个
81 }
82 int main()
83 {
84     Bitree T;
85     T.Create(T.Back());
86     T.ARR(T.Back());
87     return 0;
88 }
View Code

 

判断完全二叉树的方法：

在队列里遍历，空树也存；

然后判断队列书否为空；

 

bool Bitree::Complete(Node *p)
{
    s.push(p);
    while((p=s.front())!=NULL)
    {
        s.pop();
        s.push(p->left);
        s.push(p->right);
    }
    while(!s.empty())
    {
        p=s.front();
        s.pop();
        if(p!=NULL)
        {
            return false;
        }
    }
    return true;
}

 

 

求二叉树宽度；

 

 1 void Bitree::Print(Node *p)
 2 {
 3     if(p==NULL)
 4     {
 5         cout<<0;
 6         return;
 7     }
 8     int Lastwidth=0;
 9     int MaxWidth=0;
10     s.push(Root);
11     p=Root;
12     MaxWidth=s.size();
13     while(!s.empty())
14     {
15         Lastwidth=s.size();
16         while(Lastwidth!=0)
17         {
18             p=s.front();
19             s.pop();
20             if(p->Left!=NULL)
21                 s.push(p->Left);
22             if(p->Right!=NULL)
23                 s.push(p->Right);
24             Lastwidth--;
25         }
26         MaxWidth=MaxWidth>s.size()?MaxWidth:s.size();
27     }
28     cout<<MaxWidth;
29     return;
30 }
View Code

 

 

 

----------- 一剑天涯-------------

posted on 2017-11-25 03:16  白昊翔  阅读(182)  评论(0)    收藏  举报
 
博客园  ©  2004-2026
浙公网安备 33010602011771号 浙ICP备2021040463号-3