250428 近期比赛总结
0423
ARC131 vp.
火速过了 AB 然后开始呆,C 发现不会博弈论,回去学了一点,D 发现只会写平方做法,E 看了一眼感觉比较困难,F 还没开始想。然后因为是本地数据好像还没有 sub 其实是可以骗分的但是我忘了。然后刚刚发现还忘了订题。
0424
qls 找了一套题.
三道感觉很数学的题。t1 最小的暴力都没跑过,然后场上没想到打表。t2 为什么没写??在写 t3,然后发现之前写的某道蓝书上的题可以搬一下(那天我还不知道这是莫反)。
下来看题解发现确实是神秘数学,发现不会神秘插值,不会莫反,不会杜教筛。
t2
是奇怪预处理 + 矩阵加速图上问题。
给一个单调不降序列的异或和,求原来可能的序列可能有多少。位数规模是 \(10^{18}\),\(n\le 16\)。
从高到低按位处理,因为序列是单调不降所以先处理出来所有的再除以阶乘是不太可做的,,所以把填到当前位的时候,\(a_{i}<a_{i+1}\) 用 \(1\) 表示,\(a_{i}=a{i+1}\) 用 \(0\) 表示,获得一个 \(01\) 序列,然后发现从上一位向下一位转移很有向图上问题,然后dfs 跑一跑发现状态数量其实非常的少,直接建图分段矩阵快速幂就好了。非常神奇的一题。
0425
好像没打比赛。
晚上打杭电春联,写了 3 题,开第 4 题时拼尽全力无法战胜,于是放弃。3 题分别是多测没清空/好像不开 longlong 见祖宗题,不知道建超级源点于是跑了 \(n\) 遍 dij 还以为是常数太大题,bitset 大法好题。
字符串哈希
两个字符串哈希函数,分别是
问有多少个长度不大于 \(k\) 的字符串可以有 \(B(s)^3\times c+B(s)^2\times d+B(s)\times e+f=A(s)\)。\(k\le 10\)
感觉当时又往容斥上跑了,然后还觉得这题需要推柿子。还想到跟 \(10007\) 有关,但是还是没想出来。这都没想出来??看看题解,因为 \(A(s)\) 没有哈希冲突,所以我们可以枚举最多有 \(10007\) 个不同的 \(B(s)\) 的值,按照给出的数求 \(A(s)\) 再反推 \(s\),然后计算一下 \(B(s)\) 看是不是相等。
0426
上午 jsyoi.
打这场的时候没困。但是还是因为太菜没有发挥出来什么。T1 是去年 SNOI 的原,太难了有点,然后也不会点减边,T2 刚好就是只想到了 \(O(n^3)\),然后写了性质,然后 T3 就是场上想起来一个曾经写过的题相关的结论很开心以为可以用然后发现用不了,然后推了一下性质写了交发现得到了 \(0\) 分的好成绩到底是为什么呢为什么呢为什么呢??想了半天也想不出来是为什么。个人感觉后两题的难度是小于 T1 的。
下午 cf div2.
感觉还是跟 cf 的题比较有缘分。A 喵了,B 很像省选 d1t1,更有缘分了,但是 wa 若干次,发现很多酒吧在同一个点上的情况还是考虑少了。C 是样例看不懂题,想了半天发现怎么这么牛啊!然后推推结论过了。发现是如果有同一天人数 \(\ge 4\) 是 \(Yes\),有形如 \(211112\)(中间是任意多个 \(1\),两边是 \(\ge 2\))的也可以。再推一推感觉没有什么别的东西了,然后急急急交了,过了。这场非常厉害的是前 \(3\) 题都有一车人过了,但是后三题都是个位数。后边想了想,但是没写出来,D 太困难放弃了。
0427
上午核桃周赛.
最近不是在学积性函数吗,然后很巧 T1 就带欧拉函数,但是其实我只知道欧拉函数是积性函数,然后我就不会了。写了 \(30pts\) 暴力。T2 是一个奇妙的博弈论题。T3 是一个比较麻烦但是因为我刚开始困了一会导致没写 \(O(nm)\) 暴力的题。
T2
给你一条序列,你和小 B 玩游戏,把一个棋子放到格子 \(s\) 上,每次可以选择把当前格子上的数字减 \(1\)(不为 \(0\) 的情况下),或者跳到 \([now+1,min(now+k,t)]\) 中的一个格子上。每次询问给一段区间的值加上 \(d\),或者对于给出的 \(s,t\) 判断你有没有必胜策略。
把当前状态设为点 \((x,v)\),其中 \(x\) 为当前在序列的哪个位置,\(v\) 为当前状态下格子里的值,\((x,v)\) 就能走到 \((x+1,a_{x+1})\) 和 \((x,v-1)\)(前提是 \(v>0\)),显然 \(SG(t,0)=0\),显然递归求出 \(SG(s,a_{s})\) 就能得出答案。拿到了这一档的部分分!非常的机动。
然后想一想就可以发现我们是把 \(t\) 的结果往前倒推的,尝试从 \(a_{t}\) 出发。发现用 \(1\) 表示当前状态的 \(SG>0\),\(0\) 表示等于 \(0\),发现 \((t,a_{t})\) 的 \(SG\) 恰好是 a[t]&1。然后发现每一个点的 \(SG\) 值只与最多向后 \(k\) 个位置原值对应的 \(SG\) 值有关,如果一个位置的 \(SG\) 为 \(0\),那么向前 \(k\) 位都会是 \(1\),如果一个位置是 \(1\),那么它的下一位就是 a[x]&1。所以令人机动地发现这就变成了一个 \(01\) 序列上往前跳的问题!然后又注意到只需要记录每个位置的奇偶性,卡一卡就拿到了 \(40pts\) 的高分!
这个时候我已经机动了,然后推了一个错误的结论之 s 向前 k 步之内有 0 就能过!写了神秘线段树交上去获得了 \(0\) 分的好成绩!
正解是分块。
晚上 abc403. 6题,青了。类目了。写到一半刘老师过来说 g 是线段树板子,一看榜玛雅隔壁都有人过了,那我对着这个 dp 调了一万年显得我很呆。交完这题时间已经不够写 g 了。就这样吧。还没人家分高。泪流满面了。

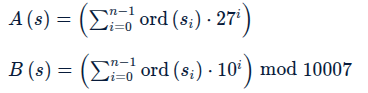

 浙公网安备 33010602011771号
浙公网安备 33010602011771号