Shell排序（改良的插入排序）
Shell排序算法最初是由D.L Shell于1959年提出，假设要排序的元素有n个，则每个进行插入排序是并不是所偶的元素同时进行，而是去一段间隔。
Shell首先将间隔设定为n/2，然后跳跃的进行插入排序，再来将间隔设定为n/4，跳跃进行排序动作，再来设定时间间隔为n/8、n/16，知道间隔为1之后的最后一次排序终止，由于上一次的排序动作都会将固定间隔内的元素排序好，所以当间隔为1之后的最后一次排序终止，由于上一次的排序动作都会将固定间隔内的元素排序好，所以当间隔越来越小时，某些元素位于正确位置的几率越高，因此最后几次的排序动作将可以大幅减低。
举个例子来说，假如有一未排序的数字如右：89 12 65 97 61 81 27 2 61 98
数字的总数共有10个，所以第一次我们将间隔设定为10/2=5，此时我们对间隔为5的数字进行排序，如下所示：
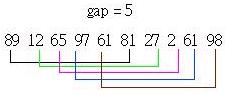
总结连线的部分表示要一起进行排序的部分，再来将间隔设定为5/2的商，也就是2，则第二次的插入排序对象如下所示：
再来间隔设定为2/2=1，此时就是单纯的插入排序了，由于大部分的元素都已大致排序过了，所以最后一次的插入排序机会没有什么排序动作了：
将间隔设定为n/2是D.L Shell最初所提出，在教科书中使用这个间隔比较好说明，然而Shell排序法的关键在于间隔的设定，例如Sedgewick证明选用以下的间隔可以加快Shell排序算法的速度：
其中4*(2j)2 + 3*(2j) + 1不可超过元素总数n值，使用上式找出j后代入4*(2j)2 + 3*(2j) + 1求得第一个间隔，然后将2j除以2代入求得第二个间隔，再来依次类推。
后来还有人证明有其它的间隔选定方法可以将Shell排序算法的速度再加快；另外Shell排序算法的概念也可以用来改良冒泡排序算法。
C#实例：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
private static void ShellSort(){ int[]
num = new int[]
{ 70, 80, 31, 37, 10, 11, 48, 60, 33, 80 }; int length
= num.Length; int gap
= length / 2; WriteNumLine(num); while (gap
> 0) { for (int k
= 0; k < gap; k++) { for (int i
= k + gap; i < length; i += gap) { for (int j
= i - gap; j >= k; j -= gap) { if (num[j]
> num[j + gap]) { int temp
= num[j + gap]; num[j
+ gap] = num[j]; num[j]
= temp; } else { break; } } } } gap
= gap / 2; WriteNumLine(num); } WriteNumLine(num);}private static void WriteNumLine(int[]
num){ foreach (int i in num) { Console.Write(i
+ "
"); } Console.WriteLine();} |
