题解：P10678

题面

P10678

![[../../题面/洛谷题面/P10678|P10678]]

分析

设树集 \(T\),构造树集 \(T'\),树节点树 \(n\),根节点 \(R\),且树集 \(T'\) 的每个叶子结点的深度 \(l_j\),最深节点深度 \(l_{max}\),非严格次深节点深度 \(l_{max}'\),树的直径子集 \(T_h\),树的直径长 \(h\).

求树的最小的两节点之间最大距离 \(\text{diam}({T'})\) 等价于最小的构造树 \(T'\) 的直径长即

\[\text{diam}(T')=h_{min}=l_{max}+l'_{max} \]

有 \(h_{min}\le 2l_{max}\), \(R\in T_h\in T'\)

给定树 \(T\) 每个节点度数 \(d_i\),求树最小直径深度 \(h_{min}\),显然每个节点的编号不影响树的构造,我们只要关心通过节点度数构造,由 \(h_{min}\le 2l_{max}\) 得需最小化构造树的最大深度.

由于节点总度数确认,树边要么使树"变深",要么使树"变宽",那么一旦建边优先使其"变宽"必然最小化 \(l_{max}\),可以理解成将所有的点及其子树尽可能向上移,也就是让入度大的点尽可能上移.

那么将点入度从大到小排序,那么根节点取入度最大点,每次建边都取剩余的入度最大的点.

具体实现

用结构体 \(\text{vector}\) 模拟树,将每个元素的度数和原次序绑定,贪心取入度最大点建树

（改度数用出度,除了根节点之外的度数均减一为出度）

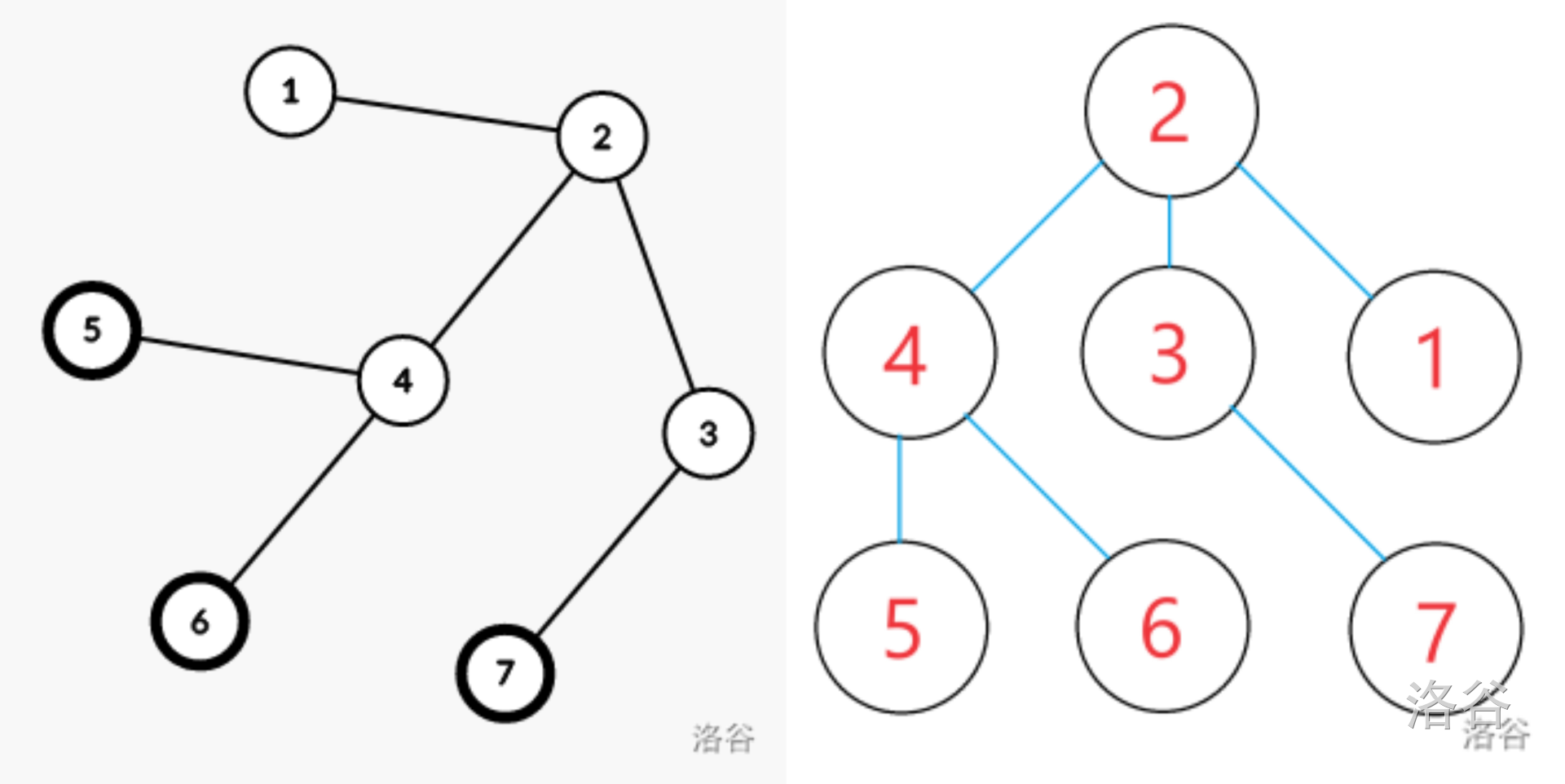
怕代码不方便理解,补个相当通俗的样例调试(如样例 \(4\) ):

7
1 3 2 3 1 1 1

通过结构体将每个元素的度数和原次序绑定,得如下顺序：

//表格1
2 4 3 1 5 6 7
3 3 2 1 1 1 1

建树：

//表格2
2      //节点情况
4 3 1 
5 6 7 

3      //子节点数
2 1 0
0 0 0

附代码：

#include <bits/stdc++.h>
using namespace std;
#define to(x,y); for(int x=1;x<=y;x++)
#define fr(x,y); for(int x=0;x<y;x++)
const int N = 2e5 + 20;
int t, n, sum[N];

struct nd {
	int ord, cry;
} p[N];
vector<nd> tr[N];

bool cmp(nd a, nd b) {
	if (a.cry == b.cry)
		return a.ord < b.ord;
	return a.cry > b.cry;
}

int main() {
	scanf("%d", &t);
	while (t--) {
		scanf("%d", &n);
		to(i, n)scanf("%d", &p[i].cry), p[i].ord = i;
		sort(p + 1, p + 1 + n, cmp);
		to(i, n) {
			if (i > 1)
				p[i].cry--;
			sum[i] = sum[i - 1] + p[i].cry;
		}
		int l = 1, r = 1, num, dep = 1;
		tr[1].push_back({p[1].ord, p[1].cry});
		while (r < n) {
			dep++;
			num = sum[r] - sum[l - 1];
			l = r + 1, r = r + num;
			for (int i = l; i <= r; i++)
				tr[dep].push_back({p[i].ord, p[i].cry});
		}
		to(i, dep - 1) {
			int len = tr[i].size(), idx = 0;
			fr(j, len) {
				for (int k = 0; k < tr[i][j].cry; k++) {
					printf("%d %d\n", tr[i][j].ord, tr[i + 1][idx + k].ord);
				}
				idx += tr[i][j].cry;
			}
		}
		to(i, dep)vector <nd>().swap(tr[i]);
	}

	return 0;
}

---

再附带有上面表格可视化输出并附解释的完整版：

#include <bits/stdc++.h>
using namespace std;
#define to(x,y); for(int x=1;x<=y;x++) //丑陋的代码化简习惯
#define fr(x,y); for(int x=0;x<y;x++)
const int N = 2e5 + 20;
int t, n, sum[N];

// sum 为出度前缀和,求每层的节点数
struct nd {
	int ord, cry;//ord序号,cry度数
} p[N];          //存输入数据并做预处理用
vector<nd> tr[N];//核心 vector 树

bool cmp(nd a, nd b) {
	if (a.cry == b.cry)
		return a.ord < b.ord;
	return a.cry > b.cry;
}//排序预处理

int main() {
	scanf("%d", &t);
	while (t--) {
		scanf("%d", &n);
		to(i, n)scanf("%d", &p[i].cry), p[i].ord = i;
		sort(p + 1, p + 1 + n, cmp)；
		
		
		
		/*表格一*/
//		puts("\n&&&");
//		to(i, n)printf("%d ", p[i].ord);
//		puts("");
//		to(i, n)printf("%d ", p[i].cry);
//		puts("\n&&&\n");
		
		
		
		to(i, n) {
			if (i > 1)
				p[i].cry--;//改度数为出度
			sum[i] = sum[i - 1] + p[i].cry;//算每层节点数
		}
		int l = 1, r = 1, num, dep = 1;
		tr[1].push_back({p[1].ord, p[1].cry});//存下根节点
		while (r < n) {
			dep++;//由上一层来到下一层
			num = sum[r] - sum[l - 1];//上层度数之和
			l = r + 1, r = r + num;
			for (int i = l; i <= r; i++)//“领养”子节点
				tr[dep].push_back({p[i].ord, p[i].cry});//存下该层子节点
		}
		
		
		
		/*表格二*/
//		to(i, dep) {
//			printf("&&&");
//			int len = tr[i].size();
//			fr(j, len)printf("%d ", tr[i][j].ord);
//			puts("&&&");
//		}
//		puts("");
//		to(i, dep) {
//			printf("&&&");
//			int len = tr[i].size();
//			fr(j, len)printf("%d ", tr[i][j].cry);
//			puts("&&&");
//		}
		
		
		
		to(i, dep - 1) {
			int len = tr[i].size(), idx = 0;
			// idx 为待领养子节点
			fr(j, len) {
				for (int k = 0; k < tr[i][j].cry; k++) {
					printf("%d %d\n", tr[i][j].ord, tr[i + 1][idx + k].ord);
				}//输出父子
				idx += tr[i][j].cry;//领下一批子节点
			}
		}
		to(i, dep)vector <nd>().swap(tr[i]);
		//清空 vector 树
	}
	return 0;//完结撒花🌸
}