映射

映射

基本概念

1. 概念：映射是集合与集合间的对应关系。

2. 定义：设 \(A\) , \(B\) 为非空集，若存在对应法则 \(f\) ，使得对每个 \(x \in A\) 都有唯一确定的 \(y \in B\) 与之对应，则称对应法则 \(f\) 为从 \(A\) 到 \(B\) 的映射。

3. 一般记为 \(f : A \to B\) ，其表达形式为 \(y = f(x),x \in A,y\in B\) 。

4. 严格地，记做 \(\forall x\in A,\exists !y\in B:y=f(x)\) (单值映射)。

5. 其中每项各记作：

   1. \(A\) 称为映射 \(f\) 的定义域，记为 \(D_f\) ；
   2. \(y\) 称为元素 \(x\) 在映射 \(f\) 下的像，记做 \(f(x)\) ；
   3. \(f(x)\)的集合 称为映射 \(f\) 的值域，记做 \(R_f\) (**注意! \(B\) 不一定等于 \(R_f\) **)

一般地，一个自变量仅对应一个因变量，称为单值映射；特殊地，若一个自变量对应多个因变量，称为集值映射。不引起歧义下后续映射均指单值映射。

类型

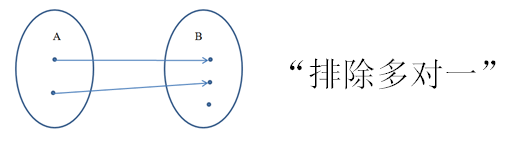
1. 单射：若 \(\forall x1,x2\in A且x1\neq x2\) ，有 \(f(x1)\neq f(x2)\) ，则称 \(f\) 为单射。
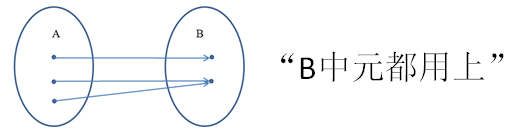
2. 满射：若 \(f(A)=B\) ，即 \(\forall y\in B,\exists x\in A\) 使得 \(f(x)=y\) ，则称 \(f\) 为满射。
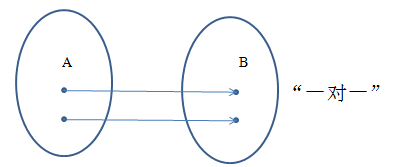
3. 双射：单且满的映射 \(f\) 称为双射。
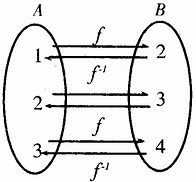
4. 逆映射:对于双射 \(f:A\to B\) 若存在 \(f^{-1}:B\to A\) ，则称 \(f^{-1}\) 为 \(f\) 的逆映射。
5. 复合映射：设映射 \(g:A\to B_1,f:b_2\) 若 \(B_1\subseteq B_2\) ，则对每个 \(x\in A\) ，都有唯一确定的 \(y\in C\) 满足 \(y=f(g(x))\) ，该对应法则就确定了一个映射 \(f\circ g:A\to C\) 称为 \(f\) 和 \(g\) 的复合映射，其表达式为 \((f\circ g)(x)=f(g(x)),x\in A\) (注意！可构成复合映射的条件是 \(R(g)\subset D(f)\) )。
6. 集值映射：(拓扑学和泛函分析中的基本概念)设 \(p(B)\) 表示 \(B\) 的所有子集构成的集族，称映射 \(f:A\to p(B)\) 为从 \(A\) 到 \(p(B)\) 的一个集值映射。
7. 集合映射：映射的像(函数值)是集合，与集值映射的区别在于在形式上，把映射的像用集合封装，可视为集值映射的严格数学表达。
8. 模糊映射：过超纲，略。
9. 随机映射：映射的像有关熵池的熵值，具有随机性。(资料较少，此定义不一定严格，该映射也极可能不是一个严格的映射关系)
10. 函数：对映射 \(f:A\to B\) ，若 \(A,B\) 都是数集，称为函数。
11. 反函数：对双射函数 \(f:A\to B\) ，其逆映射 \(f^{-1}:B\to A\) 称为该函数的反函数。(双射等价于改成 \(f:D\to f(D)\) 为单射，因为右端的 \(f(D)\) 隐含了该映射为满射)。
12. 变换：一般习惯称 \(f:A\to A\) 这样原集合跟目标集合一样的映射为变换，如函数的平移等。
13. 恒等变换：变换中形如 \(f(a)=a\quad(=f^{-1}(a))\) 被称作恒等变换，一般记作 \((\forall a\in A):id_A(a)=a\)

感性理解

前言：我所采用的激进理解是基于已学知识的既视感产生联想。每个人在保证最基本的理解符号间不产生较大冲突的前提下，可以去孕育自己的感性理解内容。

映射不应该是狭义死板的，他作为描述变化的工具应该具有通用性。不仅仅是函数中自变量到函数值的式子，也可以描述函数的平移，像 \(y=f(x)\rightarrow y=f(x-5)+3\) 这样对函数进行右移 \(5\) 单位，上移 \(3\) 单位的就可以写成：

\[g(\boxed{f(x)})=\boxed{f(x-5)+3} \]

甚至魔怔一点，写成这样也不妨

\[\boxed{(x,y)}\xmapsto{g}\boxed{(x-5,y+3)} \]

也就是将映射看做

\[\boxed{a}\xmapsto{f}\boxed{f(a)} \]

在函数板块的平移专栏中，我们将运用这种直观的写法

很多人不理解映射的原因，是纠结映射到底实在描述和强调的是 \(\boxed{集合之间的关系}\) 还是 \(\boxed{令变量 a 变成 f(a) 的式子}\) ？

前者其实是宏观的，后者其实是微观的，我一般认为是前者，毕竟定义便在强调这一点。也就是我们说这种关系是映射关系，而不是说这个式子是个映射，比如 \(f(a)=a^2\) 是函数(映射)，但 \(a^2\) 不是，前者是蕴含着 \(\boxed{关系}\) 这层含义的。

我们平时学习中都在考虑怎么去构造这个式子，很少讨论过自变量和映射值的关系。忽略了具体关系，很可能会使你在构造复合函数时出错，请注意到在上面复合函数的定义中，对集合间定义域和值域的关系是有要求的。

还有一个重要的点是，不要拿函数的思维去看映射，函数是映射的一种，但每种映射的性质不同。函数有的性质，别的映射不一定有，大部分函数都不是单射映射，我们一般认为函数值域是都能映射取到的，这会加大你理解单射的难度。

(如果你愿意跟我一起抽象，你可以把这个 \(f\) 看做所有是：\(\boxed{所有实现这样的关系的函数式的集合}\) ，讨论他们共同的性质就好)

1. 单射：

不存在多个自变量的映射值相同

2. 满射

所有自变量的映射值的集合等于定义域

3. 双射

两集合每个值都能在另一集合中找到有且仅有一个值与其对应

4. 逆映射和反函数

这里有个感性理解，我们可以把正常的映射式中 \(f(a)=b\) 直接看成 \(f\times a=b\) (这里的乘号是抽象性质的乘号)，那么便有

\[a=\frac{b}{f}=b \times f^{-1} \implies f^{-1}(b)=a\implies f^{-1}:B\to A \]

5. 复合函数

易于理解，如图

6. 集值映射和集合映射

由于一些习惯原因吧，一般人们认为映射的映射值仅有一个，但是如 \(f(正偶数)=\{2,4,...,2048\}=\{x\vert x=2y,y\in N^+\}\) 这样的映射实际是多个映射值的，称为集值映射或多值映射。

当然有的人不愿意这么看，希望更严格地定义这种映射关系，而将所有映射值聚为集合，认为映射的输出值实际是一个集合而非一堆元素这样更严格地定义。

我认为两种说法在一般情况下不影响，均可。

(暂时找不到图片)

7. 随机映射

映射值不定的映射，如 \(rand(l,r)\) 为区间 \([l,r]\) 的随机数

8. 变换和恒等变换

前言：变换只是源集合与目标集合一样的映射的习惯叫法，很多人依旧称其为映射和恒等映射。

感性理解的顶上的那个函数值的平移，就是从函数集映射到函数集，经典的变换。

还有我们的三角函数中 \(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\) ，还有极化恒等式 \(\overrightarrow{a}+\overrightarrow{b}=(\frac{\overrightarrow{a}+\overrightarrow{b}}{2})^2-(\frac{\overrightarrow{a}-\overrightarrow{b}}{2})^2\) 都是经典的恒等变换。