优化学习率相关算法

优化学习率的相关算法

在使用优化算法的时候，常常会涉及到一些学习率的优化，那么我们应该怎么优化学习率呢？

调整学习率的策略：

1.在斜率(方向导数)大的地方，使用小的学习率

2.在斜率(方向导数)小的地方，使用大的学习率

下面我们通过梯度下降算法进行学习率的优化分析

在梯度下降中，设x[k]=a，那么沿着负梯度方向，移动到x[k+1]=b,则有：

 那么，从x[0]出发，每次沿着当前函数梯度反方向移动一定的距离ak，将得到下面的序列：

 则对应的个点的函数值序列的关系为：

 当n迭代到一定值的时候，这函数f(x)将收敛到局部的最小值。

我们将当前点记为x[k]，当前的搜索方向为dk(如：负梯度方向)，我们将学习率a看成自变量，因此，我们将函数f(x[k] + adk)看做是关于a的函数h(a)，如下所示：

 对于上述函数，当a=0时，h(0)=f(x[k])，对于函数h(a)，其导数为：

 在梯度下降中，梯度下降是为了寻找f(x)的最小值，那么，在x[k]和dk给定的前提下，即寻找函数f(x[k]+adk)的最小值， 即：

 如果函数h(a)可导，那么对于局部最小值处的a满足：

 下面我们就来计算最优学习率：

1.当a=0时，我们带入得到：

 2.对于下降方向，选择负梯度方向(或者选择与负梯度方向夹角小于90度的方向)，即：

 可以得到h‘(a) < 0

 3.由此，我们总是能够选择足够大的a，使得h'(a) > 0，这样，就一定存在某a，使得h'(a) = 0，此时的a即为要寻找的a值。

接下来我们可以采用多种方法计算a值：

1.线性搜索

最简单的方式就是采用二分线性搜索的方式，通过不断的将区间[a1，a2]分成两半，选择端点异号的区间，当区间分的足够小的时候，我们就能得到一个足够好的最优学习率。

2.回溯线性搜索

 我们还可以采用基于Armijo准则计算搜索方向上的最大步长，其基本思想是沿着搜索方向移动一个较大的步长估计值，然后以迭代形式不断缩减步长，直到该步长使得函数值f(xk+αdk)相对与当前函数值f(xk)的减小程度大于预设的期望值(即满足Armijo准则)为止。

 

 两种方法的异同：

二分线性搜索的目标是求得满足h‘(α)≈0的最优步长近似值，而回溯线性搜索放松了对步长的约束，只要步长能使函数值有足够大的变化即可。

二分线性搜索可以减少下降次数，但在计算最优步长上花费了不少代价；回溯线性搜索找到一个差不多的步长即可。

回溯线性搜索的思考：插值法

采用多项式插值法(Interpolation) 拟合简单函数，然后根据该简单函数估计函数的极值点，这样选择合适步长的效率会高很多。现在拥有的数据为： xk处的函数值f(xk)及其导数f’(xk) ，再加上第一次尝试的步长α0。如果α0满足条件，显然算法退出；若α0不满足条件，则根据上述信息可以构造一个二次近似函数：

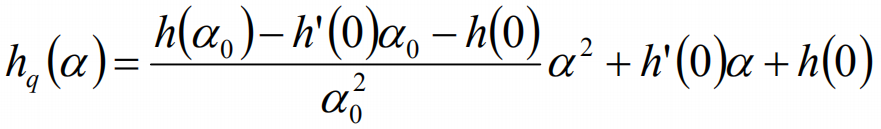
 这样，我们可以计算导数为0的最优值。

一般的说，回溯线性搜索和二次插值线性搜索能够基本满足实践中的需要。