排序算法-3-堆排序

一. 基本介绍

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树（左边可能大于右边）的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法：

1. 大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；
2. 小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

堆排序的平均时间复杂度为 Ο(nlogn)。

 

二. 算法步骤

1. 先创建一个堆

2. 将堆头与堆尾调换

3. 将堆尺寸缩小，并重新调整

4. 重复步骤2，3。直到堆的尺寸呢为1

 

三. 图解

 

 

 

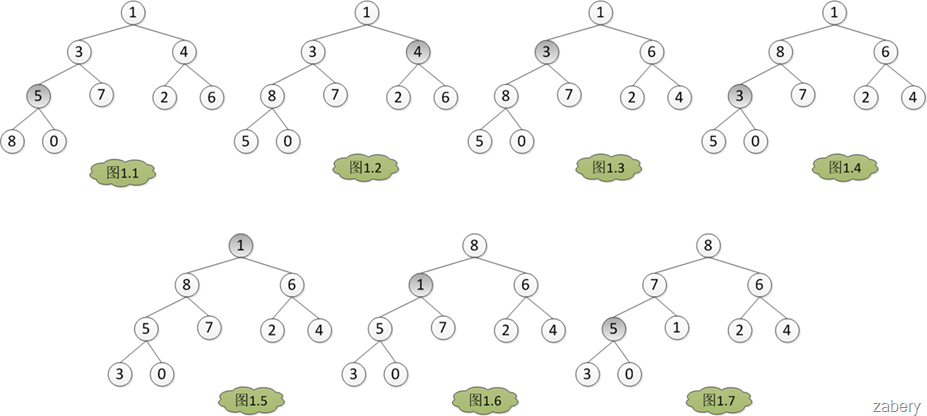
四. 源码

void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

void max_heapify(int arr[], int start, int end) {
    int dad = start;
    int son = dad * 2 + 1;
    while (son <= end) {
        if (son + 1 <= end && arr[son]<arr[son+1]) {
            son++;
        }
        if (arr[dad] > arr[son]) { 　　//对于调整完毕的部分来说，dad总是大于son的，因此不必关心孙结点的情况，只要满足这个，就可以退出
            return;
        }
        else {
            swap(&arr[dad], &arr[son]);    
            dad = son;
            son = son * 2 + 1;
        }
    }
}

void heapSort(int arr[], int len) {
    int i;
    // 初始化，i从最后一个父结点开始调整
    for (i = len / 2 - 1; i >= 0; i--)
        max_heapify(arr, i, len - 1);
    // 先将第一个元素（因为它总是最大的）和已排好元素前一位做交换，再重新调整，直到排序完成
    for (i = len - 1; i > 0; i--) {
        swap(&arr[0], &arr[i]);
        max_heapify(arr, 0, i - 1);
    }
}