二叉树中的递归算法（二）

从二叉树遍历看递归

• 二叉树
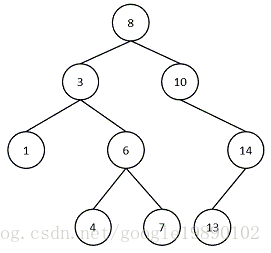
  二叉树（binary tree）是指树中节点的度不大于2的有序树，它是一种最简单且最重要的树。 二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树。
  

二叉树的遍历

• 注意 ：
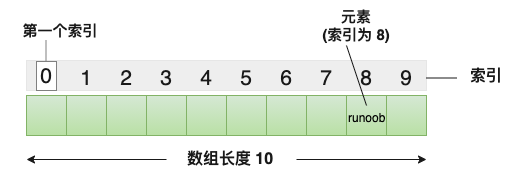
  1、在遍历数组时我们发现只有一种遍历的策略就是随着 index -> 的递增进行遍历
  
  2、依据第一条，我们在使用递归算法进行数组遍历时也只有一种选择的策略

    public static void traverseArray(int index) {
        if (index == LEN) {
            System.out.println();
            // 递归边界无论有没有返回值都需要进行 return;
            return;
        }
        System.out.printf("%d " , array[index]);
        traverseArray(index + 1);
    }

---

• 遍历
  1、二叉树在使用递归算法进行遍历时，由于有两条路径所以有两种向前策略

void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    // 前序位置 
    traverse(root.left); // 路径一
    // 中序位置
    traverse(root.right); // 路劲二
    // 后序位置
}

• 注意这是有两条遍历路径的情况，那么如果有多条路径了

void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    for (TreeNode each : root.children) {
      traverse(each );
    }
}

注意：在使用递归算法时，如果需要进行数据的响应计算需要把数据进行复原，也就是说在前序逻辑时增加了一个，在后续逻辑处就需要减少一个。
1、包括在递归算法中使用的额外变量

int path[N];
bool st[N];
void dfs(int u) {
    if (u == n) {
        for (int i = 0 ; i < n ; i ++ ) printf("%d ",path[i]);
        printf("\n");
        
        return;
    }
    else {
        for (int i = 1 ; i <= n ; i ++ ) {
            if (!st[i]) {
                // 数据使用情况记录
                st[i] = true;
                path[u] = i;
                dfs(u + 1);
                // 在后续遍历位置进行数据还原，因为在新的一轮遍历中不需要使用前面一次遍历路径中使用的数据。如果不还原会导致脏数据的出现
                st[i] = false;
            }
        }
        
    }
}