排序算法

首先定义一个交换数组元素的方法，对于给定数组int arr[], 交换i位置跟j位置的元素可以用一下方法实现

void Swap(int[] arr, int i, int j)
{
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

选择排序: 每次选择最小的元素跟未排序序列的第一个元素交换

public class Selection
{
    public static void Sort(int[] arr)
    {
        for (int i = 0; i < arr.Length; i++)
        {
            int minIndex = i;
            for (int j = i + 1; j < arr.Length; j++)
            {
                if (arr[j] < arr[minIndex])
                    minIndex = j;
            }
            Swap(arr, i, minIndex);
        }
    }
}

 

插入排序: 扫描整个数组，将每个元素都插入到适当的位置，当前元素左边的所有元素都是有序的，但最终位置还不固定，当遍历完整个数组，所有元素都是有序的

public class Insertion
{
    public static void Sort(int[] arr)
    {
        for (int i = 1; i < arr.Length; i++)
        {
            for (int j = i; j > 0 && arr[j] < arr[j - 1]; j--)
            {
　　　　　　　　　　Swap(arr, j, j-1);
            }
        }
    }
}

希尔排序: 希尔排序是基于插入排序的一种改进，将下标按一定增量进行分组，对每组元素使用直接插入排序，当增量减至1时，整个数组就变成有序的

 

 

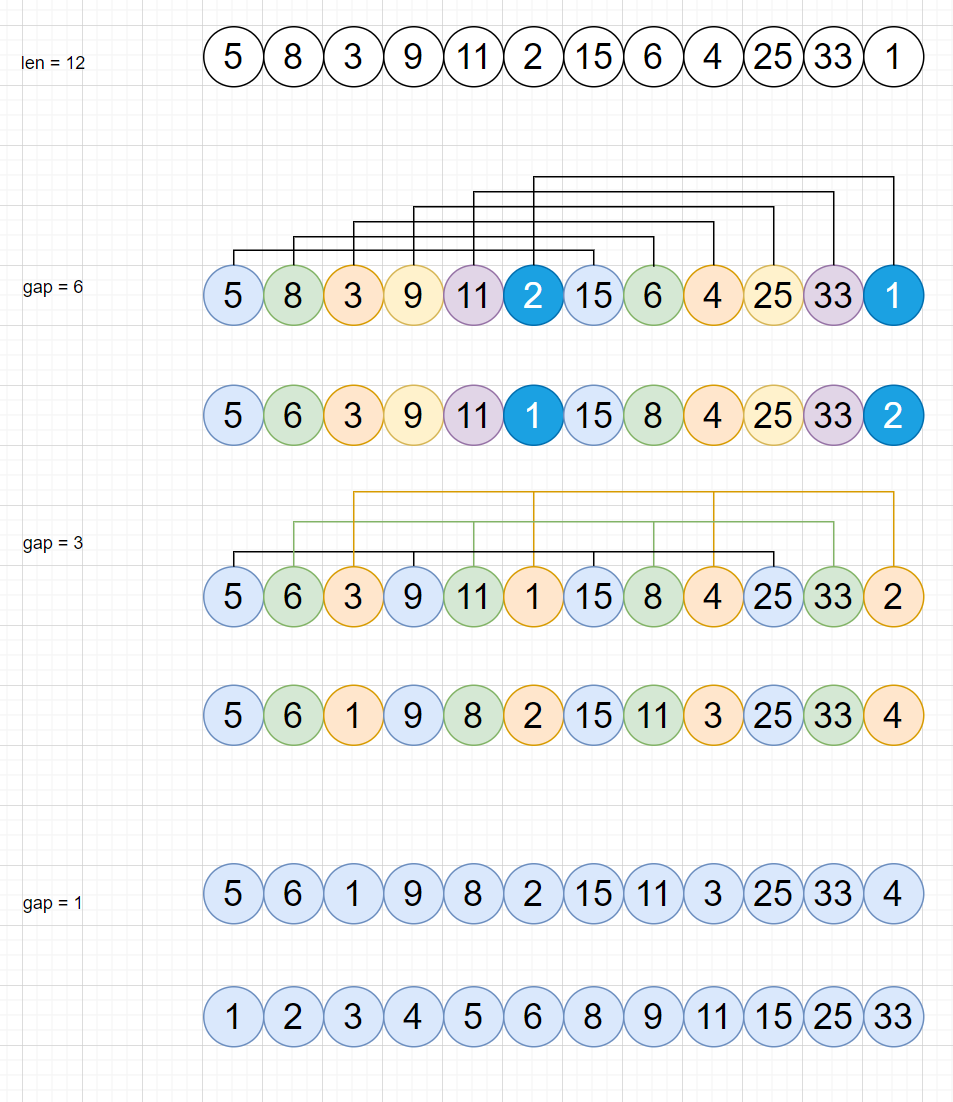
public class Shell
{
    public static void Sort(int[] arr)
    {
        for (int gap = arr.Length / 2; gap > 0; gap /= 2)
        {
            for (int i = gap; i < arr.Length; i++)
            {
                int j = i;
                while (j - gap >= 0 && arr[j] < arr[j - gap])
                {
                    Swap(arr, j, j - gap);
                    j -= gap;
                }
            }
        }
    }
}

 归并排序: 递归的将一个数组分成两部分，分别排序之后再将结果合并起来，整个数组就做到了有序

public class MergeSort
{
    public static void Sort(int[] arr, int begin, int end)
    {
        if (begin < end)
        {
            var mid = (begin + end) / 2;
            Sort(arr, begin, mid);
            Sort(arr, mid + 1, end);
            Merge(arr, begin, mid, end);
        }
    }

    public static void Merge(int[] arr, int L, int mid, int R)
    {
        int[] help = new int[R - L + 1];
        int i = 0;
        int p1 = L;
        int p2 = mid + 1;
        
        while (p1 <= mid && p2 <= R)
        {
            help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
        }

        while (p1 <= mid)
        {
            help[i++] = arr[p1++];
        }

        while (p2 <= R)
        {
            help[i++] = arr[p2++];
        }

        for (int j = L; j <= R; j++)
        {
            arr[j] = help[j - L];
        }
    }
}

快速排序：选取一个元素对整个数据进行Partition，将小于该元素的放左边，大于该元素的放右边，再递归对左右两部分重复操作，最终完成整个数组的排序

下面的实现针对重复元素做了优化，Partition试采用3分法

 

 

 

 

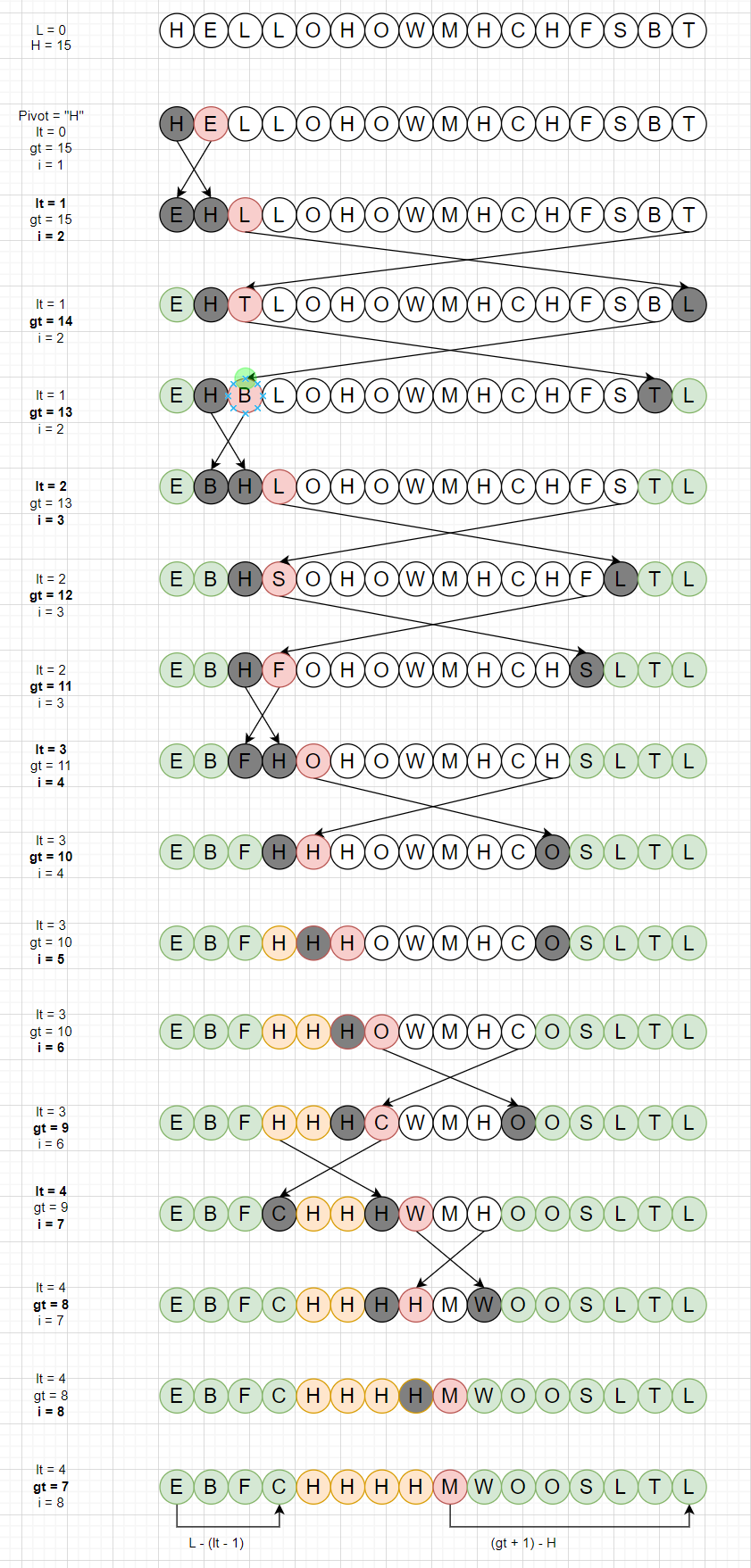
public class QuickSortV2
{
    public static void Sort(int[] arr, int L, int H)
    {
        if (L >= H)
            return;

        int lt = L;
        int gt = H;
        int i = L + 1;
        int pivot = arr[L];
        while (i <= gt)
        {
            if (arr[i] < pivot)
            {
                Swap(arr, i++, lt++);
            }
            else if (arr[i] > pivot)
            {
                Swap(arr, i, gt--);
            }
            else
            {
                i++;
            }
        }

        Sort(arr, L, lt - 1);
        Sort(arr, gt + 1, H);
    }
}

 堆排序: 将输入元素构造成一个大根堆，不断删除堆顶元素，并维持大根堆结构，最终所有元素将按照从小到大的顺序排列

public class HeapSort
{
    public static void Sort(int[] arr)
    {
        if (arr == null || arr.Length < 2)
            return;

        for (int i = 0; i < arr.Length; i++)
        {
            HeapInsert(arr, i);
        }

        int heapSize = arr.Length;
        Swap(arr, 0, --heapSize);

        while (heapSize > 0)
        {
            Heapify(arr, 0, heapSize);
            Swap(arr, 0, --heapSize);
        }
    }
    
    public static void HeapInsert(int[] arr, int index)
    {
        while (arr[index] > arr[(index - 1) / 2])
        {
            Swap(arr, index, (index - 1) / 2);
            index = (index - 1) / 2;
        }
    }

    public static void Heapify(int[] arr, int index, int heapSize)
    {
        int left = index * 2 + 1;
        while (left < heapSize)
        {
            //更大孩子的索引
            int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1: left;

            largest = arr[largest] > arr[index] ? largest : index;

            if (index == largest)
                break;

            Swap(arr, index, largest);
            index = largest;
            left = index * 2 + 1;
        }
    }
}

 总结：

算法	是否稳定	时间复杂度	空间复杂度
选择排序	否	N^2	O(1)
插入排序	是	N^2	O(1)
希尔排序	否	介于N ~ N^2	O(1)
归并排序	是	N*logN	O(N)
快速排序	否	N*logN	O(lgN)
堆排序	否	N*logN	O(1)