canvas 2d 贴图技术实践
最近在公司内部的技术协会论坛里闲逛的时候,无意中发现了一篇手淘前端大牛岑安两年前写的博文,讲述了canvas的2d贴图技术。看到后觉得相当神奇。于是就自己实现了一下。不过岑安前辈的那篇博文也只是大概讲述了一下实现思路,整个逻辑还是自己慢慢摸索出来的,过程还是挺心酸的,所以在此记录一下并且分享一下,让跟我一样喜欢canvas的人有所收获吧。
废话不说,先把demo贴出来,好歹让大伙看看我们要实现怎样的效果:
第一个demo: 图像拉扯变形demo_1
第二个demo: 图像3d变形demo_2
看完demo,是否觉得挺好玩的?
如果觉得好玩,那就继续看下去吧,接下来我将逐步分析整个实现逻辑。主要讲的就是第一个demo的实现逻辑,因为第二个就是在第一个的基础上实现的,只要理解了第一个的原理,第二个就变得很简单了。
第一个demo中,实现了对图像的拉扯,涉及到这种变形的,首先想到的就是transform,没错,就是canvas的2d绘图API中的transform啦。transform方法中传入的abcdef六个值就是变换矩阵的参数。也就是说,我们可以通过修改这六个值来实现对图片的变形操作。
transform() 允许您缩放、旋转、移动并倾斜当前的环境。如果对transform不是很了解的,可以看这篇博文:http://yehao.diandian.com/post/2012-12-30/40046242001 里面讲的还是很详细的。
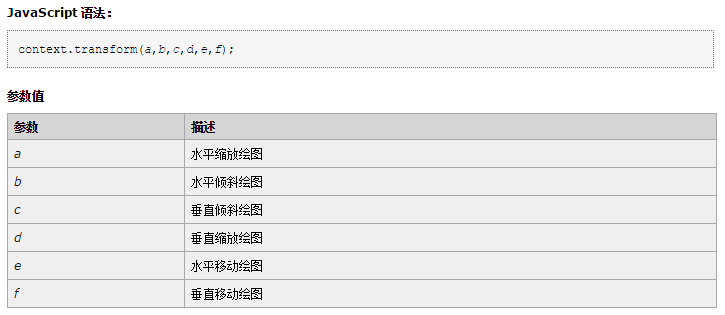
了解了transform之后,你会发现,transform能做的,好像就只有缩放、旋转、移动、倾斜这几个功能。但是demo1中可以拉扯成各种形状,感觉不像是用这几个就能实现的。但是其实,还真就是用这几个变换实现的。
demo1贴图右侧有个数值选择,当选择1,并且选择显示方框的时候,我们看到是这样一个画面:

没错,这个是什么意思呢,说明这张图片其实分成了两块,左上角的三角形以及右下角的三角形,我们拖动一下图片,再看一下效果:

为了方便理解,我加了辅助线,画了辅助线后,就变得很简单了,相当于分成了两块,上面正常的图片,一块是变成了由红色圈起来的,另一块则是变成了由黑色圈起来的,当用画笔补全后,两个三角形都其实是一个平行四边形,而从矩形变成平行四边形,transform就能做了,当变成我们需要的形状的时候,再通过canvas的clip方法,只截取一半的三角形,把两块三角形合并起来。就有了拉扯效果了。
而为了让拉扯效果更真实,就自然就需要使用更多的三角区域,当我把矩形分成20*20个小矩形,也就是20*20*2个三角形的时候,当鼠标拉扯时就出现了以下效果:

以上,就是demo1的整个理论逻辑。
接下来就讲代码该如何实现:
首先是图片的变形效果,也就是用transform,要传入矩阵参数,起初我是用向量来做的,但是做到后面发现向量做起来会有好多其他问题。比如:图片拉扯过度的时候,图片翻转就出问题了,等等。。。
所以最后,还是选择了用代数法来实现,也就是要解三元一次方程!!!!
为啥说是三元一次方程呢?因为按照transform的矩阵运算的规则
|a , b , 0|
[X,Y,1] = [x , y , 1] * |c , d , 0|
|e , f , 1|
解出来就是这样:X = ax + cy +e 和 Y = bx + dy + f , 也就是,新的坐标的XY值就等于旧的坐标的xy值进行一些运算后可以得到。
相对的,也就是说,只要我们知道了平行四边形三个顶点变换前后的坐标值,我们就可以算出abcdef六个矩阵参数,然后我们先用transform改变绘制环境,再把图片绘制到平行四边形变换前的位置,就可以绘制出相应的倾斜效果了。
所以,首先我们要封装出一个解三元一次方程以及获取矩阵参数的方法:
先是解三元一次方程的方法,具体原理我就不讲了,百度一下就知道了,或者有琢磨精神的可以自己亲自拿笔算一下:
/** * 解三元一次方程,需要传入三组方程参数 * @param arr1 第一组参数 * @param arr2 第二组参数 * @param arr3 第三组参数 * @returns {{x: number, y: number, z: number}} */ function equation(arr1 , arr2 , arr3){ var a1 = +arr1[0]; var b1 = +arr1[1]; var c1 = +arr1[2]; var d1 = +arr1[3]; var a2 = +arr2[0]; var b2 = +arr2[1]; var c2 = +arr2[2]; var d2 = +arr2[3]; var a3 = +arr3[0]; var b3 = +arr3[1]; var c3 = +arr3[2]; var d3 = +arr3[3]; //分离计算单元 var m1 = c1 - (b1 * c2 / b2); var m2 = c2 - (b2 * c3 / b3); var m3 = d2 - (b2 * d3 / b3); var m4 = a2 - (b2 * a3 / b3); var m5 = d1 - (b1 * d2 / b2); var m6 = a1 - (b1 * a2 / b2); //计算xyz var x = ((m1 / m2) * m3 - m5)/((m1 / m2) * m4 - m6); var z = (m3 - m4 * x) / m2; var y = (d1 - a1 * x - c1 * z) / b1; return { x : x, y : y, z : z } }
然后就是获取矩阵,其实就是将各个参数整理一下,传入解方程的方法中,进行处理:
/** * 根据变化前后的点坐标,计算矩阵 * @param arg_1 变化前坐标1 * @param _arg_1 变化后坐标1 * @param arg_2 变化前坐标2 * @param _arg_2 变化后坐标2 * @param arg_3 变化前坐标3 * @param _arg_3 变化后坐标3 * @returns {{a: number, b: number, c: number, d: number, e: number, f: number}} */ function getMatrix(arg_1 , _arg_1 , arg_2 , _arg_2 , arg_3 , _arg_3){ //传入x值解第一个方程 即 X = ax + cy + e 求ace //传入的四个参数,对应三元一次方程:ax+by+cz=d的四个参数:a、b、c、d,跟矩阵方程对比c为1 var arr1 = [arg_1.x , arg_1.y , 1 , _arg_1.x]; var arr2 = [arg_2.x , arg_2.y , 1 , _arg_2.x]; var arr3 = [arg_3.x , arg_3.y , 1 , _arg_3.x]; var result = equation(arr1 , arr2 , arr3); //传入y值解第二个方程 即 Y = bx + dy + f 求 bdf arr1[3] = _arg_1.y; arr2[3] = _arg_2.y; arr3[3] = _arg_3.y; var result2 = equation(arr1 , arr2 , arr3); //获得a、c、e var a = result.x; var c = result.y; var e = result.z; //获得b、d、f var b = result2.x; var d = result2.y; var f = result2.z; return { a : a, b : b, c : c, d : d, e : e, f : f }; }
计算完毕,就可以获取到六个矩阵参数了。
这两个计算看似简单,但是一不小心就容易出错,楼主之前做的时候就一直出错,一直不知道原因在哪,最后手动把三元一次方程解了一遍,才发现是某个参数错了。所以楼主把这两个计算封装了一下,以便以后再利用:
github地址:https://github.com/whxaxes/wheels/tree/master/matrix 有兴趣或者有需要的可以一用
回归正题,到了现在,我们就可以获取到所有的矩阵参数了,接下来要解决的问题,就是如何把任意四个点连线形成的四边形分成N份的逻辑了(注意:是任意四个点,因为拉升之后,四个点形成的坐标就不是矩形了)。这个就可以用向量来做了,用向量的话,计算量会小很多,对性能的提升也是很有帮助。
怎么实现呢,画个图就清晰了:

我们只需要获取到AD向量,以及BC向量,把两个向量N等分,然后用个循环,在每一等分上获取AB方向的向量,然后再进行N等分,再计算,就可以获取到所有的点了。因为用的是向量,所以我们完全不用考虑角度的问题,无论四边形的形状如何,只要我们有四个点的坐标,就可以计算出里面的所有点坐标。代码如下:
/** * 将abcd四边形分割成n的n次方份,获取n等分后的所有点坐标 * @param n 多少等分 * @param a a点坐标 * @param b b点坐标 * @param c c点坐标 * @param d d点坐标 * @returns {Array} */ function rectsplit(n , a , b , c , d){ //ad向量方向n等分 var ad_x = (d.x - a.x)/n; var ad_y = (d.y - a.y)/n; //bc向量方向n等分 var bc_x = (c.x - b.x)/n; var bc_y = (c.y - b.y)/n; var ndots = []; var x1, y1, x2, y2, ab_x, ab_y; //左边点递增,右边点递增,获取每一次递增后的新的向量,继续n等分,从而获取所有点坐标 for(var i=0;i<=n;i++){ //获得ad向量n等分后的坐标 x1 = a.x + ad_x * i; y1 = a.y + ad_y * i; //获得bc向量n等分后的坐标 x2 = b.x + bc_x * i; y2 = b.y + bc_y * i; for(var j=0;j<=n;j++){ //ab向量为:[x2 - x1 , y2 - y1],所以n等分后的增量为除于n ab_x = (x2 - x1)/n; ab_y = (y2 - y1)/n; ndots.push({ x: x1 + ab_x * j, y: y1 + ab_y * j }) } } return ndots; }
计算完毕,并且把点绘制到各个坐标上的时候,拖动四个顶点,就出现了以下效果,无论我的四个顶点位置如何变幻,都能保证所有点的位置不会错。

当这个也计算完毕,整个demo的制作就基本上完成了,然后就是进行图片的渲染了,接下来的逻辑就相当简单了,先是用上面的rectsplit方法把当前的四边形分成N份,并且获取所有坐标点,当然还需要直接获取初始四边形分成N份后的所有坐标点,不过这个是可以在刚开始的时候就初始化好,因为这个数值是不会变的,没必要重复计算。
两组点坐标获取到,然后传入方法里计算矩阵,以及进行clip处理,再把图片绘制上去,整个渲染过程就完成了。
/** * 画布渲染 */ function render(){ ctx.clearRect(0,0,canvas.width,canvas.height); var ndots = rectsplit(count, dots[0], dots[1], dots[2], dots[3]); ndots.forEach(function(d , i){ //获取四边形的四个点 var dot1 = ndots[i]; var dot2 = ndots[i + 1]; var dot3 = ndots[i + count + 2]; var dot4 = ndots[i + count + 1]; //获取初始四边形的四个点 var idot1 = idots[i]; var idot2 = idots[i + 1]; var idot3 = idots[i + count + 2]; var idot4 = idots[i + count + 1]; if (dot2 && dot3 && i%(count+1)<count){ //绘制三角形的下半部分 renderImage(idot3, dot3, idot2, dot2, idot4, dot4); //绘制三角形的上半部分 renderImage(idot1, dot1, idot2, dot2, idot4, dot4); } if(hasDot){ ctx.save(); ctx.fillStyle = "red"; ctx.fillRect(d.x-1 , d.y-1 , 2 , 2); ctx.save(); } }); } /** * 计算矩阵,同时渲染图片 * @param arg_1 * @param _arg_1 * @param arg_2 * @param _arg_2 * @param arg_3 * @param _arg_3 */ function renderImage(arg_1 , _arg_1 , arg_2 , _arg_2 , arg_3 , _arg_3){ ctx.save(); //根据变换后的坐标创建剪切区域 ctx.beginPath(); ctx.moveTo(_arg_1.x, _arg_1.y); ctx.lineTo(_arg_2.x, _arg_2.y); ctx.lineTo(_arg_3.x, _arg_3.y); ctx.closePath(); if(hasRect){ ctx.lineWidth = 2; ctx.strokeStyle = "red"; ctx.stroke(); } ctx.clip(); if(hasPic){ //传入变换前后的点坐标,计算变换矩阵 var result = matrix.getMatrix.apply(this , arguments); //变形 ctx.transform(result.a , result.b , result.c , result.d , result.e , result.f); //绘制图片 ctx.drawImage(img , idots[0].x , idots[0].y , img.width , img.height); } ctx.restore(); }
至此,demo1的整个理论原理以及代码逻辑都分析完毕,下面贴出该项目的github地址:
https://github.com/whxaxes/canvas-test/tree/gh-pages/src/Funny-demo/transform
当demo1做出来的时候,demo2也就很简单了,因为,只要我们知道四边形的各个点变换前后的坐标值,我们就可以让图片变形成任何我们想要的样子。
而上面的demo2就是在demo1的基础上,加入了z轴的影响,x,y轴都仅仅是平面上的,当加入了z轴以后,再将z轴的值映射到x,y轴上来,然后再进行图片变换,就有了demo2的效果。demo2的源码也在上面那个github地址上,里面的demo1.js就是demo1的,demo2.js就是demo2的逻辑。

至此,整个过程都讲述完了。感谢一阅。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号