【优先队列(堆)】左式堆类模板的实现
左式堆(leftist heap)像二叉堆那样也具有结构性和有序性。
左式堆和二叉堆唯一的区别是:左式堆不是理想平衡的(perfectly balanced),而实际上是趋向于非常的不平衡。
左式堆的性质
把任一节点X的零路径长 (null path length) npl (X) 定义为从X到一个不具有两个儿子的节点的最短路径的长。因此,具有0个或1个儿子的节点的npl为0,而 npl (nullptr) = -1。
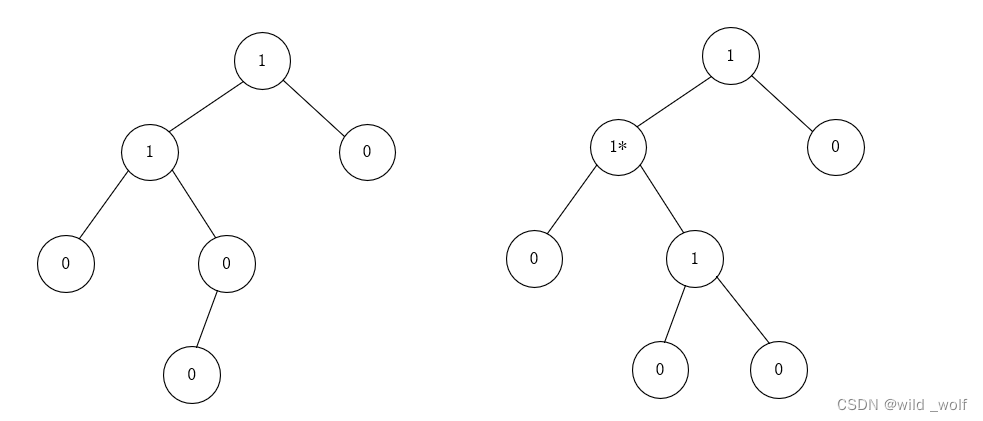
注意,任一节点的零路径长比它的诸儿子节点的零路径长的最小值多1。这个结论也适用少于两个儿子的节点,因为nullptr的零路径长是-1。
左式堆性质是:对于堆中的每一个节点X,左儿子的零路径长至少与右儿子的零路径长一样。图1中只有一棵树,即左边的那棵树满足该性质。这个性质实际上超出了它确保树不平衡的要求,因为它显然偏重于使树向左增加深度。确实有可能存在由左节点形成的长路径构成的树(而且实际上更便于合并操作)——因此,就有了名称左式堆。
在右路径上有 r 个节点的左式堆必然至少有 2r-1 个节点。
即,N个节点的左式堆有一条最多含有 ⌊log(N+1)⌋个节点的右路径。
左式堆操作
左式堆的基本操作是合并。插入只是合并的特殊情形,因为可以把插入看成是单节点堆与一个更大的堆的merge。
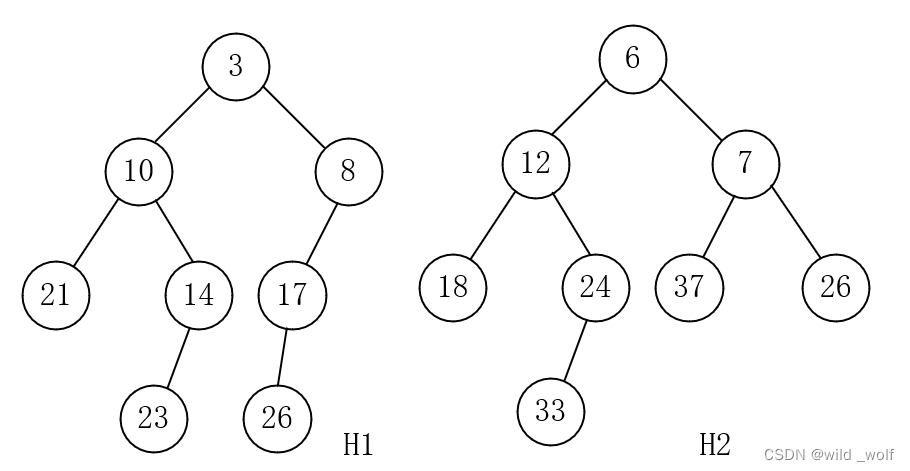
输入两个左式堆H1和H2。如果这其中有一个堆是空的,则可以返回另一个堆。否则,为合并这两个堆,应比较它们的根。首先,我们递归地将具有较大的根值的堆与具有较小的根值的堆的右子堆合并。
在本例中,我们递归地将H2与H1的根在8处的右子堆合并得到图3所示的堆。
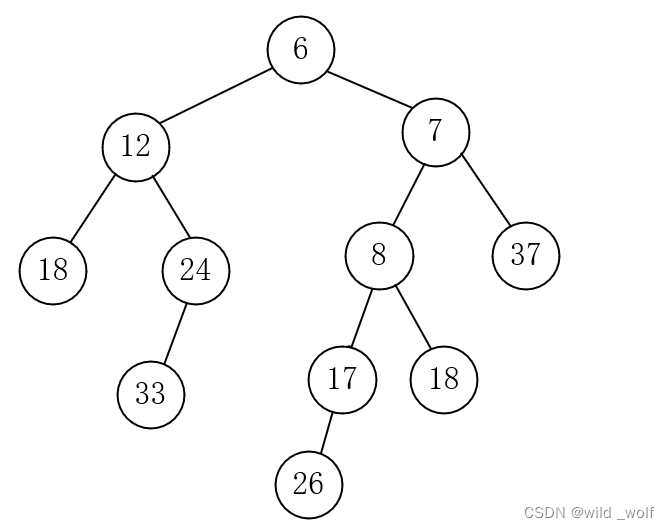
让这个新的堆成为H1的右儿子,
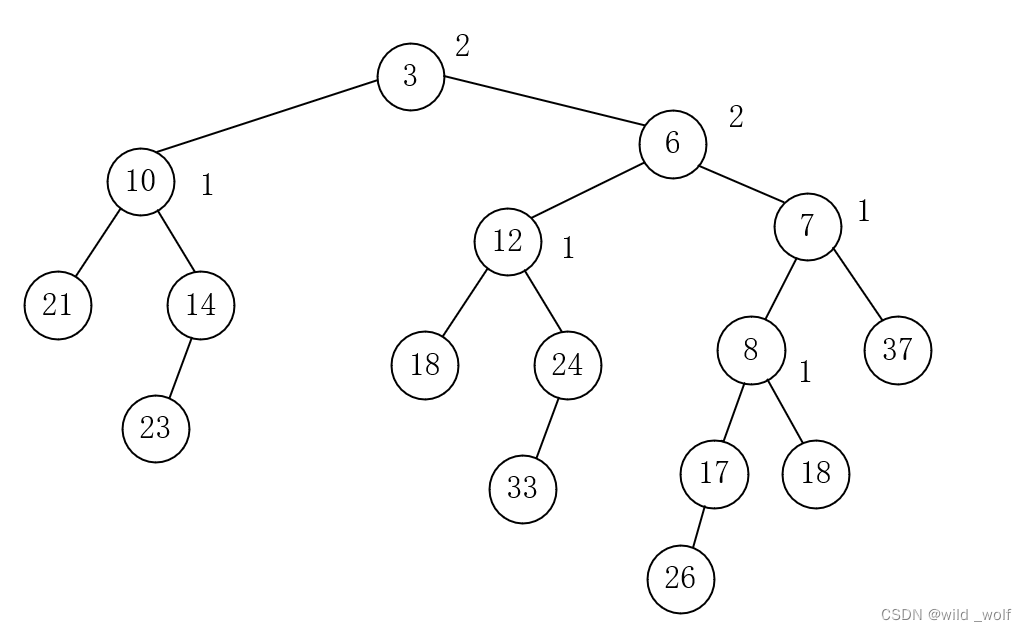
虽然得到的堆满足堆序性质,但它不是左式堆,因为根的左子树的零路径长为1而根的右子树的零路径长为2。因此需要调整根,使整个树是左式的做法如下:只要交换根的左儿子和右儿子并更新零路径长,就完成了merge,新的零路径长是新的右儿子的零路径长加1。
执行合并所用的时间与右路径的长的和成正比,因为在递归调用期间对每一个被访问的节点花费的是常数工作量。
实现代码
//左式堆类型声明
template<typename Comparable>
class LeftistHeap {
public:
LeftistHeap():root{nullptr}{}
LeftistHeap(const LeftistHeap& rhs) :root{ nullptr } {
root = clone(rhs.root);
}
LeftistHeap(LeftistHeap&& rhs) :root{ rhs.root } {
rhs.root = nullptr;
}
~LeftistHeap() { makeEmpty(); }
LeftistHeap& operator=(const LeftistHeap& rhs)
{
LeftistHeap copy = rhs;
std::swap(*this, copy);
return *this;
}
LeftistHeap& operator=(LeftistHeap&& rhs)
{
std::swap(root, rhs.root);
return *this;
}
bool isEmpty()const {
return root == nullptr;
}
/**
* 在优先队列中查找最小项
* 返回最小项,如果空为抛出异常
*/
const Comparable& findMin()const
{
if(isEmpty())
throw UnderflowException{};
return root->element;
}
/**
* 插入x,允许项重复
*/
void insert(const Comparable& x)
{
root = merge(new LeftisNode{ x }, root);
}
void insert(Comparable&& x)
{
root = merge(new LeftisNode{ std::move(x) }, root);
}
/**
* 删除最小项
* 若为空,则抛出异常UnderflowException
*/
void deleteMin()
{
if (isEmpty())
throw UnderflowException{};
LeftisNode* oldRoot = root;
root = merge(root->left, root->right);
delete oldRoot;
}
/**
* 删除最小项并将其放入minItem
* 若为空,则抛出异常UnderflowException
*/
void deleteMin(Comparable& minItem)
{
minItem = findMin();
deleteMin();
}
void makeEmpty() {
reclaimMemory(root);
root = nullptr;
}
/**
* 将rhs合并到优先队列
* rhs变为空,rhs必须不同于this
*/
void merge(LeftistHeap& rhs) {
if (this == &rhs) //避免别名问题
return;
root = merge(root, rhs.root);
rhs.root = nullptr;
}
private:
struct LeftisNode {
Comparable element;
LeftisNode* left;
LeftisNode* right;
int npl; //null path length,零路径长
LeftisNode(const Comparable&e,LeftisNode*lt=nullptr,LeftisNode*rt=nullptr,int np=0)
:element{e},left{lt},right{rt},npl{np}{}
LeftisNode(Comparable&& e, LeftisNode* lt = nullptr, LeftisNode* rt = nullptr, int np = 0)
:element{ std::move(e)}, left{lt}, right{rt}, npl{np}{}
};
LeftisNode* root;
/**
* 合并两个根的内部方法
* 处理不正常情形并调用递归的merge1
*/
LeftisNode* merge(LeftisNode* h1, LeftisNode* h2)
{
if (h1 == nullptr)
return h2;
if (h2 == nullptr)
return h1;
if (h1->element < h2->element)
return merge1(h1, h2);
else
return merge1(h2, h1);
}
/**
* 合并两个根的内部方法
* 假设树非空,并设h1的根包含最小项
*/
LeftisNode* merge1(LeftisNode* h1, LeftisNode* h2)
{
if (h1->left == nullptr) //单节点
h1->left = h2; //h1中其他的域已经精确
else {
h1->right = merge(h1->right, h2);
if (h1->left->npl < h1->right->npl)
swapChildren(h1);
h1->npl = h1->right->npl + 1;
}
return h1;
}
void swapChildren(LeftisNode* t)
{
LeftisNode* tmp = t->left;
t->left = t->right;
t->right = tmp;
}
/**
* 使树为空的内部方法
* 可能导致栈空间耗尽
*/
void reclaimMemory(LeftisNode* t)
{
if (t != nullptr) {
reclaimMemory(t->left);
reclaimMemory(t->right);
delete t;
}
}
LeftisNode* clone(LeftisNode* t)const
{
if (t == nullptr)
return nullptr;
else
return new LeftisNode{ t->element,clone(t->left),clone(t->right),t->npl};
}
};
斜堆
斜堆(skew heap)是左式堆的自调节形式。斜堆和左式堆间的关系类似于伸展树与AVL树间的关系。斜堆的右路径在任何时刻都可以任意长,因此,所有操作的最坏情形运行时间均为O(N)。
与左式堆相同,斜堆的基本操作也是合并。对于左式堆,我们查看是否左儿子和右儿子满足左式堆结构性质并在不满足该性质时将它们交换。但对于斜堆,交换是无条件的,除那些右路径上所有节点的最大值不交换它的左右儿子的例外之外,其余都需要进行这种交换。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号