软工作业3：结对项目

学生个人信息

姓名	学号
詹炜昊	3121005102
李境豪	3121005093

作业要求

这个作业属于哪个课程	软件工程
这个作业要求在哪里	作业链接
这个作业的目标	实现四则运算题目的命令行程序

GitHub

GitHub链接

PSP表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	50	60
· Estimate	· 估计这个任务需要多少时间	400	420
Development	开发	215	190
· Analysis	· 需求分析 (包括学习新技术)	100	120
· Design Spec	· 生成设计文档	25	30
· Design Review	· 设计复审	25	30
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	20	20
· Design	· 具体设计	20	25
· Coding	· 具体编码	20	30
· Code Review	· 代码复审	30	30
· Test	· 测试（自我测试，修改代码，提交修改）	50	60
Reporting	报告	30	70
· Test Repor	· 测试报告	30	40
· Size Measurement	· 计算工作量	30	20
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	40	50
	· 合计	1085	1195

需求分析

题目：实现一个自动生成小学四则运算题目的命令行程序（也可以用图像界面，具有相似功能）。
说明：
自然数：0, 1, 2, …。

真分数：1/2, 1/3, 2/3, 1/4, 1’1/2, …。
运算符：+, −, ×, ÷。
括号：(, )。
等号：=。
分隔符：空格（用于四则运算符和等号前后）。
算术表达式：
e = n | e1 + e2 | e1 − e2 | e1 × e2 | e1 ÷ e2 | (e),

其中e, e1和e2为表达式，n为自然数或真分数。

四则运算题目：e = ，其中e为算术表达式。

需求

· 使用 -n 参数控制生成题目的个数

· 使用 -r 参数控制题目中数值（自然数、真分数和真分数分母）的范围

· 生成的题目中计算过程不能产生负数

· 每道题目中出现的运算符个数不超过3个

· 去重

· 生成的题目存入执行程序的当前目录下的Exercises.txt文件

· 其中真分数在输入输出时采用如下格式，真分数五分之三表示为3/5，真分数二又八分之三表示为2’3/8

· 在生成题目的同时，计算出所有题目的答案，并存入执行程序的当前目录下的Answers.txt文件

· 程序应能支持一万道题目的生成

· 程序支持对给定的题目文件和答案文件，判定答案中的对错并进行数量统计

具体实现

效能分析

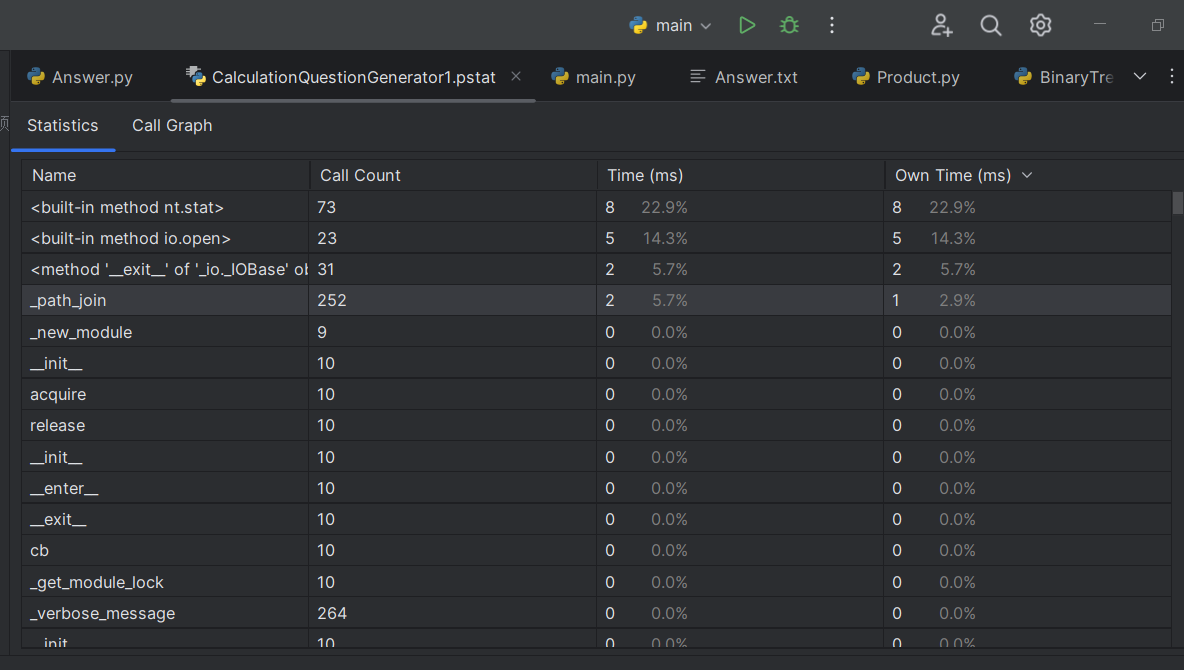
main的效能分析

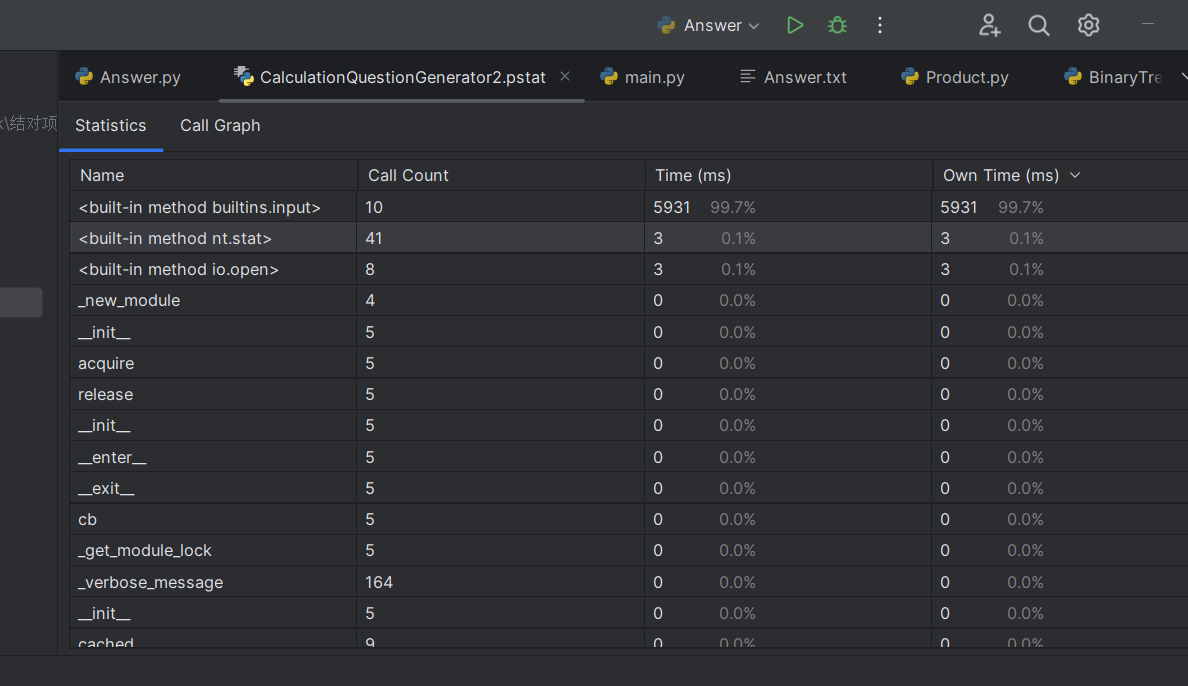
answer的效能分析

设计实现过程

共有五个类

Product：生成表达式
Answer：生成答案
main：主函数
BinaryTree：二叉树算法
SuffixExpression：将中缀表达式转化为后缀表达式，计算后缀表达式的值

代码说明

生成算式

一个算式由多个运算符和多个运算数组成，如果要生成算式，则需要确保每个运算符的左右两侧都有一个运算数。为了满足这个要求，我们可以使用二叉树结构进行描述，每个结点表示一个运算符或者一个运算数。根节点表示整个算式的最外层运算符，每个节点最多可以存在两个子节点，表示该节点对应运算符的左右两个运算数或运算子式。

因此，我们可以将根节点看作一个运算符，它的左右两个子节点可以是运算符或运算数。如果一个子节点也是一个运算符，那么我们可以在该节点上再次应用相同的操作，为它生成左右两个运算数或运算子式，并继续向下递归，直到达到预设的层数，或者所有叶子节点都是运算数。

最后，我们将多余的叶子节点填入运算数即可生成一条正确的算式。
主要用了二叉树来实现：
`class Node:

def __init__(self, value):
    self.value = value
    self.left = None
    self.right = None

class BinaryTree:

treeStack = []  #二叉树
expression = []  #表达式

def __init__(self):
    #print("创建二叉树类")
    pass


def shengcerchashu(self,exp):
    """生成"""
    self.expression  = exp
    for item in self.expression:
        #print(item)
        parent = Node(item)
        if not item in  ['+', '-', 'x', '÷']:
            #操作数
            self.treeStack.append(parent)
        else:
            #运算符
            right = self.treeStack.pop()
            left = self.treeStack.pop()
            parent.right = right
            parent.left = left
            self.treeStack.append(parent)


    #二叉树的根
    parent = self.treeStack[-1]

    return parent

def treeIsSame(self,root):
    """判断是否相同"""
    if not root.left:
        if not root.right:
            return root.value
    elif root.value == '+' or root.value == 'x':
        left = self.treeIsSame(root.left)
        right = self.treeIsSame(root.right)
        if operator.le(left, right):
            #print(root.value + left + right)
            return root.value + left + right
        else:
            return root.value + right + left
    else:
        return root.value + self.treeIsSame(root.left) + self.treeIsSame(root.right)

`

小括号的处理

遍历每个单词item，如果是运算符，则弹出ops_stack栈顶并将其加入suffix_stack栈中，直到找到插入位置为止；如果是左括号，则直接压入ops_stack中；如果是右括号，则不断弹出ops_stack栈顶并将其加入suffix_stack栈中，直到找到左括号为止；否则，就是数字，直接加入suffix_stack栈中。最后，把ops_stack栈中剩余的操作符都取出并加入suffix_stack栈中，返回suffix_stack栈，也就是后缀表达式的结果。
`
def toSuffix(self):

    if not self.zhongzhui:
        return []
    ops_rule = {
        '+': 1,
        '-': 1,
        '×': 2,
        '÷': 2,
    }
    suffix_stack = []  # 后缀表达式结果
    ops_stack = []  # 操作符栈
    infix = self.zhongzhui.split(' ')   # 将表达式分割得到单词
    # print(infix)
    for item in infix:

        if item in ['+', '-', '×', '÷']:  # 遇到运算符
            while len(ops_stack) >= 0:
                if len(ops_stack) == 0:
                    ops_stack.append(item)
                    break
                op = ops_stack.pop()
                if op == '(' or ops_rule[item] > ops_rule[op]:
                    ops_stack.append(op)
                    ops_stack.append(item)
                    break
                else:
                    suffix_stack.append(op)
        elif item == '(':  # 左括号直接入栈
            ops_stack.append(item)
        elif item == ')':  # 右括号
            while len(ops_stack) > 0:
                op = ops_stack.pop()
                if op == "(":        # 一直搜索到出现“(”为止
                    break
                else:
                    suffix_stack.append(op)
        else:
            suffix_stack.append(item)  # 数值直接入栈

    while len(ops_stack) > 0:
        suffix_stack.append(ops_stack.pop())

    self.re =suffix_stack
    return suffix_stack

`

计算答案

读取表达式列表中的每个表达式，计算其结果，并将结果以"AnswerX: Y"的格式写入文件"Answer.txt"中，其中X表示表达式的序号，Y表示表达式的计算结果。
`class Answer:

exp_list = []
exercisefile  = ""
answerfile  = ""

def __init__(self):
    print("Answer")

def expression_result(self,exp_list):
    """
    求表达式的结果
    """

    self.exp_list  =exp_list
    if os.path.exists('Answer.txt'):   # 清空上一次的答案
        with open('Answer.txt', 'r+') as file:
            file.truncate(0)

    for i, exp in enumerate(self.exp_list):
        order_str = str(i + 1)
        suffixExpression  = SuffixExpression(exp)
        #print("------suffixExpression:{}---------".format(str(suffixExpression.suffixToValue()) ))
        exp_value = str(suffixExpression.suffixToValue()) + '\n'
        result = "Answer"+order_str + ': ' + exp_value

        with open('Answer.txt', 'a+', encoding='utf-8') as f:
            f.write(result)`

测试运行

生成题目如下

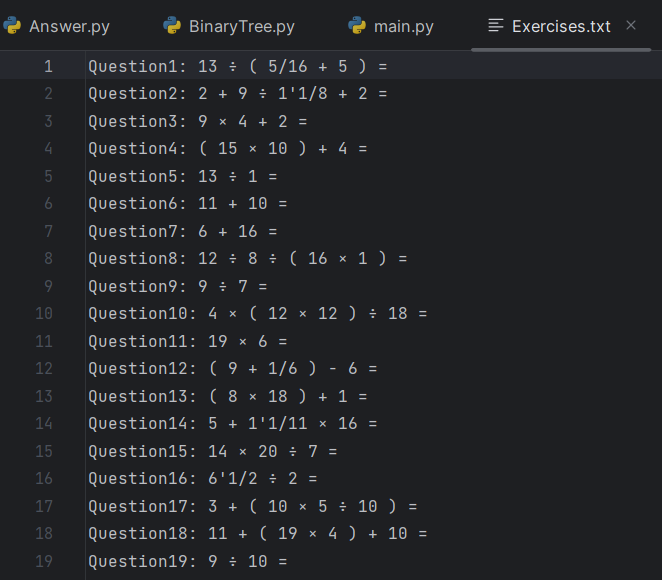
生成答案

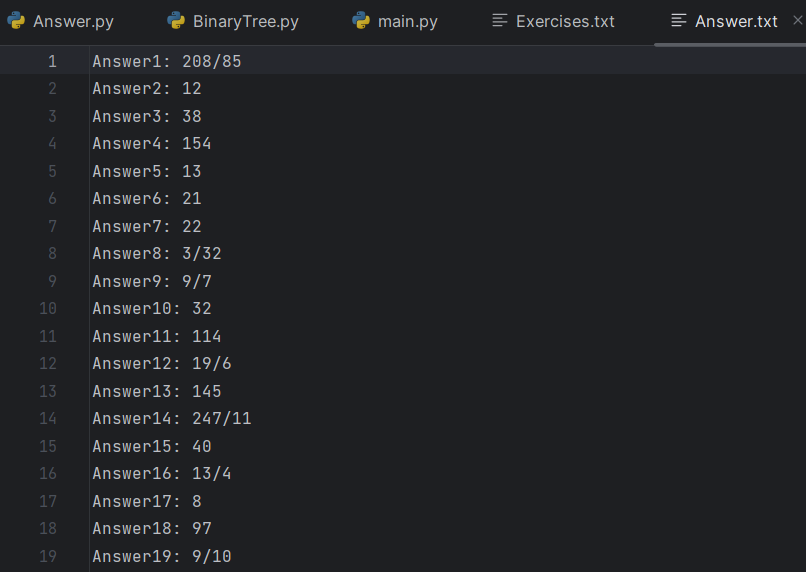
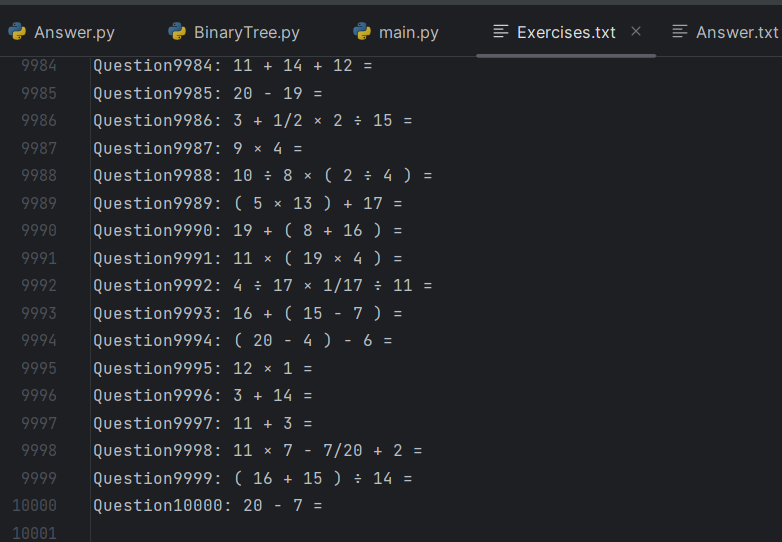
支持生成一万条题目，如下图

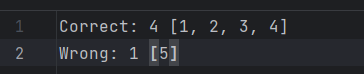
对于生成4条题目，用户输入答案以及计算机判断正误的运行结果如下

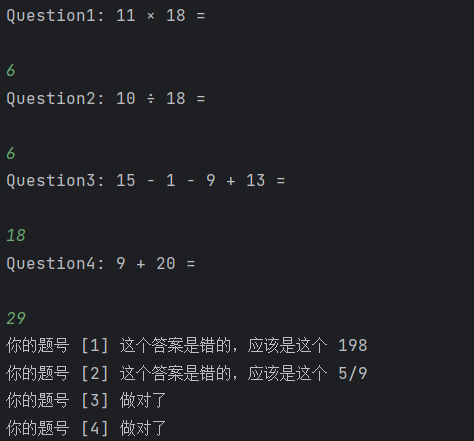
得分如下

五条题目也同理，经过计算均符合要求

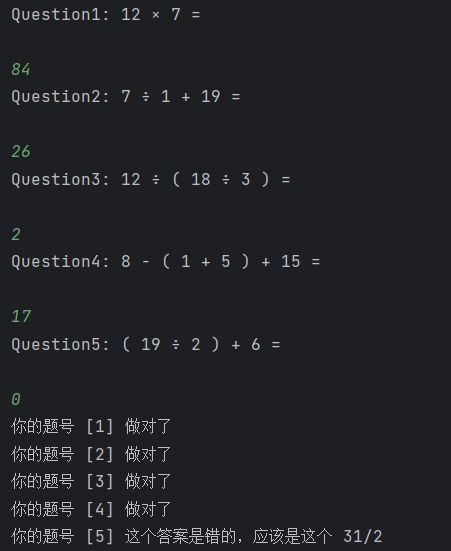
项目小结

在这个结对项目中，我另一位成员紧密合作，共同完成了这一个四则运算任务。通过结对编程的方式，我们成功地实现了项目的目标。
我觉得这次项目提高了两个人之间的协作能力。通过和另一个人一起工作，我们可以学会如何交流，如何协调，如何共同解决问题。在这个过程中，我们被迫更加关注自己代码的清晰度和可读性，以便对方可以轻松理解我们的代码。
对于一些思想上的纠纷，我们通过了合理的沟通来解决，并且一致决定用python来实现编写，分工明确可以使我们做起项目来更加高效，对于一些算法的调试，也不是一帆风顺的，这个时候就要调整好情绪，和队友好好沟通，换一种思路继续下去，相互支持和鼓励，这也是结对项目给我们带来的一种收获吧