第五章 特征值,特征向量,对角化
- 为什么要相似对角化
-
为了将普通矩阵的n次幂转化成对角矩阵的n次幂

-
为了求解P矩阵和对焦矩阵,需要引入特征值和特征向量
- 特征值与特征向量
- 当且仅当无关的特征向量的个数 = 矩阵的阶数时,才可以相似对角化
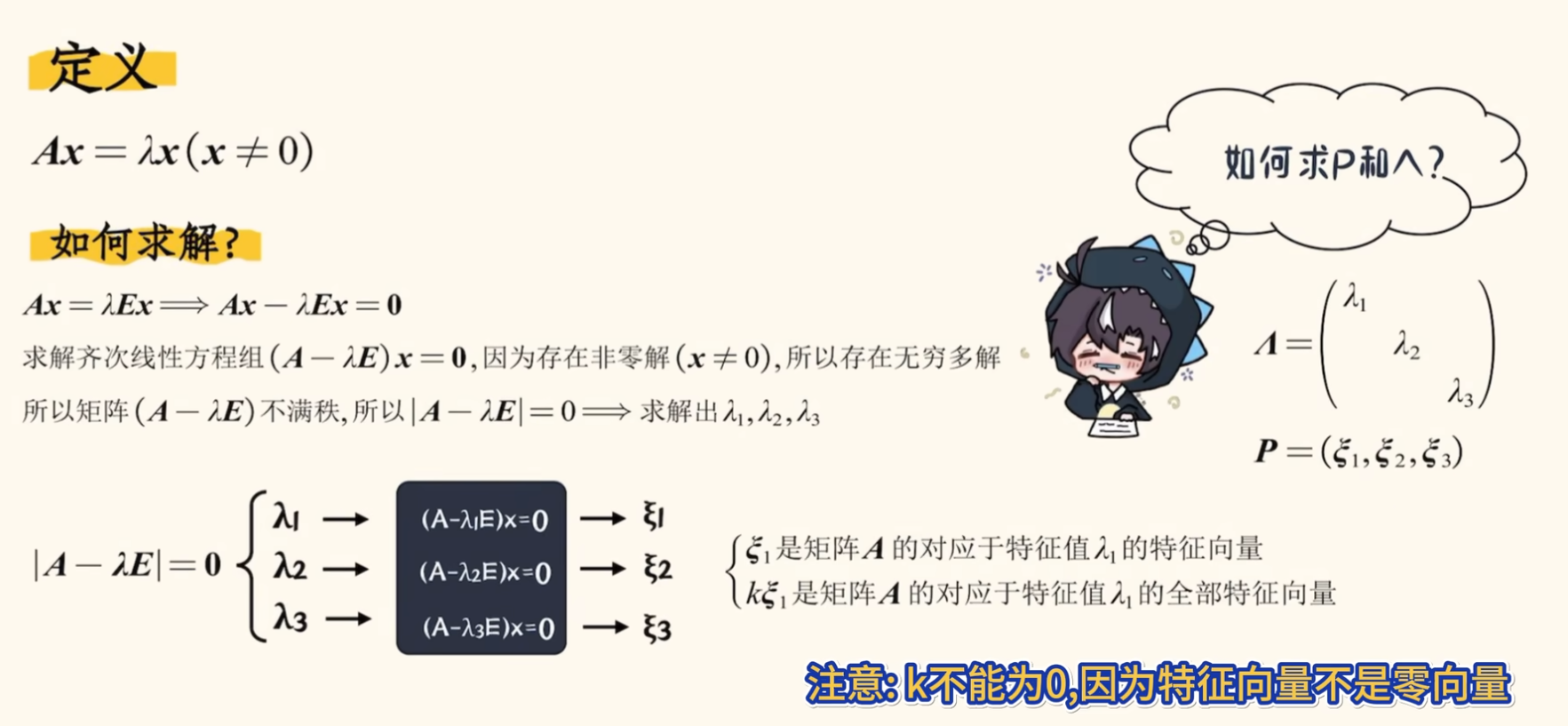

-
相似的推论

-
相似定义

-
相似对角化
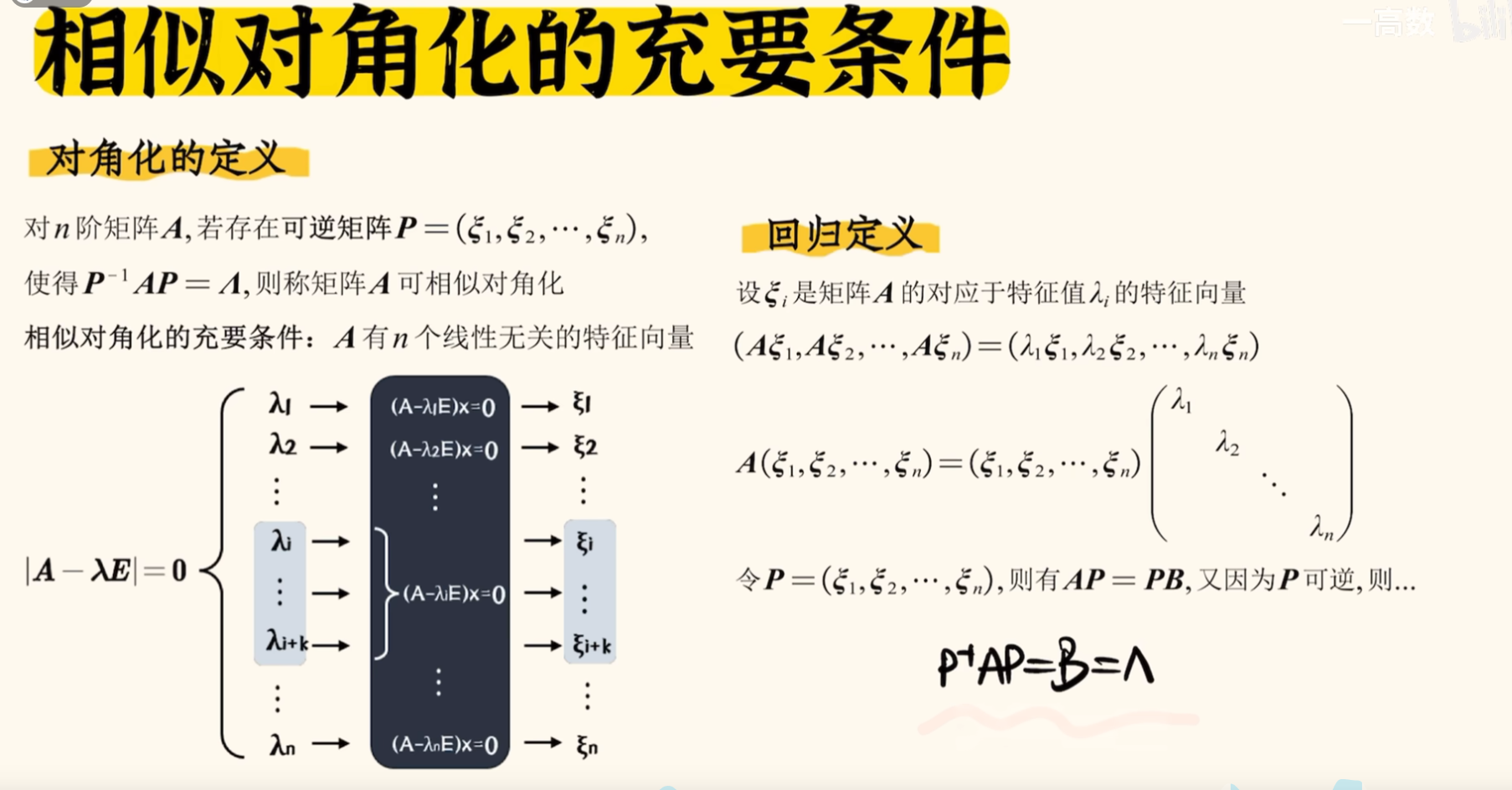
-
正交


-
对称矩阵的对角化
对称矩阵一定可以对角化,所以对于重根进行正交化求得目标矩阵,正交矩阵必须是单位化的
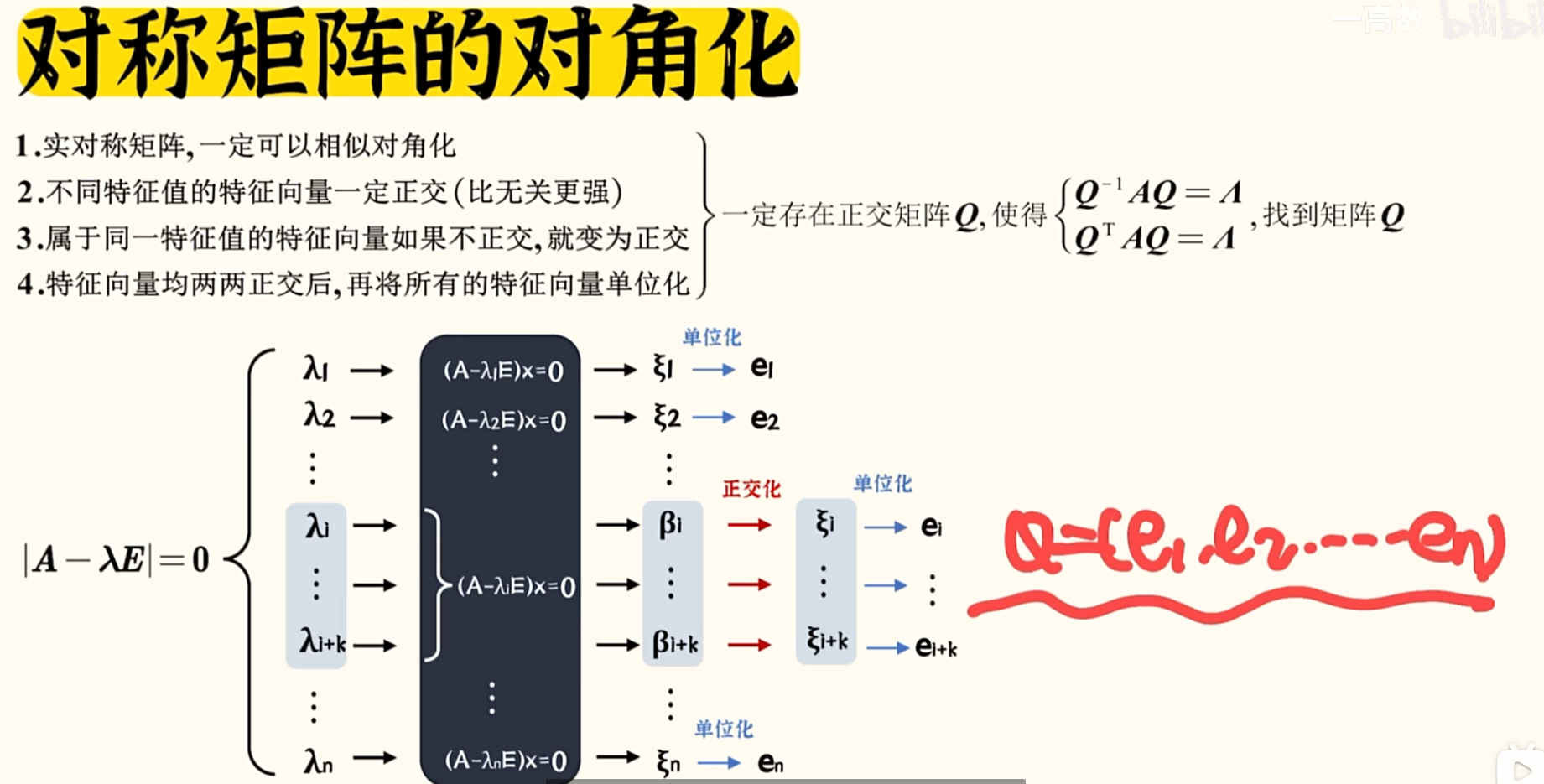
为了将普通矩阵的n次幂转化成对角矩阵的n次幂

为了求解P矩阵和对焦矩阵,需要引入特征值和特征向量


相似的推论

相似定义

相似对角化

正交


对称矩阵的对角化
对称矩阵一定可以对角化,所以对于重根进行正交化求得目标矩阵,正交矩阵必须是单位化的

