计算机视觉之滤波器大法
1. 滤波器定义
滤波器名字顾名思义,就是能够把原始数据过滤掉一部分的一种机器。
滤波本质上是一种特殊的函数,其作用在图像的每个位置,通过定义的计算方式得到输出,输出的值用于替换图像当前位置(滤波器中心)的值。
令滤波函数为
g(x;w),其中x为图像的局部邻域,w为滤波器的权重,滤波器可以分成如下3类,
线性滤波器(Linear filter):线性滤波的输出为输入的线性组合,即
g=w⋅x,线性滤波器最为常见;
非线性滤波器(Non-Linear Filter):不满足上条性质的为非线性滤波,典型的非线性滤波如最大值/最小值/中值滤波、膨胀/腐蚀等;
自适应滤波器(Adaptive filter):线性滤波中的w在滑动过程中固定不变(与图像内容独立无关),自适应滤波的w在滑动过程中会随着窗口内像素的性质和结构发生变化。直觉上,自适应滤波器在某些复杂情况下可能取得更好的效果,但相对线性滤波器,其计算代价更高也更难优化加速。
图像滤波是一种比较常用的方法,通过滤波操作,就可以突出一些特征或者去除图像中不需要的成分。通过选取不同的滤波器,在原始图像上进行滑动和卷积,借助相邻的像素值就可以决定该像素最后的输出。最常见的算子分为两类,一个是图像平滑去噪功能、一个是边缘检测功能,下文中会对这两类进行展开。
2. 滤波器分类
2.1 平滑滤波器
均值滤波、中值滤波、高斯滤波的基本原理都是以一个滑动窗口,以指定的计算方式得到其中的值,将它输出到信号的当前位置,
2.1.1 高斯滤波
高斯滤波器是一种可以使图像平滑的滤波器,用于去除噪声。
高斯滤波器将中心像素周围的像素按照高斯分布加权平均进行平滑化。这样的二维权值通常被称为卷积核(kernel)或者滤波器(filter)。
但是,由于图像的长宽可能不是滤波器大小的整数倍,同时我们希望输出图像的维度与输入图像一致,因此我们需要在图像的边缘补0,具体补几个0视滤波器与图像的大小关系确定,这种方法称作Zero Padding。同时,权值g(卷积核)要进行归一化操作(∑ g = 1)。
高斯滤波在减少噪声的同时,能够较好地保留图像的边缘信息。
按下面的高斯分布公式计算权值:
2.1.2 中值滤波
中值滤波器也是一种可以使图像平滑的滤波器,一定程度上可以去除图像的噪声,同时图像的细节也会变得模糊。这种滤波器是提取出滤波器范围内(在这里假设是3 × 3)像素点的中值。为了保证输出图像的大小和输入一样,需要采用Zero Padding。
2.1.3 均值滤波
与中值滤波相似,均值滤波也是用于图像降噪的。唯一与中值滤波不同的是,均值滤波对于滤波器范围内的像素点,计算他们的均值作为输出。
这种滤波器对于减少图像中的随机噪声非常有效。
import cv2
import numpy as np
# 读取图像
image = cv2.imread('1.jpg', cv2.IMREAD_GRAYSCALE)
# 定义均值滤波器
kernel_size = 5
mean_filter = np.ones((kernel_size, kernel_size), np.float32) / (kernel_size * kernel_size)
# 应用均值滤波
smoothed_image = cv2.filter2D(image, -1, mean_filter)
# 显示结果
cv2.imshow('Mean Filtered Image', smoothed_image)
cv2.waitKey(0)
cv2.destroyAllWindows()
# 使用高斯滤波
smoothed_image = cv2.GaussianBlur(image, (kernel_size, kernel_size), 0)
# 显示结果
cv2.imshow('Gaussian Filtered Image', smoothed_image)
cv2.waitKey(0)
cv2.destroyAllWindows()
# 使用中值滤波
blurred_image = cv2.medianBlur(image, kernel_size)
cv2.imshow('median Filtered Image', smoothed_image)
cv2.waitKey(0)
cv2.destroyAllWindows()



2.2 边缘检测滤波器
边缘检测用于检测图像中的线。通常这样提取图像中的信息的操作被称为特征提取。
边缘检测通常在灰度图像上进行。
2.2.1 Sobel滤波器
Sobel算子可以近似的计算出图像相邻像素之间的梯度。假设滤波器现在滑动到背景部分,那么滤波器卷积计算得到的值就非常小;反之,如果滤波器在背景和前景分界出,那么滤波器滑过得到的卷积数值就会比较大。因此可以较好的提取出图像的边缘信息。
# python
# 边缘检测 Sober索贝尔算子
# 对噪声具有平滑作用,提供较为精确的边缘方向信息,边缘定位精度不够高。
# @Zivid 2021/8/16
import cv2
import numpy as np
from skimage import filters
# 方法一 自定义
def def_sober(gray_img):
# 算子
x_sobel = np.array([[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]])
y_sobel = np.array([[-1, -2, -1],
[0, 0, 0],
[1, 2, 1]])
h, w = gray_img.shape
img = np.zeros([h + 2, w + 2], np.uint8)
img[2:h + 2, 2:w + 2] = gray_img[0:h, 0:w]
x_edge_img = cv2.filter2D(img, -1, x_sobel)
y_edge_img = cv2.filter2D(img, -1, y_sobel)
edge_img = np.zeros([h, w])
for i in range(h):
for j in range(w):
edge_img[i][j] = np.sqrt(x_edge_img[i][j] ** 2 + y_edge_img[i][j] ** 2) / (np.sqrt(2))
return edge_img
# 方法二 系统自带opencv
def cv2_sober(img):
# 算子
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # 灰度化
sobel_x = cv2.Sobel(gray, cv2.CV_8U, 1, 0) # 通过控制dx,dy的值来控制梯度的方向,这里是求x方向的梯度
sobel_y = cv2.Sobel(gray, cv2.CV_8U, 0, 1) # 这里是求y方向的梯度
sobel = cv2.Sobel(gray, cv2.CV_8U, 1, 1) # 这里是求x,y方向综合的梯度
return [sobel_x, sobel_y, sobel]
# 方法三 直接调用系统自带 skimage库内的函数
def skimage_sobel(img):
edge_pic = filters.sobel(img)
return edge_pic
if __name__ == '__main__':
# 读取图像
img = cv2.imread('1.jpg', cv2.COLOR_BGR2GRAY)
rgb_img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) # 先转化成RGB
# 灰度化处理图像
grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
cv2.imshow('original', grayImage)
pic1 = def_sober(grayImage)
cv2.imshow('def_sober', pic1)
pic2 = skimage_sobel(grayImage)
cv2.imshow('skimage_sobel', pic2)
sobel_x,sobel_y,sobel = cv2_sober(img)
cv2.imshow("cv2_Sobel_x", sobel_x)
cv2.imshow("cv2_Sobel_y", sobel_y)
cv2.imshow("cv2_Sobel", sobel)
cv2.waitKey(0)
2.2.2 Prewitt滤波器
Prewitt算子与Sobel算子不同的是,Sobel算子考虑了权值的因素,即在中心点正上方或正下方(正左和正右)的权值为2,因为这个像素点离中心更近,而离中心远一点的斜侧方的权值为1;而Prewitt中没有这种设定。总的来说,Sobel算是对Prewitt的一种改进,效果也自然更好一点。
# python
# 边缘检测 Prewitt普利维特算子
# 利用像素点上下、左右邻点灰度差,在边缘处达到极值检测边缘。对噪声具有平滑作用
# @Zivid 2021/8/16
import cv2
import numpy as np
from skimage import filters
# 方法一 自定义
# python
# 边缘检测 Prewitt普利维特算子
# 利用像素点上下、左右邻点灰度差,在边缘处达到极值检测边缘。对噪声具有平滑作用
# @Zivid 2021/8/16
import cv2
import numpy as np
from skimage import filters
# 方法一 自定义
def prewitt01(pic):
# 算子
x_kernel = np.array([[1, 1, 1], [0, 0, 0], [-1, -1, -1]], dtype=int)
y_kernel = np.array([[-1, 0, 1], [-1, 0, 1], [-1, 0, 1]], dtype=int)
x = cv2.filter2D(pic, cv2.CV_16S, x_kernel)
y = cv2.filter2D(pic, cv2.CV_16S, y_kernel)
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)
Prewitt1 = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)
return Prewitt1
# 方法二 直接调用系统自带 skimage库内的函数
def sys_prewitt(pic):
edge_img = filters.prewitt(pic)
return edge_img
if __name__ == '__main__':
# 读取图像
img = cv2.imread('1.jpg', cv2.COLOR_BGR2GRAY)
rgb_img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) # 先转化成RGB
# 灰度化处理图像
grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
cv2.imshow('original', grayImage)
pic1 = prewitt01(grayImage)
cv2.imshow('Prewitt01', pic1)
pic2 = sys_prewitt(grayImage)
cv2.imshow('Prewitt02', pic2)
cv2.waitKey(0)
2.2.3 Laplacian滤波器
有别于Sobel算子和Prewitt算子这两类一阶微分滤波器,Laplacian滤波器是对图像亮度进行二次微分从而检测边缘的滤波器。由于数字图像是离散的,x方向和y方向的一次微分分别按照以下式子计算:
对于 ( I_x(x, y) ):
对于 ( I_y(x, y) ):
所以二次微分按照以下式子计算:
对于 ( I_{xx}(x, y) ):
将 ( I_x(x, y) ) 展开,得到:
最后的结果是:
同理:
对于 ( I_{yy}(x, y) ):
因此,Laplacian 表达式为:
展开为:
把这个式子表示为卷积核是下面这样的:
import cv2
img = cv2.imread("1.jpg", cv2.IMREAD_UNCHANGED)
laplacian=cv2.Laplacian(img,cv2.CV_64F,ksize=1)
result=cv2.convertScaleAbs(laplacian)
cv2.imshow("img", img)
cv2.imshow("result", result)
cv2.waitKey()
cv2.destroyAllWindows()
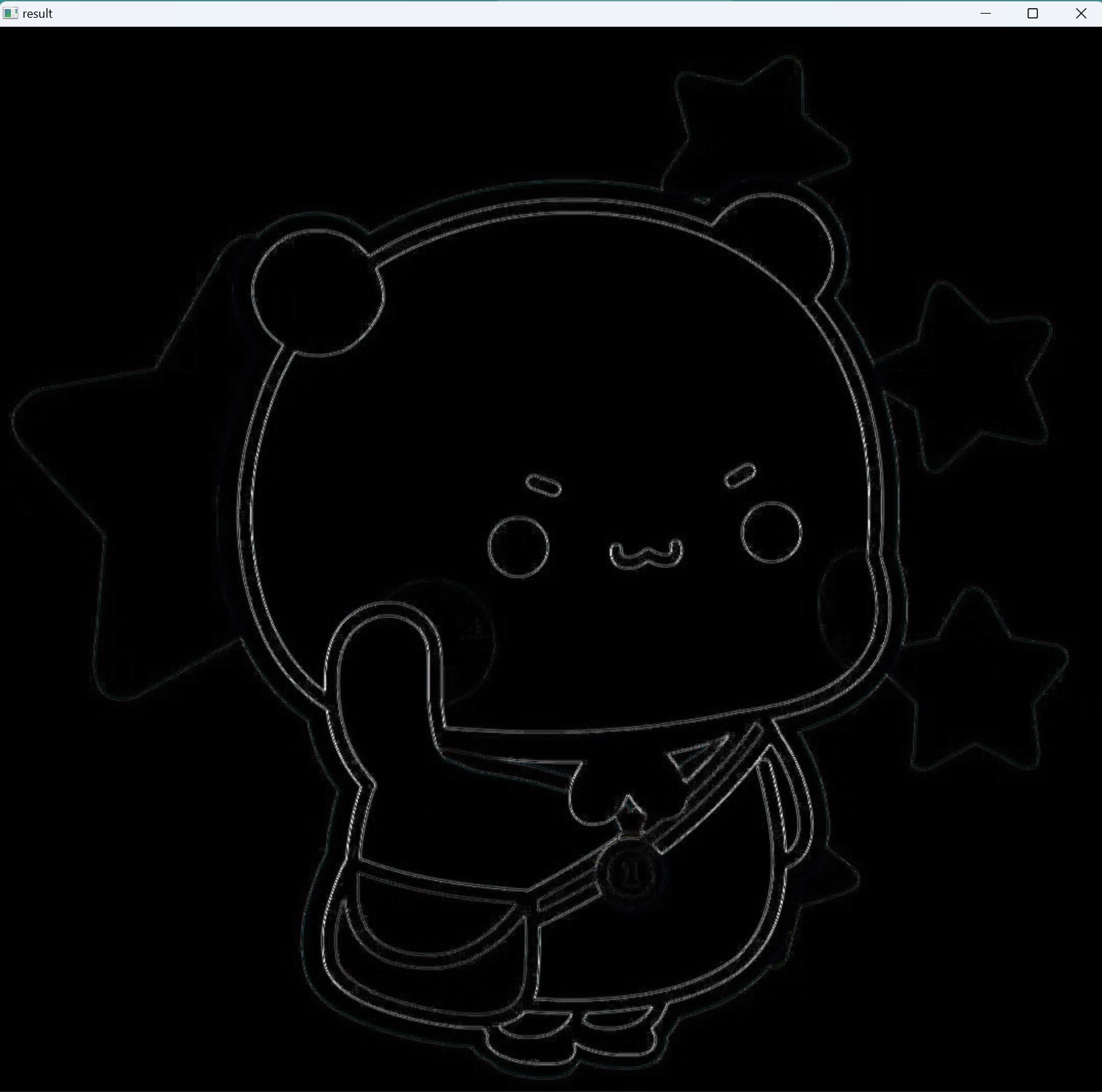
2.2.4 MAX-MIN滤波器
MAX-MIN滤波器是一种常见的边缘检测滤波器,其使用网格内像素的最大值和最小值的差值对网格内像素重新赋值。
3. Padding(填充)
滤波操作不可避免的一个问题是边界如何处理,当滤波器的中心压在图像边界处时,滤波器会有一部分落在图像外,但图像外并没有像素,该如何处理?通常需要对图像进行填充(padding),填充需要解决2个问题,填充的元素取什么值以及填充多少个元素。
对于延拓元素的取值,通常有4种方式,
- 常数填充(0填充):填充的元素取相同的常数值
- 周期填充(circular):认为图像的上下左右被与自身相同的图像包围着
- 复制填充(replicate):复制图像边界的元素
- 对称填充(symmetric):填充的元素与图像关于边界对称
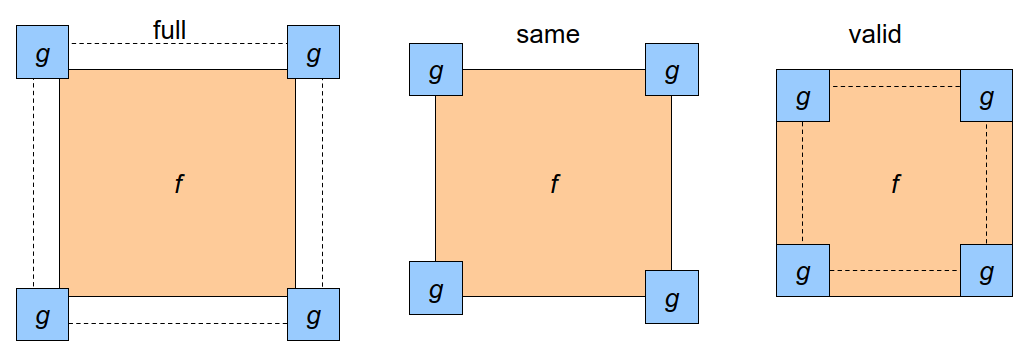
对于填充多少个元素,通常有3种方式,令滤波器的大小为g×g,图像大小为f×f,
full:边界分别填充g−1个元素,滤波结果为(f+g−1)×(f+g−1),比原图大
same:边界分别填充(g−1)/2个元素,滤波结果为f×f,与原图大小相同
valid:边界不填充,滤波结果为(f−g+1)×(f−g+1),比原图小
友链:
图像处理 | 最常用的边缘检测详解与代码(Robert, Sober, Prewitt, Canny, Kirsch, Laplacian, LOG, DOG算子)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号