线段树详解
授人以鱼不如授人以渔
本文尽量详细地讲述线段树的引入,实现,应用,以及相关进阶知识。
引入
引入线段树通用的例子:
给定一组整数\(nums\),定义两种操作
-
修改列表里的第\(i\)个数据为\(val\) ①
-
查询区间和\([L,R]\) ②
为了同时实现两种操作,现在考虑处理\(nums\)的方式
简单的,可以直接使用数组。
此时对于操作①,简单赋值nums[i] = v即可。复杂度\(O(1)\)。但是此时想执行
操作②,却需要枚举计算\(\sum_{i=L}^Rnums[i]\),这个复杂度是\(O(n)\)的。
稍微进阶一点,可以使用前缀和数组。
此处面向小白单独再解释下前缀和。
已知数组\(a\),定义前缀和数组\(pre[n+1]\),\(pre[i]\)表示数组\(a\)的前\(i\)项之和,即\(pre[i]=\sum^{i-1}_{j=0}a[j]\),特别的\(pre[0]\)表示不选择任何前缀,\(pre[0]=0\)。
重要引申:\(a\)的子数组\([L,R]\)内的元素和,即\(a[L]+\cdots+a[R] =\sum_{i=L}^{R}a[i]=pre[R+1]-pre[L]\)
所以预处理原数据,生成前缀和数组,此时对于操作②,\(\sum_{i=L}^Rnums[i]=pre[R+1]-pre[L]\)是可以以\(O(1)\)计算的。
但是此时对于操作①,修改任意\(nums[i]\)都需要对\(pre[i+1]\sim pre[n]\)的所有前缀和修改,反而是\(O(n)\)的。
综合来看,两种处理策略都是一种操作\(O(1)\),另一种操作\(O(n)\),混合操作显然复杂度均为\(O(n)\)
如何可以同时处理两种操作且单次复杂度均低于\(O(n)\)?
线段树应运而生。Jon Bentley 1977年在解决Klee提出的问题 时发明出线段树
对于上述两种操作,线段树均能以单次\(O(logn)\)复杂度完成。
线段树代码复杂,应用广泛,还有各种变种和进阶知识。是小白到进阶的分水岭。
基本实现
线段树,顾名思义,树的节点上存储的是一个区间数据(线段)
下面用数组构造一颗最基础的线段树。
根节点表示的是整个\([0\sim n-1]\)范围数据之和
假设root是根节点,有\(root.sum = \sum_{i = 0}^{n-1}nums[i]\)。
对于每个节点,其左右子节点分别代表当前节点左右两半区间的数据,然后递归建立这棵树。
前n个叶节点对应数组\(nums\)。
线段树可看做是一颗完全二叉树。
从数学角度可以计算线段树中至多有多少个节点:
数组\(nums\)长度为\(n\),如果\(n\)为2的幂,则可以构成一颗完全二叉树,此时节点数为\(2n-1\)。
\(n\)可能不为2的幂时,考虑极限情况取\(n=2^k+1\),此时这颗完全二叉树会多出一层,这层个数为\(2*(n-1)\),整体为\(4n-5\)。
一般的,通常初始化数组长度为\(4n\)。
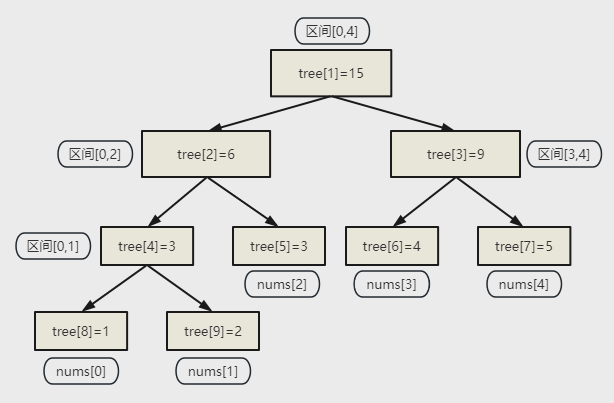
以数组\([1,2,3,4,5]\)为例,线段树节点数组定义为vector<int> tree
以数组方式存树时,习惯节点下标从1开始,若当前节点位置为\(p\),则左右孩子节点可以简单表示为\(p*2\),\(p*2+1\)
本例中,根节点\(tree[1]=15\),表示原数组区间\([0,4]\)和为15。
以下递归进行:
每次对当前节点区间折半处理,左半部分是左子树数据,右半部分是右子树数据
则有\(tree[2]=6\),代表区间\([0,2]\)和为15。\(tree[3]=9\),代表区间\([3,4]\)和为9。
\(\cdots\)
下面基于这颗树,来处理这两种操作。
首先写一个简单的模板定义,结构如下:
class SegmentTree
{
public:
SegmentTree(int n) { this->n = n; tree.resize(n * 4); }; //4n定义
void Update(int i, int val) { ... } //操作1
int Sum(int l, int r) { return ... } //操作2
private:
int n; //原始数据的长度
vector<int> tree; //树结构数组
}
单点修改
通常称操作1为单点修改
显然,当我们修改某一项时,必须要对应修改包含了该点的所有区间节点。
比如修改\(nums[2]=0\),则节点1(表示区间[0-4]),节点2(表示区间[0-2]),节点5(表示区间[2-2]),均需要同步修改。
具体地,我们要做的是:
-
自顶向下递归地分割区间,直到定位到目标节点
-
自底向上合并结果,从目标节点的修改,向上逐步修改父节点的结果。
以下是基础版线段树单点修改代码
//API,更新原数据第i个位置为val i∈[0,n-1]
void Update(int i, int val) { Update(1, 0, n - 1, i, val); }
//具体实现
void Update(int p, int s, int t, int i, int val)
{
if (s == t)
{
tree[p] = val;
return;
}
//分治
int mid = (s + t) >> 1;
if (i <= mid) Update(p * 2, s, mid, i, val);
if (i > mid) Update(p * 2 + 1, mid + 1, t, i, val);
//合并
tree[p] = tree[p * 2] + tree[p * 2 + 1];
}
单次修改复杂度是\(O(logn)\)
以上是一段优美简洁的分治思想代码,建议细品。
p表示的是当前节点索引,对应tree数组中,p的范围大致是[1,4n]
[s,t]表示的就是p节点管辖的区间
目标是定位到原数组中位置i最终所占的区间[i,i],递归函数的出口处有s=t=i
区间查询
通常称操作2为区间查询
容易理解的是,1号根节点表示区间[0,n-1]也就是所有元素和。
向下,2号节点是左半区间,3号节点是右半区间。
递归向下,依次可以得到不同的区间数据。
但是这些区间都是"折半区间",当待查区间是任意区间时,比如查询[0,3]?
类似单点查询,同样需要递归分治处理。
以数组范围[0,n-1],目标区间[l,r]为例
当递归处理到某个节点区间[s,t]时,如果这个区间被目标区间完全覆盖,则可以直接返回该节点的区间和。
否则,将当前区间折半,如果左侧或者右侧的区间与目标区间有交集,则递归进入计算,否则可以忽略。
最终返回左右区间结果的和。
具体代码如下:
//API 查询原数组[l,r]区间和 l,r∈[0,n -1]
int Sum(int l, int r) { return Sum(1, 0, n - 1, l, r); }
//具体实现
int Sum(int p, int s, int t, int l, int r)
{
if (s >= l && t <= r) return tree[p];
int res = 0;
int mid = (s + t) >> 1;
if (l <= mid) res += Sum(p * 2, s, mid, l, r);
if (r > mid) res += Sum(p * 2 + 1, mid + 1, t, l, r);
return res;
}
至此,我们实际完成了基础线段树的核心部分,同时可以处理操作12,且单次操作复杂度均为\(O(logn)\)
模板题,LeetCode上307. 区域和检索 - 数组可修改
class NumArray {
public:
SegmentTree* tree;
NumArray(vector<int>& nums) {
int n = nums.size();
tree = new SegmentTree(n);
for (int i = 0; i < n; i++) tree->Update(i, nums[i]);
}
void update(int index, int val) {
tree->Update(index, val);
}
int sumRange(int left, int right) {
return tree->Sum(left, right);
}
};
建树
注意上述代码里,初始化树的过程中,我们枚举了每个原数组下标,调用了:
for (int i = 0; i < n; i++) tree->Update(i, nums[i]);
显然这个复杂度为\(O(nlogn)\)。虽然也能通过本题,但是在标准线段树处理里,可以通过一次递归,完成所有数据的初始化
由于只有\(4n\)个节点,因此建树的复杂度可以降为\(O(n)\)。
更具体地,本题中设数组长度为\(n\),查询次数为\(m\),
则整体复杂度可以从\(O(nlogn+mlogn)\)降为\(O(n+mlogn)\)。
这是一个常数优化,标准线段树中一般会包含建树处理。
void Build(vector<int>& nums) { Build(1, 0, n - 1, nums); }
void Build(int p, int s, int t, vector<int>& nums)
{
if (s == t)
{
tree[p] = nums[s];
return;
}
int mid = (s + t) >> 1;
Build(p * 2, s, mid, nums);
Build(p * 2 + 1, mid + 1, t, nums);
tree[p] = tree[p * 2] + tree[p * 2 + 1];
}
这样原数组的初始化可以改为简单调用 tree->Build(nums);
合并操作
注意到刷新区间和时的代码,在建树和单点修改都写了
tree[p] = tree[p * 2] + tree[p * 2 + 1];
本质是依据左右子节点数据合并到当前节点数据
本例子可能只有一句,但是线段树在复杂应用中会有较多修改。
一般来说放到一个统一的函数内处理较为合理。
一般命名为PushUp 或者Merge 之类。
void PushUp(int p)
{
tree[p] = tree[p * 2] + tree[p * 2 + 1];
//如果是复杂应用 可能还会有别的处理
}
是不是也有PushDown?是的,后面会用到
最后借用这个模板题307. 区域和检索 - 数组可修改 贴一下完整代码
基础版线段树
支持单点修改,查询区间和。
//基础线段树模板
class SegmentTree {
public:
SegmentTree(int n) { this->n = n; tree.resize(n * 4); }
//建树
void Build(vector<int> nums) { Build(1, 0, n - 1, nums); }
//单点修改
void Update(int i, int val) { Update(1, 0, n - 1, i, val); }
//区间查询
int Sum(int l, int r) { return Sum(1, 0, n - 1, l, r); }
private:
int n;
vector<int> tree;
void Build(int p, int s, int t, vector<int>& nums) {
if (s == t)
{
tree[p] = nums[s];
return;
}
int mid = (s + t) >> 1;
Build(p * 2, s, mid, nums);
Build(p * 2 + 1, mid + 1, t, nums);
PushUp(p);
}
void Update(int p, int s, int t, int i, int val) {
if (s == t)
{
tree[p] = val;
return;
}
int mid = (s + t) >> 1;
if (i <= mid) Update(p * 2, s, mid, i, val);
if (i > mid) Update(p * 2 + 1, mid + 1, t, i, val);
PushUp(p);
}
void PushUp(int p)
{
tree[p] = tree[p * 2] + tree[p * 2 + 1];
}
int Sum(int p, int s, int t, int l, int r)
{
if (s >= l && t <= r) return tree[p];
int res = 0;
int mid = (s + t) >> 1;
if (l <= mid) res += Sum(p * 2, s, mid, l, r);
if (r > mid) res += Sum(p * 2 + 1, mid + 1, t, l, r);
return res;
}
};
//模板结束
class NumArray {
public:
SegmentTree* tree;
NumArray(vector<int>& nums) {
int n = nums.size();
tree = new SegmentTree(n);
tree->Build(nums);
}
void update(int index, int val) {
tree->Update(index, val);
}
int sumRange(int left, int right) {
return tree->Sum(left, right);
}
};
树状数组和ST表
额外介绍两个类似的数据结构。
ST表: 仅支持区间查询,不支持修改。以复杂度\(O(nlogn)\)预处理,每次查询\(O(1)\)。
树状数组:同样支持单点修改和区间查询操作。而且代码实现简单,且执行效率更高(常数低),主要原因是避免了递归调用。
既然树状数组各方面都比线段树更优,那么线段树的意义是什么?
因为线段树可以支持区间修改!
更强大的线段树
区间修改
难以置信,居然可以以单次复杂度\(O(logn)\)进行区间修改。
区间修改,同样以最初的例子说明
即一次操作中选择任意区间[l,r],把该区间的元素都改为val。
如果我们用最简单的思维方式,枚举区间每个元素,单点修改为val
当区间足够宽时,这个复杂度显然是\(O(nlogn)\)的,无法接受。
模仿上面分治+合并的方式可以实现这样一种思路:
当递归到的区间[s,t]被[l,r]完全覆盖时,不需要再向下递归。
[s,t]的区间和也简明就是\(val * (t - s + 1)\)
然后向上更新区间和
此时的单次操作复杂度\(O(logn)\)
这个做法是否正确呢?有问题。
当某个区间执行过区间修改后后,再次查询区间内的某个子区间和时,得到的依然是旧值。
因为我们上面为了保证复杂度,递归到某个完全覆盖区间后会直接返回。
那么当查询这个区间的子区间时,这个子区间不知道父区间发生过修改,也无法获得最新的val。
这时,我们引入了延迟标记 (或称为懒标记)
当区间更新递归到某个区间被目标区间完整覆盖,由于复杂度问题,我们需要直接返回。
但是我们额外记录下这个区间的最新目标修改值,称为延迟标记。
如果某次区间查询(区间修改也需要)查到了这个区间的子区间,这时我们在递归中把这个标记下推到子区间。然后清空标记。
由于直到某个子区间被查询或者修改时才会触发这个标记更新,所以称为延迟标记。
标记下推的过程 一般封装为上文提到过的PushDown函数
延迟标记保证了区间修改的复杂度\(O(logn)\),同时保证了数据的正确性。
通过延迟处理降低复杂度在别的地方也有应用,比如懒删除堆等。
ps. 单点修改可看做\(L=R\)的区间修改。
具体实现上,我们额外在节点存储一个数据vector<int> data,\(data[i]\)表示该节点代表的区间被修改时的目标值,以及一个是否有未同步数据的标记vector<bool> tag
比如区间修改\([0,2]\)为2,则有\(tree[2]=2*3=6\),然后标记\(val[2]=2\) 表示节点2最新修改值为2,且\(tag[2]=true\) 表示尚未向下同步
然后当向节点2子节点访问时,先向下同步节点2的\(tag\)值,然后再调用递归逻辑,之后清除节点2的\(tag\)标记。
由于本例子是修改元素值+查询区间和,理论上可以用data是否等于零判断是否有标记。考虑到扩展性,保留了tag标记
//区间更新[l,r]为val
void Update(int p, int s, int t, int l, int r, int val)
{
if(s >= l && t <= r)
{
//直接返回,但是记录标记
tree[p] = val * (r - l + 1);
data[p] = val;
tag[p] = true;
return;
}
int mid = (s + t) >> 1;
//此处下推标记
PushDown(p, mid - s + 1, t - mid);
//...
}
//区间查询 只增加下推标记处理
int Sum(int p, int s, int t, int l, int r)
{
//...
int mid = (s + t) >> 1;
//此处下推标记
PushDown(p, mid - s + 1, t - mid);
//...
}
//下推标记函数
void PushDown(int p, int cl, int cr)
{
if (!tag[p]) return;
//标记下推到子节点
tag[p * 2] = tag[p * 2 + 1] = true;
data[p * 2] = data[p * 2 + 1] = data[p];
tree[p * 2] = data[p] * cl;
tree[p * 2 + 1] = data[p] * cr;
//清空父节点标记
tag[p] = false;
data[p] = 0;
}
节点封装
实现区间修改后,我们发现节点数据增加了不少,之前只有tree数组,又增加了两个标记数组。
如果是复杂应用可能会更多。
工程上为了可读性,一般会把节点封装到一起。比如:
class Node {
public:
long sum = 0;
bool tag = false;
long val = 0;
};
这样可以在线段树中只定义一个数组vector<Node> tree
由于单点修改等价于l=r的区间修改,所以我们直接给出一个完整的区间修改线段树。
完整模板
支持区间修改的线段树模板
注意是修改区间为目标值,以及查询区间和
class Node {
public:
long sum = 0;
bool tag = false;
long val = 0;
};
class SegmentTree {
public:
SegmentTree(int n) { this->n = n; tree.resize(n * 4); }
//建树
void Build(vector<int> nums) { Build(1, 0, n - 1, nums); }
//区间修改
void Update(int l, int r, int val) { Update(1, 0, n - 1, l, r, val); }
//区间查询
int Sum(int l, int r) { return Sum(1, 0, n - 1, l, r); }
private:
int n;
vector<Node> tree;
void Build(int p, int s, int t, vector<int>& nums) {
if (s == t)
{
tree[p].sum = nums[s];
return;
}
int mid = (s + t) >> 1;
Build(p * 2, s, mid, nums);
Build(p * 2 + 1, mid + 1, t, nums);
PushUp(p);
}
void Update(int p, int s, int t, int l, int r, int val) {
if (s == t)
{
tree[p].sum = val * (r - l + 1);
tree[p].val = val;
tree[p].tag = true;
return;
}
int mid = (s + t) >> 1;
PushDown(p, mid - s + 1, t - mid);
if (l <= mid) Update(p * 2, s, mid, l, r, val);
if (r > mid) Update(p * 2 + 1, mid + 1, t, l, r, val);
PushUp(p);
}
int Sum(int p, int s, int t, int l, int r)
{
if (s >= l && t <= r) return tree[p].sum;
int res = 0;
int mid = (s + t) >> 1;
PushDown(p, mid - s + 1, t - mid);
if (l <= mid) res += Sum(p * 2, s, mid, l, r);
if (r > mid) res += Sum(p * 2 + 1, mid + 1, t, l, r);
return res;
}
void PushUp(int p)
{
tree[p].sum = tree[p * 2].sum + tree[p * 2 + 1].sum;
}
void PushDown(int p, int cl, int cr)
{
if (!tree[p].tag) return;
tree[p * 2].tag = tree[p * 2 + 1].tag = true;
tree[p * 2].val = tree[p * 2 + 1].val = tree[p].val;
tree[p * 2].sum = tree[p].val * cl;
tree[p * 2 + 1].sum = tree[p].val * cr;
tree[p].tag = false;
tree[p].val = 0;
}
};
//模板结束
class NumArray {
public:
SegmentTree* tree;
NumArray(vector<int>& nums) {
int n = nums.size();
tree = new SegmentTree(n);
tree->Build(nums);
}
void update(int index, int val) {
//注意这里是[index, index]的区间修改模拟单点修改
tree->Update(index, index, val);
}
int sumRange(int left, int right) {
return tree->Sum(left, right);
}
};
动态开点
现在我们考虑一个新问题,线段树的节点数组初始化长度是\(4n\),如果\(n\)非常大怎么办?
比如没有初始数组,然后区间修改的范围\([L,R]\)非常大,如1e9,显然我们创建4e9长度的数组,内存过大。还能否使用线段树处理?
解决上面问题有个通用技巧叫做离散化。假设我们已知了所有操作,操作数\(q\)是比较小的,如1e5,那么每次操作出现的不同区间\(L,R\),也是比较少的,离散分布于\([0,1e9]\)范围内。那么我们可以把这些所有的\([L,R]\)映射到\([0,1e5]\)范围内。
具体地,排序所有出现的数据,第一个数据对应1,之后每个不同的数据递增。映射完毕后,再建线段树即可。这个技巧就是离散化
离散化有一个严格的要求,就是所有的查询必须是离线的,也就是必须预先知道所有的查询数据。如果是强制在线呢?
此时我们需要使用动态开点技巧。
所谓动态开点,就是我们直到真正使用某个节点时,再创建这个节点数据,显然每个节点的左右节点也不再是简单的\(p*2\)和\(p*2+1\)。
可以使用两个数组int[] left, right 表示每个节点的左右子节点的索引,根节点依然是1,然后每次创建节点时,索引递增。
区间范围会很大,但是操作数相对较小,一般的,值域大致U=1e9,操作数m依旧是1e5左右。
整体复杂度为\(O(mlogU)\),所需数组大小大致为\(30m\)这样。
动态开点线段树堪称万金油。唯一的缺点就是常数大,有时候会被卡常。
这里给出一份梦回大佬的动态开点线段树模板 速度很快
动态开点
jiangly的模板
jiangly,当前CF第一人,用的线段树板子
参考这里
主要思路是把延迟标记,PushUp/PushDown操作,都封装到类里(jiangly模板里叫Info类,以及维护延迟标记的Tag类),这样线段树框架代码可以保持不变
每次针对题目只需要修改:
- Info类的实现
- Tag类的视线
- Info重载加法运算
非常值得借鉴。
这里按个人习惯修改下命名,然后就是我的板子了
下面同样是307. 区域和检索 - 数组可修改的完整jiangly模板代码
//jiangly segment tree
//这里只保留了区间修改,区间查询。不支持动态开点
template<class Info, class Tag>
struct SegmentTree {
#define l(p) (p << 1)
#define r(p) (p << 1 | 1)
int n;
std::vector<Info> info;
std::vector<Tag> tag;
SegmentTree() {}
SegmentTree(int _n, Info _v = Info()) { init(_n, _v); }
template<class T>
SegmentTree(std::vector<T> _init) { init(_init); }
void init(int _n, Info _v = Info()) { init(std::vector(_n, _v)); }
template<class T>
void init(std::vector<T> _init) {
n = _init.size();
info.assign(n * 4, Info());
tag.assign(n * 4, Tag());
auto build = [&](auto self, int p, int l, int r) {
if (l == r) {
info[p] = _init[l];
return;
}
int m = (l + r) >> 1;
self(self, l(p), l, m);
self(self, r(p), m + 1, r);
pushup(p);
};
build(build, 1, 0, n - 1);
}
void pushup(int p) { info[p] = info[l(p)] + info[r(p)]; }
void apply(int p, const Tag& v, int len) {
info[p].apply(v, len);
tag[p].apply(v);
}
void pushdown(int p, int len) {
apply(l(p), tag[p], (len + 1) / 2);
apply(r(p), tag[p], len / 2);
tag[p] = Tag();
}
Info query(int p, int l, int r, int x, int y) {
if (l > y or r < x) {
return Info();
}
if (l >= x and r <= y) {
return info[p];
}
int m = l + r >> 1;
pushdown(p, r - l + 1);
return query(l(p), l, m, x, y) + query(r(p), m + 1, r, x, y);
}
void update(int p, int l, int r, int x, int y, const Tag& v) {
if (l > y or r < x) {
return;
}
if (l >= x and r <= y) {
apply(p, v, r - l + 1);
return;
}
int m = l + r >> 1;
pushdown(p, r - l + 1);
update(l(p), l, m, x, y, v);
update(r(p), m + 1, r, x, y, v);
pushup(p);
}
//API 区间查询
Info Query(int l, int r) {
return query(1, 0, n - 1, l, r);
}
//API 区间修改
void Update(int l, int r, const Tag& v) {
return update(1, 0, n - 1, l, r, v);
}
#undef l(p)
#undef r(p)
};
//每次只需要修改以下三个地方。
struct Tag {
int val;
bool flag;
Tag(int _val = 0, bool _flag = false) :val(_val), flag(_flag) {}
void apply(Tag t) {
if(t.flag){
val = t.val;
flag = t.flag;
}
}
};
struct Info {
int sum = 0;
void apply(Tag t, int len) {
if (t.flag) sum = t.val * len;
}
};
inline Info operator+(Info a, Info b) {
Info c;
c.sum = a.sum + b.sum;
return c;
}
class NumArray {
public:
SegmentTree<Info, Tag>* tree;
NumArray(vector<int>& nums) {
int n = nums.size();
vector<Info> infos(n);
for (int i = 0; i < n; i++) infos[i].sum = nums[i];
tree = new SegmentTree<Info, Tag>(infos);
}
void update(int index, int val) {
tree->Update(index, index, Tag(val, true));
}
int sumRange(int left, int right) {
return tree->Query(left, right).sum;
}
};
应用
引入线段树的例子中,区间修改和区间查询对应的是区间赋值和查询区间和。
但是区间操作远不止这两种行为。还可能是各种能用线段树维护的操作,如求和,求极值,与或,或者某些自定义操作。
一般来说,满足区间结合律的操作,都可以使用线段树维护。比如
\(sum[1,5]=sum[1,3]+sum[4,5]\)
\(max[1,5]=max(max[1,3],max[4,5])\)
自定义的行为可能会更复杂。
下面介绍线段树的常见使用。
前缀和/差分/ST表/树状数组等上位替代
首先是这三类题目,线段树一定可以做,特性更完整,支持更广,缺点是复杂度更高或常数更大。
前缀和/差分/ST表的复杂度为\(O(1)\)。
树状数组的复杂度虽然也是\(O(logn)\),但是常数要比线段低很多。
特别提醒,日常训练,这些类型的题目就尽量不要使用线段树了。
线段树用多了降思维能力。
极值
699. 掉落的方块 区间修改+极值
这里我们用下jiangly的板子
//每次只需要修改以下三个地方。
struct Tag {
int val;
bool flag;
Tag(int _val = 0, bool _flag = false) :val(_val), flag(_flag) {}
void apply(Tag t) {
//如果父节点有延迟标记 则下推到子节点
if(t.flag){
val = t.val;
flag = t.flag;
}
}
};
struct Info {
int max = 0; //注意这里最小值是0 可能有些题目需要INT_MIN
void apply(Tag t, int len) {
//有延迟标记时再更新
if (t.flag) max = t.val;
}
};
inline Info operator+(Info a, Info b) {
Info c;
c.max = max(a.max, b.max); //极值的合并方式
return c;
}
class Solution {
public:
vector<int> fallingSquares(vector<vector<int>>& positions) {
//本题数据范围较大,直接建树空间过大TLE。
//一种做法是动态开点,另一种是离散化。由于数据可以离线处理,正好使用下jiangly模板。
//以下是离散化处理
set<int> set{0, (int)1e9};
for(auto& v : positions){
set.insert(v[0]);
set.insert(v[0] + v[1] - 1);
}
int n = set.size();
map<int, int> raw;
int pos = 0;
for(auto v : set) raw[v] = pos++;
//离散化结束
SegmentTree<Info, Tag> tree(n);
vector<int> ans;
for(auto& v : positions){
//由于左右边界允许紧贴,所以统一按照左闭右开查询和更新(Trick)
int L = raw[v[0]], R = raw[v[0] + v[1] - 1], H = v[1];
int mx = tree.Query(L, R).max;
mx += H;
tree.Update(L, R, Tag(mx, true));
//注意是查询整个区间的最大值 而非当前更新区域的最大值
ans.push_back(tree.Query(raw[0], raw[1e9]).max);
}
return ans;
}
};
乘法+加法
2569. 更新数组后处理求和查询
可以有别的做法,但是考虑到0-1的互换等价于 乘-1再加上1 我们实现一下同时维护乘,加,区间和查询的线段树
//每次只需要修改以下三个地方。
using i64 = long long;
struct Tag {
i64 mul;
i64 add;
bool flag;
Tag(i64 _mul = 1, i64 _add = 0, bool _flag = false) : mul(_mul), add(_add), flag(_flag) {}
void apply(Tag t) {
if(t.flag){
mul *= t.mul;
add *= t.mul;
add += t.add;
flag = true;
}
}
};
struct Info {
i64 sum;
void apply(Tag t, int len) {
if (t.flag){
sum *= t.mul;
sum += t.add * len;
}
}
};
inline Info operator+(Info a, Info b) {
Info c;
c.sum = a.sum + b.sum;
return c;
}
//具体执行乘加处理
tree.Update(v[1], v[2], Tag(-1, 1, true));
//其它略
二维偏序
这个是线段树中的经典用法,需要熟练掌握。
偏序粗略理解就是大小关系,一维偏序可类比数组里元素的大小顺序。
二维偏序意思是某个数据有两个维度\(x,y\),原数据可能是这种数据的集合,需求是查询两个维度同时满足条件的情况下的结果。
比如二维数组\(nums\) [[1,5],[2,10],[3,3],[4,1]],对于每个元素\(nums[i]\),已知整数\(x,y\),查询满足\(nums[i][0]<x\),且\(nums[i][1]<y\)的元素个数。
单次查询显然可以通过一次遍历得出结果。但是如果是多次查询呢?查询次数如果是\(m\),整体复杂度将达到\(O(nm)\),这是无法接受的。
二维偏序的通用解法是,首先对其中一个维度排序,这样当枚举时,该维度就都是有效的。而另一个维度,使用线段树维护结果,可以以\(O(logU)\)查询,其中\(U\)是该维度的最大值。
没错,对元素值建树是常用的技巧。
求数组逆序对个数其实是典型的二维偏序问题,不过其中一个维度(数组下标)已经是排序好的。
更典型的例子2736. 最大和查询
线段树优化dp
线段树本身功能强大,应用广泛,可能只是作为工具用来优化某一部分逻辑。
典型如线段树优化的动态规划。
//没有贴线段树的板子,是一个支持动态开点的模板。
class Solution {
public:
int lengthOfLIS(vector<int>& nums, int k) {
int n = nums.size();
SegmentTree tree;
for (int i = 0; i < n; i++)
{
int v = nums[i];
//要求严格递增 所以区间右边界是v-1,要求差值<=k,所以左边界是v-k
int max = (int)tree.Max(Math.Max(v - k, 0), v - 1) + 1;
int pre = (int)tree.Sum(v, v);
if (max > pre) tree.Update(v, v, max);
}
return (int)tree.Max(0, (long)1e9);
}
};
线段树二分
某些情况下需要对线段树进行二分求解,如求区间内第一个>=target的下标[0, n - 1]。
显然一种做法是二分区间,查询最大值,但是这样复杂度是\(O(nlog^2n)\)。
二分的部分写在查询内部,可以减少一个\(logn\)
3479. 将水果装入篮子 III
典型线段树二分题目
这里直接贴一个纯净版的代码,以便于理解。
class Solution {
public:
int numOfUnplacedFruits(vector<int>& fruits, vector<int>& baskets) {
int n = fruits.size();
vector<int> tree(n * 4);
auto build = [&](auto&& self, int p, int s, int t)->void{
if(s == t) {tree[p] = baskets[s]; return;}
int m = (s + t) >> 1;
self(self, p * 2, s, m);
self(self, p * 2 + 1, m + 1, t);
tree[p] = max(tree[p * 2], tree[p * 2 + 1]);
};
auto update = [&](auto&& self, int p, int s, int t, int i, int v)->void {
if(s == t) {tree[p] = v; return;}
int m = (s + t) >> 1;
if(i <= m) self(self, p * 2, s, m, i, v);
else self(self, p * 2 + 1, m + 1, t, i, v);
tree[p] = max(tree[p * 2], tree[p * 2 + 1]);
};
//二分查找 >= target 的第一个下标[0, n - 1]
auto query = [&](auto&& self, int p, int s, int t, int target)->int{
if(tree[p] < target) return t + 1;
if(s == t) return s;
int m = (s + t) >> 1;
if(tree[p * 2] >= target) return self(self, p * 2, s, m, target);
else return self(self, p * 2 + 1, m + 1, t, target);
};
build(build, 1, 0, n - 1);
int ans = 0;
for(auto v : fruits){
int pos = query(query, 1, 0, n - 1, v);
if(pos == n) ans++;
else update(update, 1, 0, n - 1, pos, 0);
}
return ans;
}
};
分治
这类问题是线段树基础应用中最有难度的部分
- 不是直观的类似求和求极值这种运算
- 非常考验对分治的理解,对线段树的理解
- 需要充分挖掘题目需求,找出合并处理
3165. 不包含相邻元素的子序列的最大和
可以先做一下 单次查询版本 198. 打家劫舍
这里大致写下合并的代码
//node节点下维护sum数组
void PushUp(Node* node) {
// --左右两个端点不选
// 可以是左区间选择右端点+右区间都不选
// 可以是左区间都不选+右区间选择左端点
// 取两者较大值
node->sum[0] = max(node->left->sum[2] + node->right->sum[0], node->left->sum[0] + node->right->sum[1]);
// --左选右不选
node->sum[1] = max(node->left->sum[3] + node->right->sum[0], node->left->sum[1] + node->right->sum[1]);
// --右选左不选
node->sum[2] = max(node->left->sum[2] + node->right->sum[2], node->left->sum[0] + node->right->sum[3]);
// --左右两个端点都可选
node->sum[3] = max(node->left->sum[1] + node->right->sum[3], node->left->sum[3] + node->right->sum[2]);
}
另一个同样经典的题目 线段树维护最大子段和
3410. 删除所有值为某个元素后的最大子数组和
对应洛谷上的题目是 P4513 小白逛公园
进阶
写不动了 简单介绍下
线段树的性能和zkw线段树
上文提到,线段树的常数较大。最近LeetCode的题目出的限制越来越大,导致很容易卡常。
开销比较高的点主要是
- 查询和更新自带的log系数,对比前缀和 ST表等单次\(O(1)\)
- 递归调用的开销,对比树状数组的非递归写法。
- 空间复杂度偏高,\(4n\)的空间开销,以及较多的节点数据
- 如果是动态开点,往往是\(O(logU)\)的系数,此时\(U=1e9\),和对应的\(O(nlogU)\)的空间
可以通过典型题目测试下自己的板子的开销。
下面几个是对性能要求较高的题目 可以用作实验。
3161. 物块放置查询
3413. 收集连续 K 个袋子可以获得的最多硬币数量
zkw线段树是一个非递归的线段树实现,要比递归线段树的性能更好一些。
可持久化线段树
配合动态开点,可以维护多个历史版本的线段树。
考虑线段树增加一个版本概念。
每次操作都可以针对某个版本进行,版本之间的数互不影响。
要处理这种情况,我们需要对每次新增版本时,增加根节点,然后操作时递归向下建立新节点(如果有必要)。
根节点本身变成一个列表,每次操作都是指定某个版本下的线段树进行操作。
注意:空间复杂度由普通线段树的\(O(n)\) 增加到\(O(nlogn)\)。
静态区间第k小 著名可持久化线段树模板题
1157. 子数组中占绝大多数的元素 LC上的一个可以用可持久化线段树解决的例子。
树套树
线段树套线段树
可以配合二维前缀和/二维差分一起理解。
区域单词查询复杂度\(O(logn*logm)\)
ps.有一种四叉树的写法 似乎复杂度会被卡成\(O(n)\)
线段树套平衡树
线段树建图
什么时候有时间了再补充


 浙公网安备 33010602011771号
浙公网安备 33010602011771号