test20181024 nan 和 test20180919 递归问题

nan

问题描述

我们有一个序列，现在他里面有三个数1,2,2。我们从第三个数开始考虑：

1. 第三个数是2，所以我们在序列后面写2个3，变成1,2,2,3,3。
2. 第四个数是3，所以我们在序列后面写3个4，变成1,2,2,3,3,4,4,4。

那么你可以看到，这个序列应该是1,2,2,3,3,4,4,4,5,5,5,6,6,6,6, …。
如果我们设一个数𝑥 最后出现的位置为𝑙𝑎𝑠𝑡(𝑥)，那么现在我希望知道𝑙𝑎𝑠𝑡(𝑙𝑎𝑠𝑡(𝑥))等于多少。

输入格式

第一行一个整数𝑇，代表数据组数。
接下来𝑇行每行一个整数𝑥。

输出格式

𝑇行，每行一个整数，代表𝑙𝑎𝑠𝑡(𝑙𝑎𝑠𝑡(𝑥)) \(\mod (10^9 + 7)\)的值。

样例输入

3
3
10
100000

样例输出

11
217
507231491

样例解释

╭︿︿︿╮
{/ o o /}
( (oo) )
︶︶︶

数据规模与约定

对于30%的数据，1 ≤ 𝑁 ≤ \(10^3\)。
对于60%的数据，1 ≤ 𝑁 ≤ \(10^6\)。
对于100%的数据，1 ≤ 𝑁 ≤ \(10^9\), 1 ≤ 𝑇 ≤ \(2 × 10^3\)。

考场做法

这道题跟原来做过的一道题一样

但是这题有多组数据，直接套用的话是\(O(T \cdot Limit)\)的，会超时。

考虑排序去重，用差分来计算。

这样时间复杂度\(O(T^2 + Lim)\)

const int INF=0x7fffffff;

const int MAXN=1e6+7,mod=1e9+7;
ll f[MAXN],lim=1e6;

const int MAXQ=2e3+7;
struct $
{
	ll n,sum;
	vector<int>id;
	bool operator<(const $&rhs)
	{
		return n<rhs.n;
	}
}q[MAXQ];
int len;
ll ans[MAXQ];

void out(int x)
{
	for(int i=0;i<q[x].id.size();++i)
		ans[q[x].id[i]]=q[x].sum;
}

int main()
{
  freopen("nan.in","r",stdin);
  freopen("nan.out","w",stdout);
	f[1]=1;
	f[2]=f[3]=2;
	f[0]=3;

	for(ll i=3;i<=lim;++i)
	{
		for(ll j=f[0]+1,jend=min(f[0]+f[i],lim);j<=jend;++j)
			f[j]=i;
		f[0]+=f[i];
	}
	
	int T=read<int>();
	for(int i=1;i<=T;++i)
	{
		int n=read<int>();
		bool fd=0;
		for(int j=1;j<i;++j) // unique
			if(q[j].n==n)
			{
				fd=1;
				q[j].id.push_back(i);
			}
		if(!fd)
		{
			q[++len].n=n;
			q[len].id.push_back(i);
		}
	}
	sort(q+1,q+len+1); // suppose q is unique
	
	int p=1;
	if(q[p].n==1)
	{
		q[p].sum=1;
		++p;
	}
	if(q[p].n==2)
	{
		q[p].sum=5-q[p-1].sum;
		++p;
	}
	
	f[0]=3;
	q[p].sum=11-q[p-1].sum;
	for(ll i=3;i<=lim&&p<=T;++i)	
	{	
		ll up=f[i]+f[0];
		ll down=f[0]+1;
		
		while(down>q[p].n)
		{
			++p;
			if(p>len)
				break;
		}
		
		if(p>len)
			break;
		
		(q[p].sum += (__int128)(min(up,q[p].n) + down) * (min(up,q[p].n) - down + 1) / 2 % mod * i % mod) %= mod;
		
		while(up>q[p].n)
		{
			down=q[p].n+1;
			++p;
			if(p>len)
				break;
			(q[p].sum += (__int128)(min(up,q[p].n) + down) * (min(up,q[p].n) - down + 1) / 2 % mod * i % mod) %= mod;
		}
		
		if(p>len)
			break;
		
		f[0]+=f[i];
	}
	
	
	out(1);
	for(int i=2;i<=len;++i)
	{
		(q[i].sum += q[i-1].sum) %= mod;
		out(i);
	}
	
	for(int i=1;i<=T;++i)
	{
		printf("%lld\n",ans[i]);
	}
//  fclose(stdin);
//  fclose(stdout);
    return 0;
}

标解

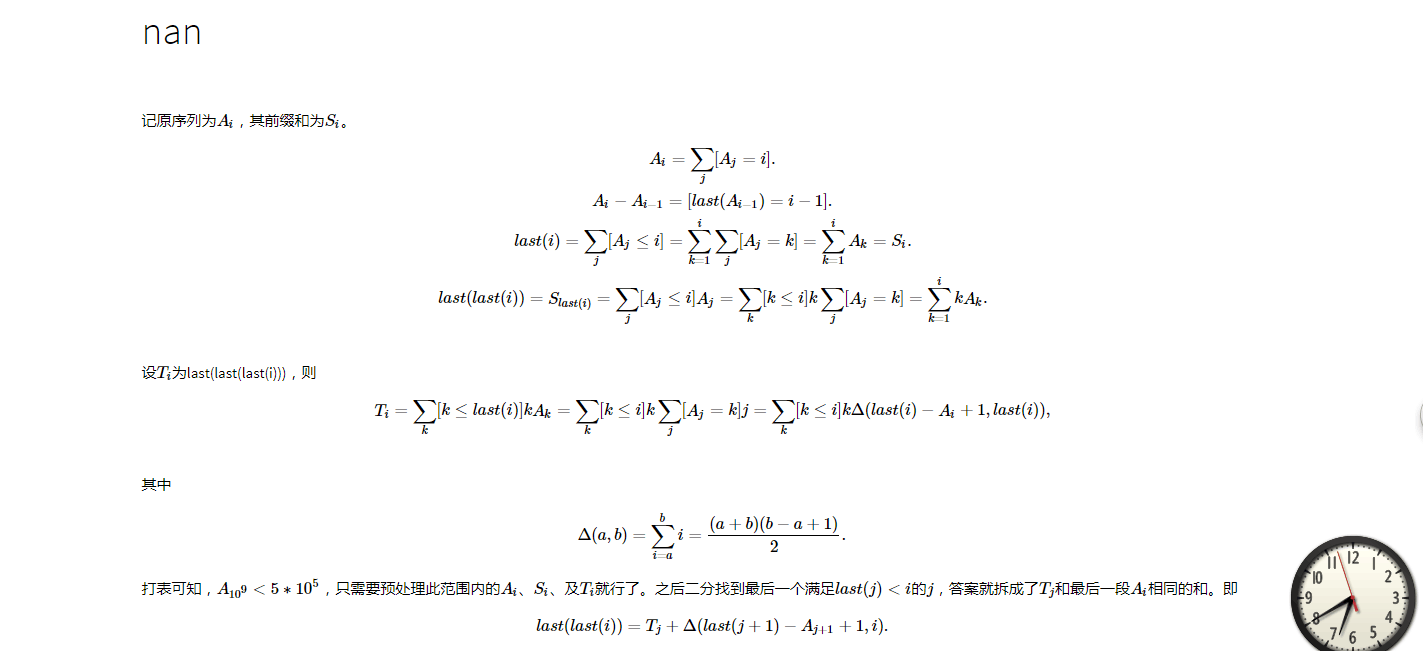
标程暂缺。

递归问题

定义

\[f(n)=\left\{ \begin{array}{} 1 & n=1\\ f(n-f(f(n-1)))+1 & n>1 \end{array} \right. \]

\(g(n)\) 为满足\(f(m) = n\)的最大的\(m\)。
给出\(n\)，求\(g(n) \mod 998244353\)，和\(g(g(n)) \mod 998244353\)。

对100%的数据，\(n \leq 10^9\)

分析

const int INF=0x7fffffff;

const ll MAXN=1e6+7,lim=1e6,mod=998244353;
ll f[MAXN]={3,1,2,2};
ll ans1=5,ans2=11;
ll n;

int main()
{
//  freopen("recursion.in","r",stdin);
//  freopen("recursion.out","w",stdout);
	read(n);
	if(n==1)
	{
		puts("1 1");
		return 0;
	}
	if(n==2)
	{
		puts("3 5");
		return 0;
	}
	for(int i=3;i<=lim;++i)
	{
		for(int j=f[0]+1;j<=min(lim,f[0]+f[i]);++j)
			f[j]=i;
		
		ll up=min(f[i]+f[0],n),down=f[0]+1;
		if(down>n)
			break;
			
		(ans1 += (ll)(up - down + 1) * i)%=mod;
		
		if((up + down)&1)
		{
			(ans2 += (up + down) % mod * (up - down + 1)/2 % mod * i) %= mod;
		}
		
		else
		{
			(ans2 += (up + down)/2 % mod * (up - down + 1) % mod * i) %= mod;
		}
		
		f[0]+=f[i];
	}
	printf("%lld %lld\n",ans1,ans2);
//  fclose(stdin);
//  fclose(stdout);
    return 0;
}