西瓜书

第1章 绪论

1.2专业术语

数据集：一组记录的集合

样本空间：
特征向量：一个示例

维数：属性个数

学习=训练：从数据中生成模型

样例：拥有标记信息的示例

标记空间：

预测：

分类：预测的是离散值的学习任务

回归：预测的是连续值的学习任务

聚类：

监督学习：分类，回归

无监督学习：聚类

泛化能力：学到的模型可用于新样本

归纳偏好：机器学习算法在学习过程中对某种类型假设的偏好

第2章 模型评估与选择

2.1 经验误差与过拟合

错误率=分类错误的样本数  /   样本总数

精度=1-错误率

训练误差，经验误差--训练集上的

泛化误差--新样本上的

欠拟合&过拟合

 

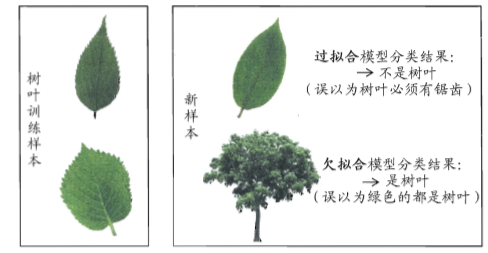
 2.2 评估方法

留出法：总样本分为训练集和测试集两部分，注意要采用若干次随机划分，返回其结果平均值

交叉验证法：分为K组（称为 K折交叉验证），（分层采样），每组大部分用于训练，小部分用于测试

 自助法：总样本D中随机生成D'作为训练集，D/D'作为测试集，

调参与最终模型

2.3性能度量

错误率与精度

查准率与查全率与F1

F1

 

2.4比较检验

假设检验

交叉验证t检验

McNemar检验

Friedman 检验和Nemenyi 检验

 

2.5偏差与方差

 

 

第3章 线性模型

3.1 基本形式

 

均方误差：

 

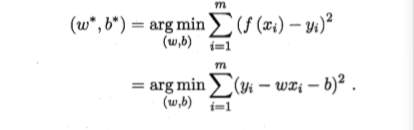
最小二乘法：基于均方误差最小的求解模型的方法

线性回归：求解w和b使得最小的过程

 若有多个属性wi ，则称为多元线性回归

对数线性回归：

3.3 对数几率回归

3.4 线性判别分析

3.5多分类学习

多分类学习---拆解---->二分类学习

3.6类别不平衡问题

不同类别训练样例数目差别很大

第4章 决策树

4.1 基本流程

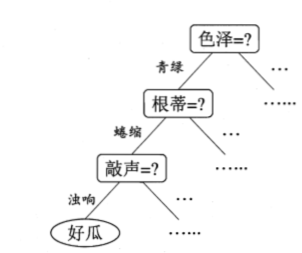
4.2划分选择

 信息增益

信息熵information entropy：度量样本集合的纯度（或者混乱度）值越大，纯度越小，值越小，纯度越大

 信息增益：

信息增益越大，使用a来进行划分所获得的纯度提升越大

决策树算法：使用增益率

增益率：

基尼指数：

 

4.3 剪枝处理

 用于决策树降低过拟合的风险

预剪枝，后剪枝

4.4 连续与缺失值