[中文翻译]JeffE Algo Ch6.5 强连通性

本文原文见: https://jeffe.cs.illinois.edu/teaching/algorithms/#book
仅作为参考.

强联通性

现在, 让我们正式地叙述在有向图中, 连通性是什么意思. 回忆: 在图\(G\)中, 如果节点\(u\)可以到达(reach)另一个节点\(v\), 并且让\(reach(u)\)表示\(u\)可以到达的所有的节点的集合. 现在我们定义: 两个节点\(u,v\)是强联通的, 当且仅当\(u\)可以到达\(v\), \(v\)可以到达\(u\). 如果这个图里面的任意两个节点都是强联通的, 我们说这个图就是强联通的.

这些繁琐的定义实际上希望做的事情是找到一个和无向图中的"连通性"类似的等价关系. 也就是说, 在图的节点上面定义这样的"强联通"的关系是一个等价关系. 这个关系的等价类被称为\(G\)的强联通分量(strongly connected components). 等价地说, \(G\)中的一个强连通分量是\(G\)中最大的联通子图. 也就是说有向图 \(G\) 是强连通的当且仅当 \(G\) 恰好有一个强联通分量. 如果我们考虑得极端一些, 如果\(G\)是有向无环图的话, 只有\(G\)剩下一个节点的时候, 这个图才是强联通的.

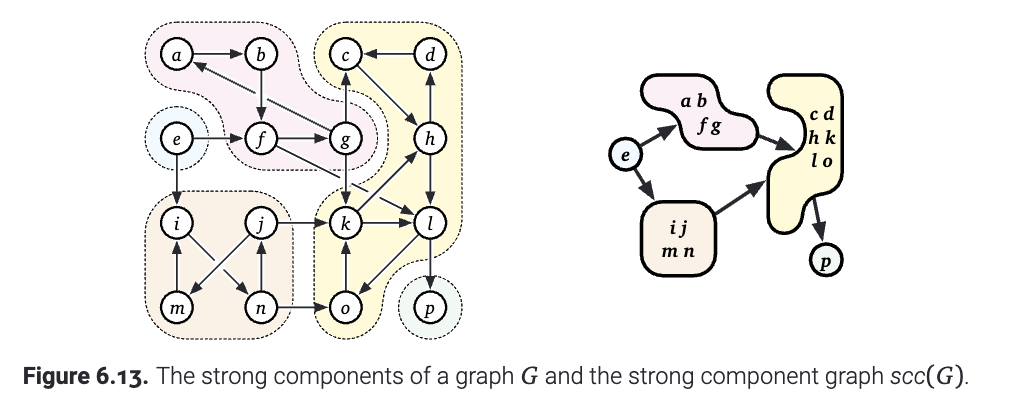
由强联通分量得到的强联通分量图(strong component graph), 通常记作\(scc(G)\), 是把\(G\)中的每一个联通分量缩成一个点, 并且只关心当前的联通分量连向其他的联通分量从而构成的一个图. (如下图) (这样的一个图有时候也叫做这个图经过缩点之后形成的). 不难证明, \(scc(G)\)肯定是一个DAG. 因此, 至少在原则上, 我们可以对 \(G\) 的强分量进行拓扑排序. 也就是说, 可以对顶点进行排序, 只要每一条回边(back edge)在同一个强联通分量里面把两个顶点连接起来.

在 \(O(V + E)\) 时间内计算单个顶点 \(v\) 的强分量很简单. 首先我们肯定能通过各种手段计算 \(reach(v)\), 然后我们通过遍历\(G\)的反图\(rev(G)\)计算\(reach\)的逆: \({reach}^{-1}(v)=\{u \mid v \in {reach}(u)\}\). 最后, \(v\)的强连通分量就是把二者相交: \({reach}(v) \cap {reach}^{-1}(v)\). 这样一来, 我们就可以在\(O(V+E)\)的时间里面确定这个图是不是强联通的了.

类似地, 我们可以用这个算法对每个点都做一次.但是, 这样一来, 算法的时间复杂度就变成了\(O(VE)\) -- 有\(V\)个联通分量, 每个都要\(E\)的时间去把它们找出来. 这个时间复杂度即使是输入图是DAG的时候也是这样! 我们当然可以做得更好, 事实上, 我们只需要\(O(V+E)\)的事件就可以决定每个节点所属于的强连通分量.