算法课程: Week 5 #2 可合并堆

1. 回顾堆

通常的堆叫做二叉堆(binary heap). 由于只有两个孩子, 可以使用数组存储. 并且兄弟之间没有关系. 这是几乎完全的二叉树.

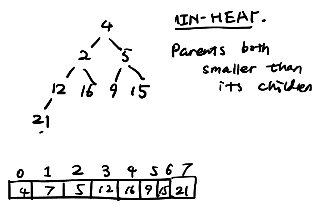
问题: 需要合并两个最小堆. 如何办?

想法1. 把一个往另一个里面合并. 需要\(O(m\log (m+n))\)的时间复杂度.

观察: 一个堆不一定要是二叉的. 因为兄弟之间没有关系. 如我们可以搞一个三叉堆.

对比三叉堆(tenary heap)和二叉堆:

• 更少的深度
• 但是更多的判别.

我们在接下来介绍可合并堆. 分别是这篇文章的二项堆(Binomial heap), 以及下一节的Fibonacci堆.

2. Binomial Heap

总的来看, Binomial heap是由若干个Binomial Tree的通过链表串联起来的. 因此我们先介绍Binomial Tree.

Binomial Tree的定义:

• \(B_{-1}\)为空, \(B_0\)由一个节点构成. \(B_1\)的左孩子为\(B_{-1}\), 右孩子为\(B_0\).
• \(B_k\)的左孩子为\(B_{k-2}\), 右孩子为\(B_{k-1}\).

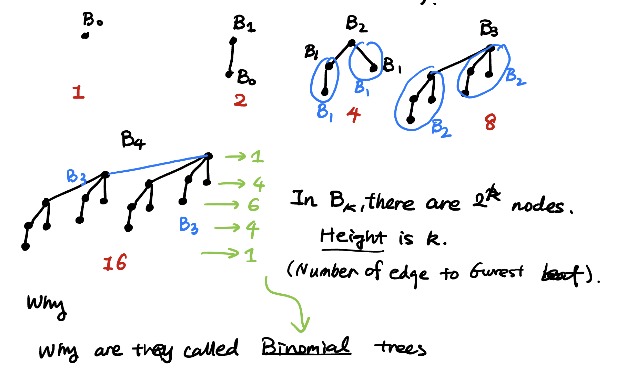
由于在第\(i\)行就像是二项式系数(Binomial Coefficient)一样, 因此叫做Binomial tree.

这使得合并两个相同大小的堆很简单.

Binomial Heap的结构:

• 这是一系列由Binomial Tree由链表串起来的数据结构.
• 每个Binomial Tree中, 都是按照堆的大小关系进行排列的.
  • 每个节点大于或等于它的父亲

接下来的情节: 可以与上一节中的数二进制(counting in binary)的例子对比. 只不过这里的"进位"是把堆去进行合并操作. 这就是我们定义了那样的一个诡异的不平衡的树的原因: 接下来的合并工作会很轻松.

接下来是一些常见操作.

make-heap: 制造一个\(B_0\)的节点即可. 时间复杂度\(O(1)\).

Insert:

• (1)把一个新的\(B_0\)放在链表的前面
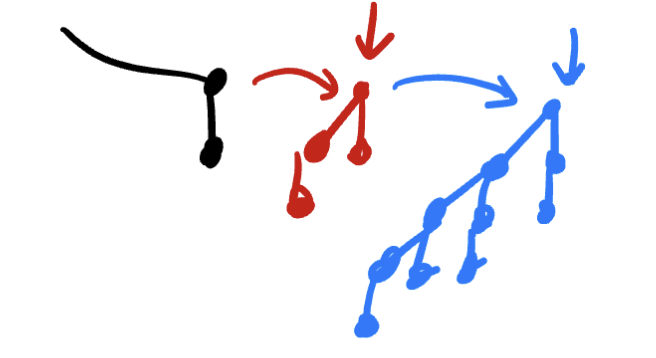
• (2)从0开始, 看邻居, 如果是一个大小的, 那么把它们合并, 得到一个\(B_1\).
  • (2.1)持续这样做. 接着遍历每一个元素, 把每两个相同\(B_k\)的合并(见下面的一个)为一个\(B_{k+1}\)的.

注意我们的链表按照Binary Heap的大小排序, 而非顶上的数字.

Union:

• (1)创建一个新的head
• (2)开两个指针\(i,j\)分别指着两个老堆的头. 选择小的加入并且合并. 直到\(i,j\)把所有的老节点遍历完.

我们每次选择小的加入是合理的, 因为我们不可能有两个重复的在每一个堆中. 因此不可能有三个连在一起.

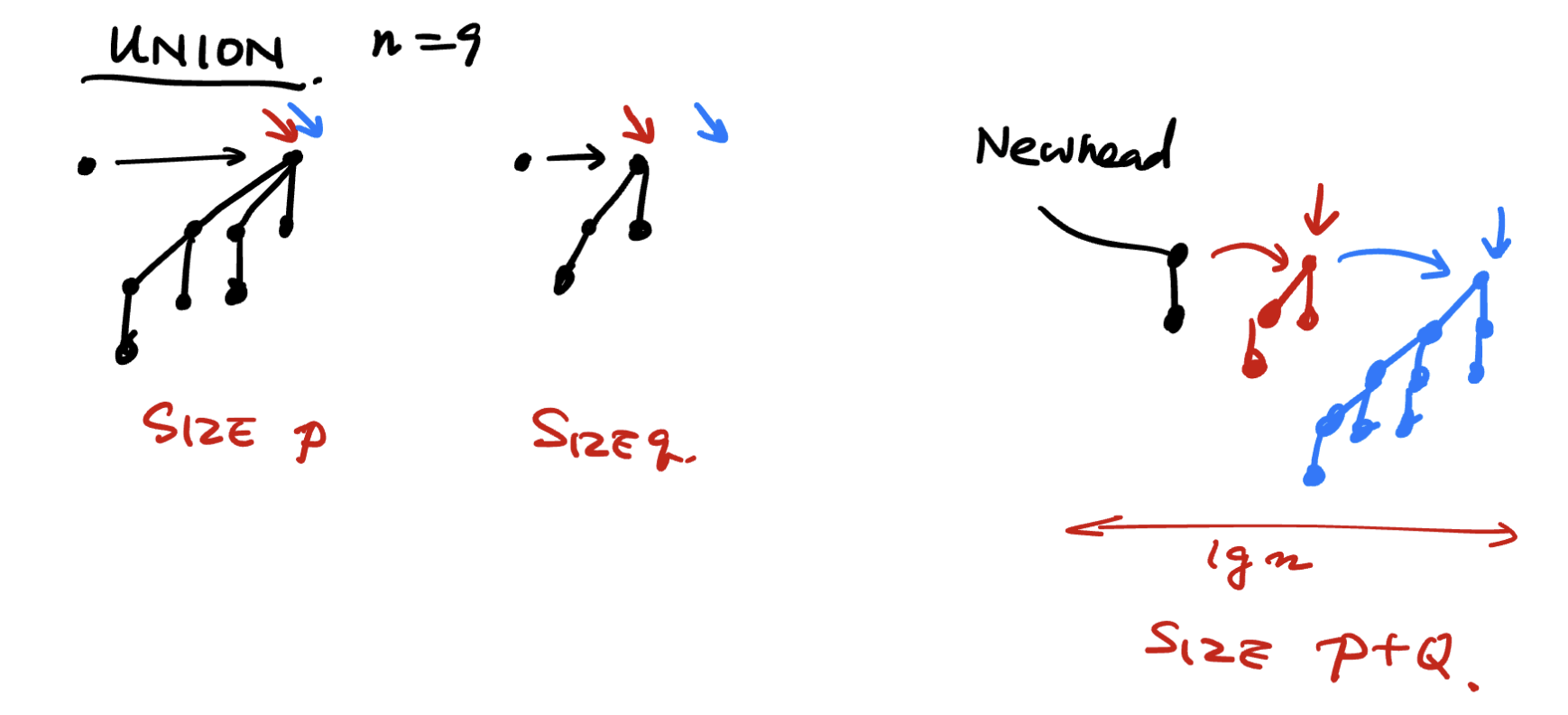
Minium: 由于列表的大小为\(\lg n\), 因此我们最多花费\(O(\lg n)\)的时间找到最小值.

Extract-Min:

• (1) 遍历根节点, 找到最小值的位置 -- \(O(\lg n)\)
• (2) 移除那个节点, 把它的孩子按照大小放回那个链表中. (这时候可能有三个在一起的情况, 但也仅仅有三个在一起的情况.)
• (3) 继续看他们的邻居, 合并他们. -- \(O(\lg n)\)

Decrease-Key

• (1) 找到这个值, 然后把它往堆上面浮动.

注意: 如何找到这个值: 可以开一个指针指着这里. 分别用AVL-tree维护大小, 以及堆来维护操作.

Delete

• 可以Decrease-Key到负无穷然后Extract-Min.