算法课程 Week 5. #3. Fibonacci堆

在上一节中我们看到了可合并堆的样子. 这次我们看一个均摊意义更高效的算法. Fibonacci堆.

1. 本节的操作和目标

实现的操作: Insert, Remove-Min, Union使用\(O(1)\)的时间.

方法: 实现一个"懒"的Binomial Heap. 直到最后的时候才合并. 如Deletion, Extract-Min. 并且删除的时候我们也不直接把它打散重组, 而是到了特定的时候才打散重组.

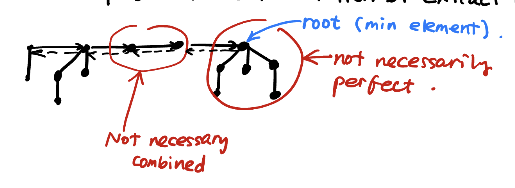
除此之外, 我们还:

• 有一系列以Min-Heap排序的一些树.
• 保持一个指针, 指向当前最小的元素.
• 如果当前的树中间缺失元素, 那么就标记这个点.

2. 常见操作

Make-Heap. 创建一个\(B_0\), 以及对应的值. 把最小值的指针指向他. 花费时间为\(O(1)\).

Insert. 把当前的内容加在当前最小节点的左边. 如果这个节点的值比原来还要小, 让这个指针指着他表示这是最小值. 时间复杂度\(O(1)\).

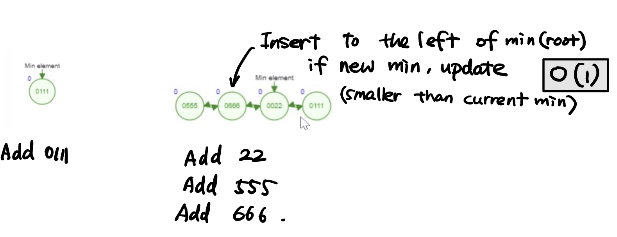
Minium: 返回当前指着的这个节点就行了. 时间复杂度\(O(1)\).

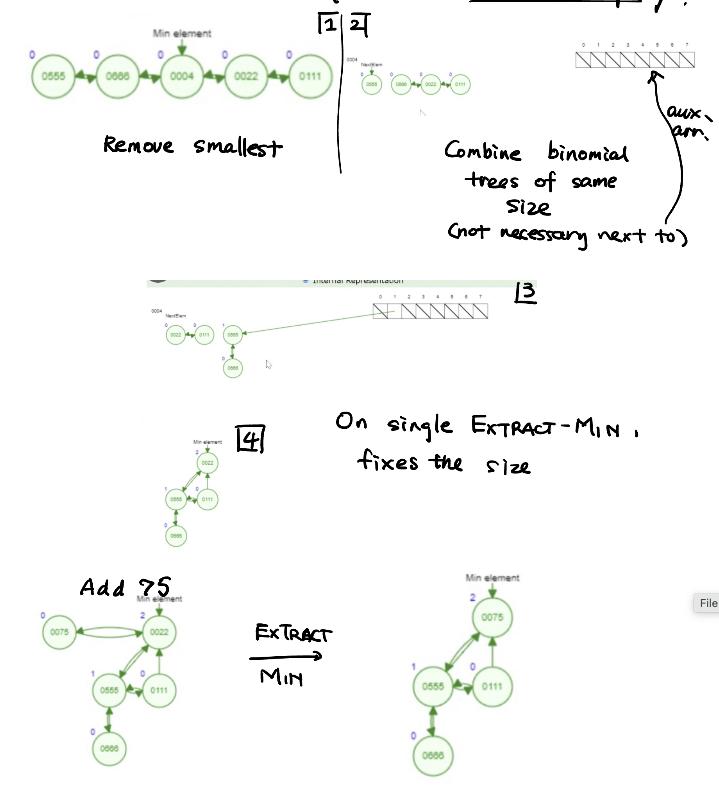
Extract-Min:

• (1) 移除最小的那一个
• (2) 开一个bit vector, 第\(i\)位表示当前有没有长度为\(i\)的树.
  • (2.1) 从左到右扫描, 通过辅助数组合并相等大小的堆.
    • (2.1.1) 获得当前的树的大小\(k\).
    • (2.1.2) 如果当前第\(k\)位为0, 把这一位指向这里. 跳到(3)
    • (2.1.3) 否则, 把它们合并, 置\(k:=k+1\), 回到(2.1.2)
• (3) 把min指针指向沿途中发现的最小的元素.

这个时间复杂度均摊下来为\(O(\lg n)\).

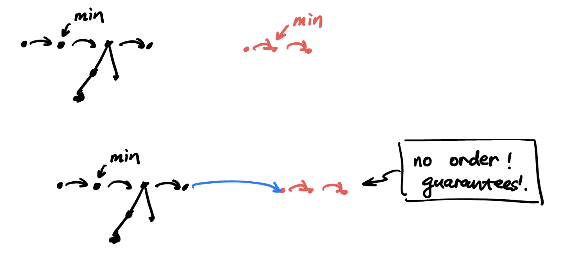
Union. 简单地把两个数拼接起来就行了. min指针选取两个中的小者.

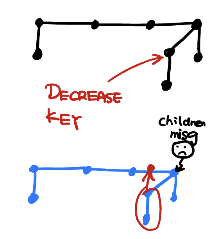
Decrease-Key.
一个Naive的想法: 还是像上次一样找到堆中的元素, 然后让这个元素walk it up就行了.

• 问题: 时间复杂度太高. 需要懒一点. (证明见算法导论)

我们使用如下的策略:

• 如果要decrease的key还要比parent大, 我们做完了!
• 如果要decreased的key不比parent大, 那么把它放到root list上面, 并且把它的parent标记为missing.
• 如果要移动一个节点, 这个节点已经被标记为missing了, 拆开做修改.
  

也就是当失去第二个孩子的时候我们才做修改. 下面是一个例子:

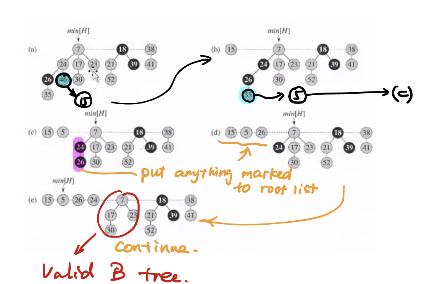
这使得我们的操作摊还下来是\(O(1)\)的时间复杂度.

delete: 先Decrease-Key在Extract-Min.