LeetCode日记——【数据结构】图专题(大坑未完结)
预备知识
邻接表:
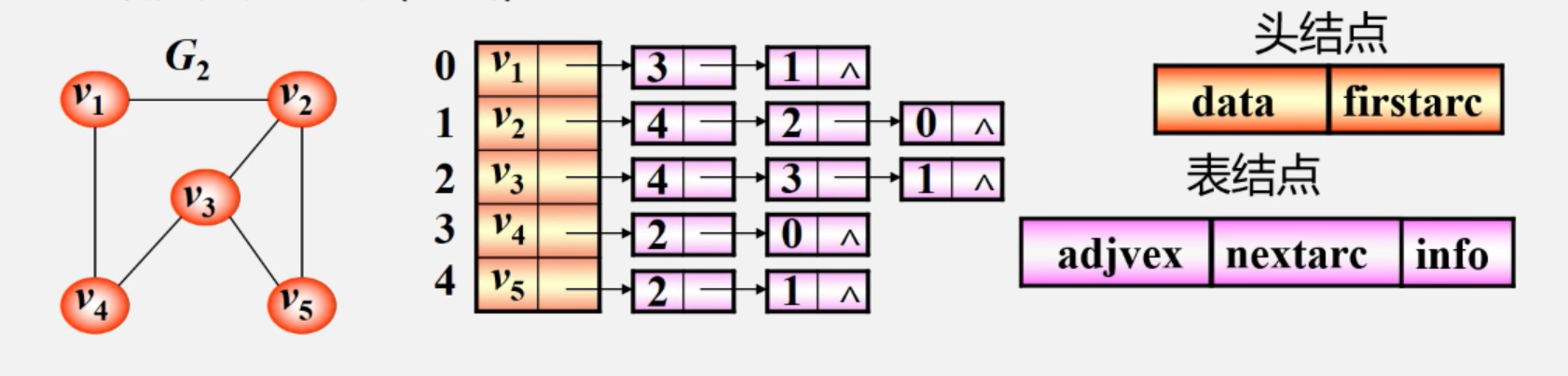
头节点表示图中的各个顶点。每个头节点后面都跟着若干个表节点,表示与该顶点相连的各边。每个表节点都存储着与之相连的顶点的索引(从0开始编号)。
度:与顶点相连的边数
入度&出度:有向图中指向该节点的边数/该顶点指向的边数
有向无圈图&有向有圈图
题1:判断二分图
难度:Medium
题目描述:
给定一个无向图graph,当这个图为二分图时返回true。
如果我们能将一个图的节点集合分割成两个独立的子集A和B,并使图中的每一条边的两个节点一个来自A集合,一个来自B集合,我们就将这个图称为二分图。
graph将会以邻接表方式给出,graph[i]表示图中与节点i相连的所有节点。每个节点都是一个在0到graph.length-1之间的整数。这图中没有自环和平行边: graph[i] 中不存在i,并且graph[i]中没有重复的值。
代码:
1 class Solution { 2 public boolean isBipartite(int[][] graph) { 3 int[] colors = new int[graph.length]; 4 Arrays.fill(colors, -1); 5 for (int i = 0; i < graph.length; i++) { // 处理图不是连通的情况 6 if (colors[i] == -1 && !isBipartite(i, 0, colors, graph)) { 7 return false; 8 } 9 } 10 return true; 11 } 12 13 private boolean isBipartite(int curNode, int curColor, int[] colors, int[][] graph) { 14 //-1表示未涂色,若已被涂色,先判断涂的颜色是否等于应该被涂的颜色 15 if (colors[curNode] != -1) { 16 return colors[curNode] == curColor; 17 } 18 //给当前节点涂色 19 colors[curNode] = curColor; 20 //给当前节点所连接的其他节点涂色 21 for (int nextNode : graph[curNode]) { 22 if (!isBipartite(nextNode, 1 - curColor, colors, graph)) { 23 return false; 24 } 25 } 26 return true; 27 } 28 }
分析:
图的DFS&BFS可以参考这里,这个小哥哥讲的很好,声音超好听~
这道题的解答过程我看的这里,但是事实上还是没有完全搞懂......
预备知识:拓扑排序
这个视频讲的很清楚,一看就明白了,感谢王卓老师!!
只有有向无环图(DAG图)可以进行拓扑排序。
拓扑排序需要用到AOV网的概念:
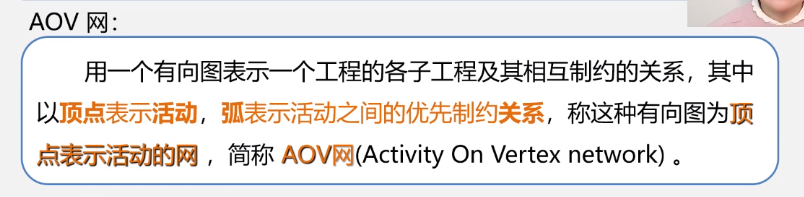
用一个经典的例子来介绍拓扑排序:
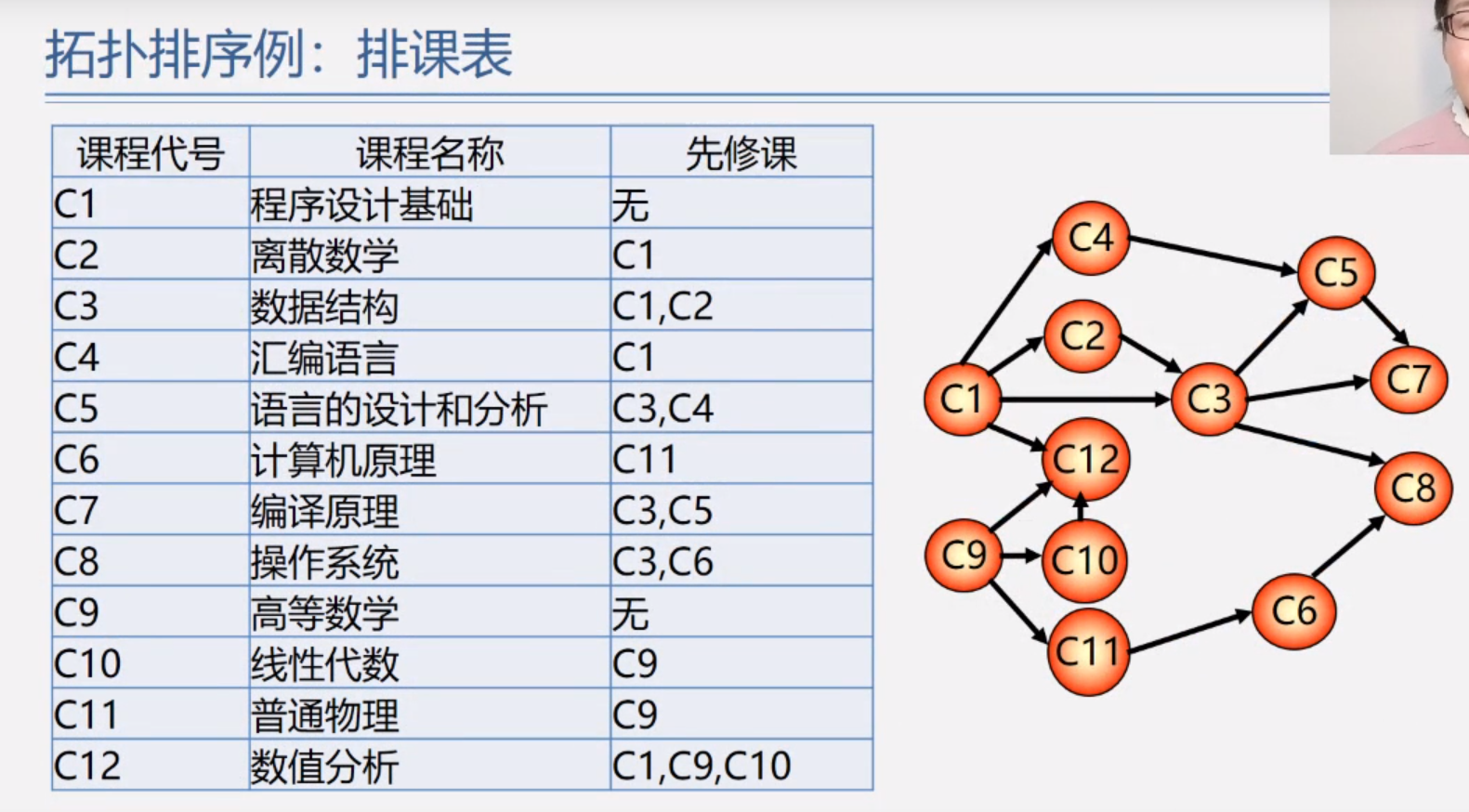
各个课程之间的修习过程可以用一个有向无环图来表示。
那么到底什么是拓扑排序呢??
拓扑排序的定义:

通俗地说就是,根据这些课程有向无环图,把这些课程排一个线性的上课顺序,这个顺序要满足各个课程的修习先后过程。
那么具体怎么实现呢??

如果这个图中有环,那么必定有顶点不能输出,因为环中的每个顶点不可能没有前驱。
好了,现在开始做题!!
题2:课程表
难度:Medium
题目描述:
你这个学期必须选修 numCourse 门课程,记为 0 到 numCourse-1 。
在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们:[0,1]
给定课程总量以及它们的先决条件,请你判断是否可能完成所有课程的学习?
示例 :
输入: 2, [[1,0]]
输出: true
解释: 总共有 2 门课程。学习课程 1 之前,你需要完成课程 0。所以这是可能的。
示例 2:
输入: 2, [[1,0],[0,1]]
输出: false
解释: 总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0;并且学习课程 0 之前,你还应先完成课程 1。这是不可能的。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号